All but two of the stages along the cache's critical path can be approximated by simple first-order stages as in the previous section. The bitline and comparator equivalent circuits, however, require more complex solutions. Figure 10 shows an equivalent circuit that can be used for the bitline and comparator circuits. From [5], the delay of this circuit can be written as:
where 
is the voltage at the beginning of the transistion, and
is the voltage at which the stage is considered to have
``switched'' ( 
). For the comparator, is 
and
is the threshold voltage of the multiplexor driver.
For the bitline subcircuit, is the precharged voltage of
the bitlines ( 
), and is the voltage which causes the sense
amplifier output to fully switch ( 
).
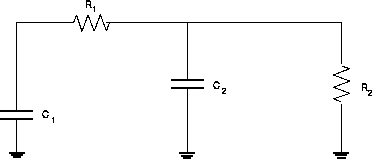
Figure 10: Equivalent circuit for bitline and comparator
When estimating the bitline delay, a non-zero wordline rise time is taken
into account as follows. Figure 11 shows the wordline voltage
as a function of time for a step input. The time difference 
shown on the graph is the time after the input rises
(assuming a step input) until the output reaches
(the output voltage is not shown on the graph).
An equation for is given above. During this time,
we can consider the bitline being ``driven'' low.
Because the current sourced by the
access transistor can be approximated as
the shaded area in the graph can be thought of as the amount of
charge discharged before the output reaches
.
This area can be calculated as:
( 
is the voltage at which the NMOS transistor begins to conduct).
If we assume that the same amount of ``drive'' is required to drive
the output to regardless of the shape
of the input waveform, then we can calculate the output delay
for an arbitrary input waveform.
Consider Figure 12-a.
If we assume the area is the same as in Figure 11,
then we can calculate the value of T (delay adjusted for input rise time).
Using simple algebra, it is easy to show that
where m is the slope of the input waveform (this can be estimated using
the delay of the previous stage). Note that the bitline delay is measured
from the time the wordline reaches . Unlike the version of the model
described in [3], the wordline rise time in this model is
defined as the time until the bitlines begin to discharge; this happens when
the wordline reaches .
Figure 12: Non-zero input rise time
If the wordline rises quickly, as shown in Figure 12-b, then the algebra is slightly different. In this case,
The cross-over point between the two cases for T occurs when:
The non-zero input rise time of the comparator can be taken into account
similarly. The delay of the comparator is composed of two parts: the delay
of the timing chain and the delay discharging the output (see
Figure 5). The delay of the first three inverters in the
timing chain can be approximated using simple first-order RC stages as
described in Section 5.5. The time to discharge the
comparator output through the final inverter can be estimated using the
equivalent circuit of Figure 10 and taking into account the
non-zero input rise time using the same technique that was used for the
bitline subcircuit. In this case, the ``input'' is the output of the third
inverter in the timing chain (we assume the timing chain is long enough that
the 
and 
lines are stable). The discharging delay of the
comparator output is measured from the time the input reaches the threshold
voltage of the final timing chain inverter. The equations for this case can
be found in [3].
