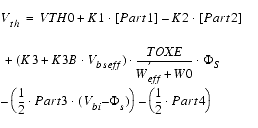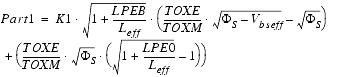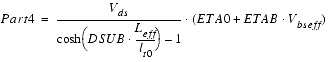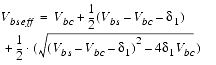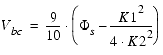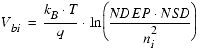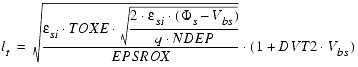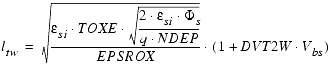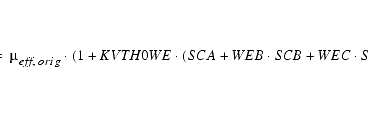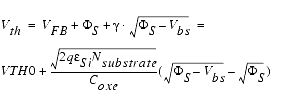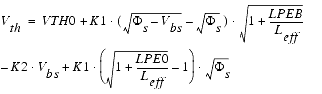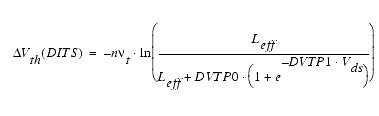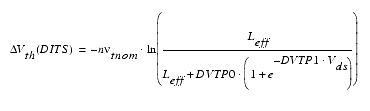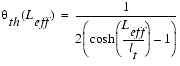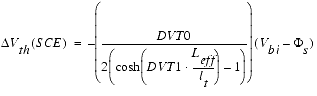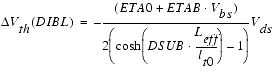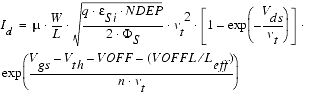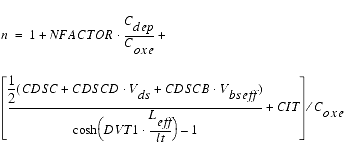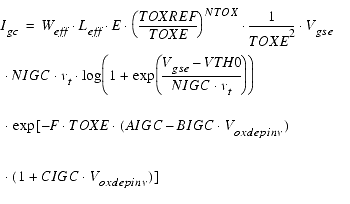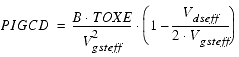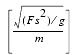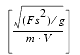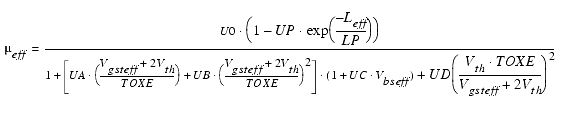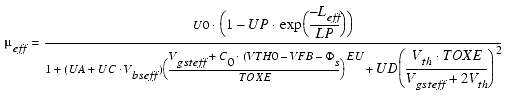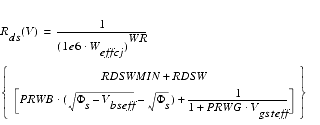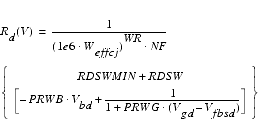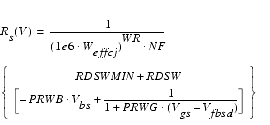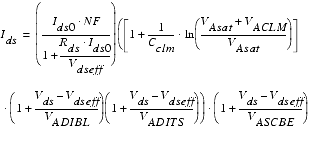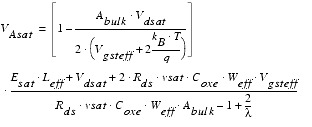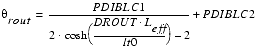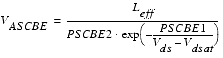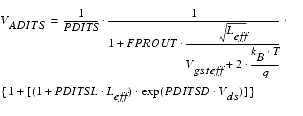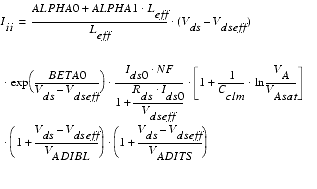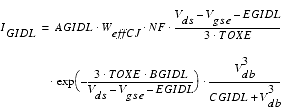DC Behavioral Modeling

This section provides a theoretical background of the BSIM4 DC model. You will find some basic device equations together with some explanations on model selectors used inside the BSIM4 model and the BSIM4 Modeling Package.

At the end of this section you will find a table listing all of the model parameters added in BSIM4.3.0 together with their default values as well as a table containing the parameter set used in version BSIM4.2.1.

Since this theoretical section can only be of introductional character, we strongly recommend that you consult the manual from the University of California, Berkeley for a detailed description of device equations and relevant parameters [1] as well as further literature located in References.

Threshold Voltage Model

The complete threshold voltage model equation implemented in the BSIM4 model for SPICE is (the influence of the well-proximity effect is described at the end of this paragraph):

(4)

The equation above contains some shortcuts for better readability ( ). Expanded they read:

To set an upper boundary for body bias during simulations, the effective body bias has been introduced:

(5)

where and is the maximum allowable

and is calculated from to be

Furthermore, there are some shortcuts used to make Equation 4 more readable.

- built-in voltage of the Source/Drain regions:

- characteristic length :

and

- effective channel length and width, and :

Well-Proximity effect modeling

With BSIM4.5.0, the calculation of influences from the so called well-proximity has been introduced. Deep buried layers, possible by using high-energy implanters, affect devices located near the mask edge. Ions, scattered at the edge of the photo resist film, can influence the threshold voltage of those edge devices. A threshold voltage shift in the order of around 100 mV have been observed [1]. The following figure shows the effect [7].

BSIM4.5.0 considers the variations of threshold voltage, mobility, and body effect through newly introduced parameters SCA, SCB, SCC, SC, WEB, WEC, KVTH0WE, K2WE, KU0WE, SCREF, and WPEMOD.

The relevant model equations are:

Table 36 Variables and parameters used in modeling threshold voltage 

Equation Variable	BSIM4 Parameter	Description	Default Value
VTH0	VTH0	long channel threshold voltage at Vbs = 0	NMOS: 0.7 V PMOS: -0.7 V
K1	K1	first-order body effect coefficient	0.5
K2	K2	second-order body effect coefficient	0
K3	K3	narrow width coefficient	80.0
K3B	K3B	Body effect coefficient of K3	0.0 1/ V
W0	W0	narrow width parameter	2.5E-6 m
LPE0	LPE0	lateral non-uniform doping parameter at Vbs = 0	1.74e-7
LPEB	LPEB	lateral non-uniform doping effect on K1	0 V
kB		Boltzmann's constant ( )
T	T	absolute temperature in Kelvin	300
q		charge of an Electron (
Ldrawn	-	channel length as drawn on mask	-
Wdrawn	-	channel width as drawn on mask	-
NF	NF	number of gate fingers	1
TOXE	TOXE	electrical gate equivalent oxide thickness	3E-9m
TOXM	TOXM	Gate oxide thickness at which parameters are extracted	TOXE
DVT0	DVT0	first coefficient of short-channel effect on VTH	2.2
DVT0W	DVT0W	first coefficient of narrow-width effect on VTH for small channel length	0
DVT1	DVT1	second coefficient of short-channel effect on VTH	0.53
DVT1W	DVT1W	second coefficient of narrow-width effect on VTH for small channel length	5.3E6m
DVT2	DVT2	body-bias coefficient of short-channel effect on VTH	-0.032 1/V
DVT2W	DVT2W	body-bias coefficient of narrow-width effect on VTH for small channel length	-0.032 1/V
DSUB	DSUB	DIBL coefficient exponent in subthreshold region	DROUT
ETA0	ETA0	DIBL coefficient in the subthreshold region	0.08
ETAB	ETAB	body-bias for the subthreshold DIBL effect	-0.07 1/V
NDEP	NDEP	channel doping concentration at , the depletion edge at	1E17 cm-3
NSD	NSD	doping concentration of the S/D diffusions	1e20 cm-3
		relative dielectric constant of silicon	11.8
EPSROX	EPSROX	gate isolators relative dielectric constant (silicon dioxide)	3.9
		surface potential	-
Vbs		Bulk-Source voltage	-
Vds		Drain-Source voltage	-

The following sections provide equations for effects modeled in the complete equation above, Equation 4. Starting from the basic equation for long and wide channels, the effects of shrinking dimensions and substrate doping variations are modeled step by step.

Basic Threshold voltage equation

For long and wide channels the following equation is valid:

(6)

Equation 6 is valid under the following assumptions:

Model parameters used for the equation above are listed in the table below:

Table 37 BSIM4 model parameters used in the basic threshold voltage equation

Equation Variable	BSIM4 Parameter	Description	Default Value
	GAMMA	body bias coefficient
Nsubstrate	NSUB	uniform substrate doping concentration	6E16 cm-3
Coxe
VFB	VFB	flatband voltage	-1.0 V

If the substrate doping is not constant or if the channel is short and/or narrow, the basic equation should be modified. The following sections show modifications to the basic equation for non-uniform doping concentration and for short or narrow channel effects.

Non-Uniform Substrate Doping

If the substrate doping concentration is not uniform in vertical direction, the body bias coefficient is a function of the substrate bias and the depth from the interface. The threshold voltage in case of non-uniform vertical doping is:

(7)

where

The doping profile is assumed to be a steep retrograde and is approximated in BSIM4. For details on how it is modeled, see the manual from UC Berkeley [1] starting on page 2-2. The model parameters K1 and K2 can be calculated from NSUB, XT, VBX, VBM, and so on. This is done the same way as in BSIM3v3. Details can be found on page 2-4 of the BSIM4 manual.

Table 38 Non-uniform substrate doping model parameters

Equation Variable	BSIM4 Parameter	Description	Default Value
ni		intrinsic carrier concentration in the channel region
PHIN	PHIN	Non-uniform vertical doping effect on surface potential	0.0

Non-Uniform Lateral Doping: Pocket or Halo Implant

The doping concentration in this case varies from the middle of the channel towards the source/drain junctions. Shorter channel lengths will result in a roll-up of from the rise of the effective channel doping concentration and the changes of the body bias effect. Those effects are considered using the following formulation:

(8)

Additionally, drain-induced threshold shift (DITS) has to be considered in long-channel devices using pocket implant. For in a range of interest, a simplified threshold voltage shift caused by DITS was implemented:

(9)

Using TEMPMOD=2, this formula changes to

(10)

Short-Channel and Drain-Induced-Barrier-Lowering (DIBL) Effects

For shorter channels, the threshold voltage is more sensitive to drain bias (DIBL effect) and less sensitive to body bias because of reduced control of the depletion region.

The short channel effect coefficient is given by

In BSIM3v3 this equation is approximated, which results in a phantom second roll-up when Leff becomes very small. To avoid this effect, the exact formulation is used in BSIM4. Model flexibility is increased for different technologies with additional parameters introduced and the short-channel and drain-induced-barrier-lowering effects are modeled separately.

This leads to a short-channel effect coefficient of the form:

and a variation of Vth due to the short-channel effect of:

(11)

Drain-induced barrier lowering is modeled the same way, the threshold voltage shift due to DIBL is calculated as:

(12)

DVT1 is basically equal to 1/(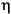)^1/2, ETAB and DVT2 represent the influence of substrate bias effects on SCE and DIBL.

Narrow-Width Effect

The existence of fringing fields leads to a depletion region in the channel that is always larger as is calculated using one-dimensional analysis. This effect gains more influence with decreasing channel widths since the depletion region underneath the fringing field becomes comparable to the depletion field formed in vertical direction. The result is an increase of Vth.

The formulation for the narrow-width effect is:

(13)

Subthreshold Swing

In the subthreshold region, the drain current flow is modeled by:

(14)

where is the thermal voltage.

The expression represents the offset voltage and

gives the channel current at .

The subthreshold swing parameter n is determined by channel length and interface state density and is calculated using

(15)

The parameter NFACTOR is used to compensate for errors in calculating the depletion width capacitance.

Table 39 Subthreshold swing parameters

Equation Variable	BSIM4 Parameter	Description	Default Value
W	W	channel width	0.25E-6
L	L	channel length	5E-6
		carrier mobility	cm²/Vsec
VOFF	VOFF	Offset voltage in subthreshold region for large W and L	-0.08 mV
VOFFL	VOFFL	Channel length dependence of VOFF	0 V
NFACTOR	NFACTOR	Subthreshold swing factor	1.0
CIT	CIT	Interface trap capacitance	0 F/m2
CDSC	CDSC	Drain-Source to channel coupling capacitance	2.4E-4 F/m2
CDSCB	CDSCB	Body-bias coefficient of CDSC	0 F/Vm2
CDSCD	CDSCD	Drain-bias coefficient of CDSC	0 F/Vm2
Cdep		depletion capacitance

Gate Direct Tunneling Current Model

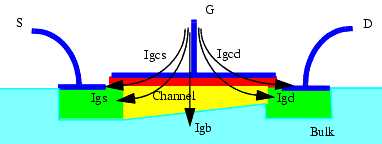
Gate oxide thickness is decreasing, therefore tunneling currents from the gate contact are playing an important role in the modeling of sub micrometer MOSFET's. In BSIM4, the gate current consists of one part tunneling from gate to bulk (Igb) and one part tunneling from gate to channel (Igc). The latter one again is partitioned to flow to the source contact (Igcs) and to the drain contact (Igcd), as well as from the gate to the source and drain diffusion regions (Igs, Igd), as is shown in the following figure.

Figure 58 Cross section of a MOSFET with gate tunneling current components

Two model selectors are used to turn on or off tunneling current components, IGBMOD and IGCMOD. Setting IGBMOD = 1 turns on Igb, IGCMOD = 1 turns on Igc, Igs and Igd. Setting IGBMOB = IBGCMOD = 0 turns off modeling of gate tunneling currents.

The BSIM4.3.0 Version of the model allows the modeling of Gate Current Tunneling through Multiple-Layer Stacks by use of a tunneling attenuation coefficient.

Gate-to-Bulk Current

This current consists of two parts, tunneling of electrons from the conduction band and from the valence band. The first part is significant in the accumulation region, the second one during device inversion. The accumulation region tunneling current is dominated by electron tunneling from the conduction band and is given by:

(16)

Inside this equation, the auxiliary voltage is:

(17)

The constants in this equation are:

A = 4.97232E-7 A/V²

B = 7.45669E11 (g/F-s²)^0.5

The tunneling current dominating the inversion region is caused by electron tunneling from the valence band. It is calculated by:

(18)

Inside this equation, the auxiliary voltage is:

The constants in the above equation are:

C= 3.75956E-7 A/V²

D= 9.82222E11 (g/F-s²)^0.5

The voltage across the gate oxide Vox consists of the oxide voltage in accumulation and the one in inversion, as used in Equation 17 and Equation 18.

(19)

The parts of Vox are calculated by:

The flatband voltage, calculated from zero-bias Vth is:

Equation 19 is continuously valid from accumulation through depletion to inversion.

Table 40 Gate Tunneling Parameters 

Equation Variable	BSIM4 Parameter	Description	Default Value
TOXREF	TOXREF	Nominal gate oxide thickness for gate direct tunneling model	3E-9 m
NTOX	NTOX	Exponent for the gate oxide ratio	1.0
AIGBACC	AIGBACC	Parameter for Igb in accumulation	0.43
BIGBACC	BIGBACC	Parameter for Igb in accumulation	0.054
CIGBACC	CIGBACC	Parameter for Igb in accumulation	0.075
NIGBACC	NIGBACC	Parameter for Igb in accumulation	1.0
AIGBINV	AIGBINV	Parameter for Igb in inversion	0.35
BIGBINV	BIGBINV	Parameter for Igb in inversion	0.03
CIGBINV	CIGBINV	Parameter for Igb in inversion	0.006
NIGBINV	NIGBINV	Parameter for Igb in inversion	1.1

Gate-to-Channel Current Igc

The gate-to-channel current is determined by electrons tunneling from the conduction band in NMOS transistors respective holes tunneling from the valence band in PMOS transistors.

(20)

The physical constants E and F are listed in Table 41.

Gate-to-Source and Gate-to-Drain tunneling currents

These currents tunnel from the gate contact to the source or drain diffusion regions. They are caused by electron tunneling from the conduction band in NMOS transistors and by hole tunneling from the valence band in PMOS transistors.

(21)

For the computing of Igd, the values of Vgs in Equation 21 has to be replaced by Vgd.

The flat-band voltage between and the source or drain diffusion areas is dependent from NGATE:

If NGATE >0.0:

Else:

To take drain bias effects into account, the tunneling current from the gate contact splits into two components and it is . The components are calculated as:

If the model parameter PIGCD is not specified, it is calculated by:

(22)

The constants used in Equation 21 and Equation 22 have different values for NMOS and PMOS transistors:

Table 41 Values of constants for gate-channel and gate S/D tunneling

	NMOS	PMOS
E	4.97232 A/V²	3.42537 A/V²
F	7.45669E11	1.16645E12

Table 42 Gate Tunneling Parameters (continued from Table 40)

Equation Variable	BSIM4 Parameter	Description	Default Value
DLCIG	DLCIG	Source/Drain overlap length for Igs and Igd	LINT
POXEDGE	POXEDGE	Factor for gate oxide thickness in source/drain overlap regions	1.0
AIGSD	AIGSD	Parameter for Igs and Igd	NMOS: 0.43 PMOS: 0.31
BIGSD	BIGSD	Parameter for Igs and Igd	NMOS: 0.054 PMOS: 0.024
CIGSD	CIGSD	Parameter for Igs and Igd	NMOS: 0.075 PMOS: 0.03 [V]
NIGC	NIGC	Parameter for Igcs, Igcd, Igs and Igd	1.0
PIGCD	PIGCD	Vgs dependence of Igcs and Igcd	1.0

Drain Current Model

Bulk Charge

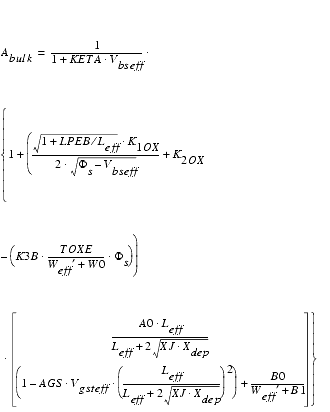
If a drain-source voltage other than zero volts is applied, the depletion width along the channel will not be uniform. Therefore, the threshold voltage VTH will vary along the channel. This phenomenon is known as the Bulk Charge Effect. Inside BSIM4, the bulk charge effect is formulated as follows:

(23)

Table 43 Drain Current Parameters 

Equation Variable	BSIM4 Parameter	Description	Default Value
Abulk		Bulk charge effect
A0	A0	Bulk charge effect coefficient	1.0
XJ	XJ	Source/Drain junction depth	150E-9 m
Xdep		depletion depth
AGS	AGS	Coefficient of Vgs dependence of bulk charge effect	0.0 1/V
B0	B0	Bulk charge effect coeff. for channel width	0.0 m
B1	B1	Bulk charge effect width offset	0.0 m
KETA	KETA	Body-bias coefficient of the bulk charge effect	-0.047 1/V

Unified Mobility Model

Mobility of carriers depends on many process parameters and bias conditions. Modeling mobility accurately is critical to precise modeling of MOS transistors. BSIM4 provides three different mobility models, selectable through the MOBMOD flag. The MOBMOD = 0 and 1 models are the same as being used in BSIM3v3. There is a new and accurate universal mobility model, selectable through MOBMOD = 2, which is also suitable for predictive modeling [1].

With BSIM4.5.0, an Leff dependency was added to the formulas for the effective mobility using the newly introduced parameters UD and UP (see parameter list for details).

MOBMOD = 0:

(24)

MOBMOD = 1:

(25)

MOBMOD = 2

(26)

The constant C0 has different values for different MOS processes. For NMOS processes C0 = 2, for PMOS processes C0 = 2.5 is used.

Using UD = 0.0 and UP = 0.0, the model is backwards compatible.

Table 44 Mobility Model Parameters 

Equation Variable	BSIM4 Parameter	Description	Default Value
U0	U0	Low-field mobility	NMOS: 670 PMOS: 250 [cm²/(Vs)]
UA	UA	First-order mobility degradation coefficient due to vertical field	MOBMOD=0, 1: 1E-9 MOBMOD=2: 1e-15 [m/V]
UB	UB	Second-order mobility degradation coefficient	1E-19 (m/V)²
UC	UC	Coefficient of the body-bias effect of mobility degradation	MOBMOD=1: -0.0465 1/V; MOBMOD=0, 2: 0.0465E-9 m/V2
UD	UD	Mobility coulomb scattering coefficient	1E14 (1/m²)
UP	UP	Mobility channel length coefficient	0 (1/m²)
EU	EU	Exponent for mobility degradation of MOBMOD = 2	NMOS: 1.67 PMOS: 1.0

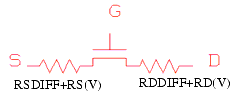
Drain/Source Resistance Model

The resistances of the drain/source regions are modeled using two components: The sheet resistance, which is bias-independent, and a bias-dependent LDD resistance.

In contrast to the BSIM3 models, the drain and source LDD resistances are not necessarily the same, they could be asymmetric. This is a prerequisite for accurate RF simulations.

A further enhancement of the BSIM4 model over BSIM3 is the external or internal RDS option, invoked by the model selector RDSMOD = 0 (internal RDS) or RDSMOD = 1 (external RDS). The external RDS option looks at a resistance connected between the internal and external source and drain nodes. See the following figure.

RDSMOD = 0 (internal Rs(V))

(27)

RDSMOD = 1 (external Rd(V) and Rs(V))

(28)

(29)

The flatband voltage Vfbsd is calculated as follows:

If NGATE > 0:

Else:

Table 45 Drain Source Resistance Parameters

Equation Variable	BSIM4 Parameter	Description	Default Value
NGATE	NGATE	Poly Si-gate doping concentration	0.0 cm-3
PRWB	PRWB	Body bias coefficient of LDD resistance	0.0 V-0.5
PRWG	PRWG	Gate bias dependence of LDD resistance	1.0 1/V
RDSW	RDSW	Zero bias LDD resistance per unit width for RDSMOD = 0	200 (µm)WR
RDSWMIN	RDSWMIN	LDD resistance per unit width at high Vgs and zero Vbs for RDSMOD = 0	0.0 (µm)WR
WR	WR	Channel width dependence parameter of LDD resistance	1.0

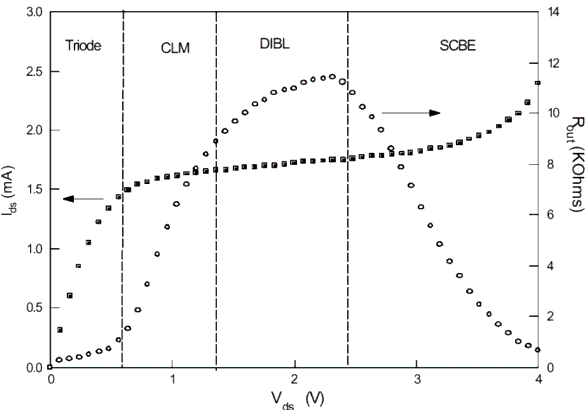
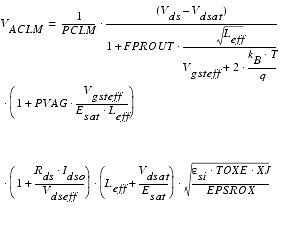
Saturation Region Output Conductance Model

The following figure shows a typical MOSFET Ids vs. Vds diagram. The calculated output resistance is inserted into the diagram as well. This output resistance curve can be divided into four distinct regions, each region is affected by different physical effects. The first region at low Vds is characterized by a very small output resistance. It is called the linear region, where carrier velocity is not yet saturated.

Increasing Vds leads to a region that is dominated by carrier velocity saturation; this is the so-called saturation region. In this region, three different physical mechanisms are controlling device behavior. Those mechanisms are Channel Length Modulation (CLM), Drain-Induced Barrier Lowering (DIBL), and Substrate-Current Induced Body Effect (SCBE). Each of those mechanisms dominate the output resistance in a specific region.

Figure 59 Output Resistance vs. Drain-Source Voltage [1]

The continuous channel current equation for the linear and saturation region as implemented in BSIM4 is:

(30)

The Early voltage VAsat at is used to get continuous expressions for drain current and output resistance between linear and saturation region.

(31)

In this equation, the channel current dependencies are modeled using specific Early voltages VA, as will be described in the following sections.

Channel Length Modulation - CLM

Through integration based on a quasi two-dimensional analysis, we obtain

(32)

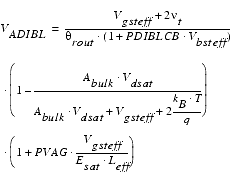
Drain-Induced Barrier Lowering - DIBL

The gate voltage modulates the DIBL effect. To correctly model DIBL, the parameter PDIBLC2 is introduced. This parameter becomes significant only for long channel devices.

(33)

The parameter is channel length dependent in the same manner as the DIBL effect in VTH, but different parameters are used here.

Substrate-Current Induced Body Effect - SCBE

Due to increasing Vds, some electrons flowing from the source of an NMOS device will gain high energies and are able to cause impact ionization. Electron-hole pairs will be generated and the substrate current created by impact ionization will increase exponentially with the drain voltage. The early voltage due to SCBE is calculated by

(34)

If the device is produced using pocket implantation, a potential barrier at the drain end of the channel will be introduced. The potential barrier can be reduced by the drain voltage even in long channel devices. This effect is called Drain-Induced Threshold Shift (DITS) and the early voltage due to DITS is

(35)

Table 46 Saturation Region Output Conductance Parameters

Equation Variable	BSIM4 Parameter	Description	Default Value
DROUT	DROUT	Channel-length dependence coefficient of the DIBL effect on output resistance	0.56
PSCBE1	PSCBE1	First substrate current induced body-effect parameter	4.24E8 V/m
PSCBE2	PSCBE2	Second substrate current induced body-effect coefficient	1.0E-5 m/V
PVAG	PVAG	Gate-bias dependence of Early voltage	0.0
FPROUT	FPROUT	Effect of pocket implant on Rout degradation	0.0 V/m0.5
PDITS	PDITS	Impact of drain-induced Vth shift on Rout	0.0 V-1
PDITSL	PDITSL	Channel-length dependence of drain-induced Vth shift on Rout	0.0
PDITSD	PDITSD	Vds dependence of drain-induced Vth shift on Rout	0.0V-1
PCLM	PCLM	Channel length modulation parameter	1.3
PDIBLC1	PDIBLC1	First output resistance DIBL effect parameter	0.39
PDIBLC2	PDIBLC2	Second output resistance DIBL effect parameter	8.6m
PDIBLCB	PDIBLCB	Body bias coefficient of output resistance DIBL effect	0.0 1/V

Body Current Model

The substrate current of a MOSFET consists of diode junction currents, gate-to-body tunneling current, impact-ionization (Iii) and gate-induced drain leakage currents (IGIDL).

Impact Ionization Model

BSIM4 uses the same impact ionization model as was introduced in BSIM3v3.2. The impact ionization current is calculated by

(36)

Gate-Induced Drain Leakage

The GIDL effect is modeled by

(37)

Table 47 Body Current Model Parameters

Equation Variable	Parameter Name	Description	Default Value
ALPHA0	ALPHA0	First impact ionization parameter	0.0 Am/V
ALPHA1	ALPHA1	Length dependent substrate current parameter	0.0 A/V
BETA0	BETA0	Second impact ionization parameter	30 V
AGIDL	AGIDL	Pre-exponential coefficient for GIDL	0.0 mho (1/Ohm)
BGIDL	BGIDL	Exponential coefficient for GIDL	2.3e9 V/m
CGIDL	CGIDL	Parameter for body-bias effect on GIDL	0.5 V³
EGIDL	EGIDL	Fitting parameter for band bending for GIDL	0.8 V

Stress Effect Modeling

The scaling of CMOS feature sizes makes shallow trench isolation (STI) a popular technology. To enhance device performance, strain channel materials have been used. The mechanical stress introduced by using these processes causes MOSFET performance to become a function of the active device area and the location of the device in the isolated region. Influence of stress on mobility and saturation velocity has been known since the 0.13 um technology [1].

For the named reasons, BSIM4 considers the influence of stress on:

Mobility related dependence of device performance is induced through band structure modification. Doping profile variation results in Vth dependence of the stress effect. Both effects follow the same 1/LOD trend but have different L and W scaling influence. By modifying some parameters in the BSIM model, a phenomenological model has been implemented. The model assumes mobility relative change to be proportional to stress distribution.

Figure 60 MOSFET device geometry using a shallow trench isolation scheme

The figure above shows a typical MOSFET layout surrounded by shallow trench isolation. SA, SB are the distances between trench isolation edge to Gate-PolySi from one and from the other side, respectively. SD is the distance between neighboring fingers of the device. The Length of Oxide Definition (LOD) is expressed through the following equation:

2D simulation shows that stress distribution can be expressed by a simple function of SA and SB.

To cover doping profile changes in devices with different LOD, Vth0, K2, and ETA0 are modified.

The total LOD effect for multiple finger devices is the average of the LOD effect on every finger.

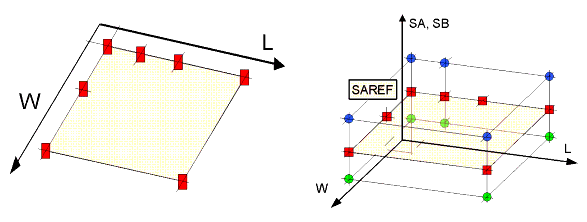
Since MOSFETs often use an irregular shape of their active area, additional instance parameters have to be introduced to fully describe the shape of the active area. This will result in many new parameters in the netlists and an increase in simulation time. To avoid this drawbacks, BSIM4.3.0 uses effective SA and SB values.

Figure 61 A "third" dimension is added to standard geometry parameters of MOSFET devices by introducing new parameters SA and SB to model stress effect influence on device performance

The left part of the figure above shows the geometry parameters used in MOSFET models so far. To the right, the SAREF-plane represents the standard L, W plane which is varied by SA and SB.

Until BSIM4.2.1, gate length (L) and gate width (W) have been the major device geometry parameters required.

For more details regarding the modeled stress effect influences on device performance, see Chapter 13 of the BSIM4.3.0 manual[1].