Regression Analysis

The intent of regression analysis is to provide a quantitative description of the relationship between two or more variables. In the case of simple regression, the objective is to predict the value of a response variable from a single predictor, or regressor. In multiple regression, the value of the response variable is dependent on two or more predictors. For problems involving more than one response variable that is dependent on the same set of predictors, we have what is called multivariate linear regression. Essentially, a multivariate linear regression amounts to nothing more than a collection of multiple regression problems. However, when properly solved, the multivariate problem requires only one matrix inversion operation (as does the single multiple regression operation). Hence, the computational burden of the multivariate problem does not scale in proportion to the number of responses.

For compact semiconductor device modeling problems, the ability to predict model parameters from a smaller set of predictor parameters has some compelling advantages. The smaller set of parameters can be electrical test parameters that are tracked in manufacturing. These predictors can then serve the dual role of providing predictive SPICE models for simulation as well as being used for process tracking. The predictors can also be a subset of the compact model parameters. A regression model can be built using any appropriate predictor(s).

Choosing Predictors

Using factor analysis, it is a fairly straightforward procedure to identify a set of dominant (predictor) device model parameters. These are selected automatically as the parameters that have the highest loading on a given factor. The multivariate regression feature in IC-CAP Statistics takes the dominant parameters from the previously run factor analysis and builds a regression model using these dominant parameters as the regressors. The remaining parameters are taken as the response variables. If for physical reasons, you want to change the dominant parameter for a given factor, choose Analysis > Change Dominant Parameter. By controlling the number of factors in the factor analysis and by changing the default dominant parameters, you have complete control over the predictor (regressor) variables used in the regression.

Solving for the Regression Coefficients

Mathematically, the regression problem requires the solution of the p (number of predictors) by q (number of responses) matrix B of regression coefficients.

Y = XB +

where

Y is the n by q matrix of response parameters values

X is the n by p matrix of predictor parameter values

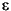is the n by q matrix of errors

n is the number of data samples

the solution B of this equation can be expressed as:

B = [X^TX] ^-1 X^TY

IC-CAP Statistics normalizes the matrix of inputs X prior to evaluating the matrix B, by subtracting the mean and dividing by the standard deviation of the predictor parameters. This results in a better conditioned matrix, since once normalized, entries in the matrix will no longer vary over the many orders of magnitude typically encountered with device model parameters. Upon completion of the solution, the B matrix is un-normalized and is output to the spreadsheet entitled Dominant Parameter Based Equations.

Evaluating the Regression Model

Once the regression coefficients have been computed, the regression model can be used to predict parameter values based on measured or generated values of the predictor variables. The various options for evaluating the regression model can be found by choosing Analysis > Parametric Analysis > Regression Equations. Refer to Parametric Analysis Results Window for more details.

Eigenvalues

An eigenvalue is a scalar associated with a given linear transformation of a vector space and having the property that there is some nonzero vector which when multiplied by the scalar is equal to vector obtained by letting the transformation operate on the vector.

Eigenvalues present a summary of the variances associated with each factor. For example, an eigenvalue of 3.45 indicates that the factor accounts for as much variance in the data collection as would 3.45 variables, on average.