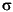Print version of this Book (PDF file)
Factor Analysis
Factor analysis is used to explain relationships among several, difficult to interpret, and correlated variables using a few, conceptually meaningful, and relatively independent factors.
Factor analysis focuses on one or both of the following tasks—an assessment of underlying relationships or dimensions in the data (or what is being measured), and the replacement of original variables with fewer, new variables.
Qualitative Description
Factor analysis is used in IC-CAP Statistics to reduce a set of model parameters to a smaller set of parameters that are statistically independent. This reduced parameter set is called the factors, or in the case of the principal component model, principal components. Henceforth, we will refer to the reduced parameter set as factors, regardless of the particular method used to compute them. These factors can be used to build a mathematical model that predicts parameter values from the independent factors. Alternatively, the independent factors can be used to assist in the identification of a set of dominant parameters. These dominant parameters can then be used as the regressors in a multiple regression model that predicts the remaining model parameters from the dominant (subset) parameters.
Depending on the number of factors that are chosen for a particular model, some percentage of the overall variance in the original parameter set will be accounted for in this factor-space model. For example, given a set of parameter values for an n-parameter model, an n-factor model can be built from the data that will explain all (100%) of the variance in the data. Another way of looking at this is that the correlation matrix of the original parameter set is reproduced exactly by the factor-space model. For an n-parameter problem, a factor model that retains fewer than n factors will explain < 100% of the variance in the original parameter set. In terms of the correlation matrix, this means that the correlations in the original correlation matrix of parameters will not be reproduced exactly by the factor-space model. The distribution of this error within the correlation matrix depends on the particular method used to compute the factors. The three methods available in IC-CAP statistics are: Principal Factor Analysis (PFA), Principal Component Analysis (PCA) and Unweighted Least Squares (ULS). Specifics about each of these methods are discussed later.
Mathematical Description
The primary quantity computed in a factor analysis is the factor loadings matrix, V. The factor loadings matrix is an n by m matrix, where n = number of parameters and m = number of factors, whose individual coefficients represent the correlations between the factors and the parameters. The factor loadings matrix V is related to the predicted correlation matrix Rmod through the following relation:
where VT is the transpose of matrix V. As explained in the previous section, the matrix Rmod, is not equal to the correlation matrix R (computed from the extracted model parameter values), when the number of factors is less than the number if model parameters. Under these conditions, the error in the factor model or the residual correlation is given by
Substituting (1) into (2) and solving for R, we can also write
The key underlying base to common factor analysis is that the chosen model parameters can be transformed into linear combinations of an underlying set of hypothesized or unobserved factors f. The original model parameters are related to the factors through the following relation:
- z is the vector of standardized parameters of length n,
- f is the factor vector of length m,
- e is the error in the model.
- f is the factor vector of length m,
Finally, the standardized parameters are related to the actual parameters x, through the relation
Principal Component Method
Principal component analysis (PCA) is the optimum method for explaining maximum variability in a parameter data set with m factors (principal components). In other words, with m factors, a factor analysis performed with PCA will always return a larger value of total variance explained than either PFA of ULS. From this standpoint, it is the preferred method when building a model to predict parameter values from factors. This is especially true for the case of corner or boundary modeling, where we are attempting to accurately predict the extreme values of a set of correlated parameters.
Recall, that in the previous two sections, the subject of error in the correlation matrix was discussed. Also, recall from the section on Correlation Analysis that the diagonal of the correlation matrix represents the normalized variances of the model parameter data. Since PCA is the optimal method for explaining total variability, it should come as no surprise that the residual correlation matrix, ΔR in PCA, will have its smallest entries along the diagonal. In other words, the PCA model is better at reproducing the variances in the correlation matrix than it is at reproducing interrelationships or the off-diagonal elements in the correlation matrix. You are encouraged to validate this on a set of measured data, by viewing the residual correlation matrix after a PCA is performed and comparing it with the results obtained from either a PFA or ULS analysis.
Principal Factor Analysis and Unweighted Least Squares
In IC-CAP Statistics, the principal component analysis (PCA), principal factor analysis (PFA), and unweighted least squares (ULS) methods have been lumped under the heading of Factor Analysis. This has been done to avoid confusion with disparate terminology, such as factors and components. In addition, from a functional standpoint, the methods accomplish much the same task: They reduce the data to a smaller set of uncorrelated parameters. However, the literature often treats PCA as a separate technique from factor analysis. Indeed, there are significant differences in the techniques used to compute the factor loadings for the principal component and factor models. For applications related to the analysis of device model parameters, however, the only relevant difference between PCA and the "pure" factor methods, PFA and ULS, lies in the way the respective techniques model the correlation matrix.
Recall that the PCA model is optimal for reproducing the diagonals of the correlation matrix. The "pure" factor methods differ from PCA in that they are better at reproducing the off-diagonal elements of the correlation matrix. In other words, the "pure" factor methods explain correlations between parameters or interrelationships better than they explain variability.
In selecting dominant parameters, the desire is to locate parameters that have a high loading on a particular factor. Since PFA and ULS are better at reproducing correlations between factors and parameters, these methods are preferred when your ultimate goal is to generate a set of dominant parameter equations. In this case, the factor analysis is not being used for model construction, but rather, as a means of identifying actual parameters that can be used in place of the factors for model construction (see Regression Analysis). The IC-CAP Statistics module is very flexible and unrestrictive on this point, however. You can construct a model that predicts parameters from factors for any of the three methods: PCA, PFA or ULS. However, as stated previously, the PCA method is preferred for model construction when the factors are the independent variables.
Until now, no distinction has been made between PFA and ULS. All we have said is that they differ from PCA in the way they account for residual errors in the correlation matrix. The ULS (also known as minres or minimum residuals) method is a more recent algorithm than the PFA method. The ULS method operates by minimizing a quantity that is the sum of squared discrepancies between the observed values and the modeled values. Generally speaking, it is thought to be superior to the PFA method for minimizing the off-diagonal elements in the residual correlation matrix. In practice, however, the two methods give very similar results. Computationally, either method is fast enough on a modern computer to allow virtually any device modeling problem to be evaluated with both methods in span of a few seconds. The residual correlation matrices for the two cases can then be compared, and the better performing method can be selected for a given application.
Decisions on Running a Principal Component or Factor Analysis
To analyze data with either principal component analysis or principal factor analysis, three key decisions must be made:
| • | The factor extraction method |
| • | The number of factors to extract |
| • | The transformation method to be used |
Interpretation of a Factor Analysis
There are several areas to be aware of, including:
| • | Magnitude of eigenvalues. Assess the amount of original variance accounted for. Retain factors whose eigenvalues are greater than 1. (Ignore those with eigenvalues less than one as the factor is accounting for less variance than an original variable.) |
| • | Substantive importance. This is an absolute test of eigenvalues in a proportional sense. Retain any eigenvalue that accounts for at least 5% of the variance. |
| • | Interpretability. This is a battery of tests where the above heuristics may all be applied. |
Factor Rotation
The distribution of variance among factors in an unrotated factor analysis follows a definite pattern. The first factor always accounts for the most variance, the second factor accounts for the second largest portion of the variance, and so on. In this model, the factors are independent and orthogonal. Unfortunately, it is difficult to gain an understanding of the underlying meaning of the factors when most of the model parameters load heavily on the first few factors and load very little on the remaining factors.
Factor rotation attempts to redefine the position of the factors such that the loadings tend to be either very high (near 1 or -1) or very low (near 0). This eliminates as many of the medium-sized loadings as possible and aids in the interpretation of the factors. The rotation also results in a more even distribution of variance explained between the factors.
Some examples of applications where the rotation of factors would be helpful include: 1. trying to identify dominant parameters for use in a regression model; 2. attempting to associate a particular processing step with a given factor; and 3. selecting electrical test parameters that could be used as predictors in a regression model. Unfortunately, one of the side effects of rotating the factors is that they are no longer uncorrelated. Consequently, for applications that require building a model using factors as the independent variable, rotation offers little benefit and should be avoided.
Rotation Type
The Rotation Type field in the Factor Analysis dialog box has four choices.
| • | Varimax |
| • | Quartimax |
| • | Equimax |
| • | None (default) |
All three rotation types are orthogonal. Varimax (originated in 1958) is the most popular of these rotation types, with the constant, c, in the orthogonal expression, equal to 1. Quartimax is a slightly older variation, with c = 0. The Equimax variation (1961) treats c = k/2. You should experiment with these rotation types to see which one works best for your work, or choose None.
 )/
)/