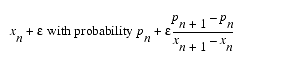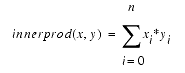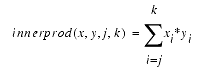Expression Capability

The ADS Simulator has a powerful and flexible symbolic expression capability, called VarEqn, which allows the user to define variables, expressions, and functions in the netlist. These can then be used to define other VarEqn expressions and functions, to specify device parameters and optimization goals, etc.

The names for VarEqn variables, expressions, and functions follow the same hierarchy rules that instance and node names do. Thus, local variables in a subcircuit definition can assume values that differ from one instance of the subcircuit to the next.

Functions and expressions can be defined either globally or locally anywhere in the hierarchy. All variables are local by default. Local variables are known in the subcircuit in which they are defined, and all lower subcircuits; they are not known at higher levels. Expressions defined at the root (the top level) are known everywhere within the circuit. To specify an expression to be global the global keyword must precede the expression. The global keyword causes the variable to be defined at the root of the hierarchy tree regardless of the lexical location.

Examples:

 global exp1 = 2.718

The expression capability includes the standard math operations of + - / * ^ in addition to parenthesis grouping. Scale factors are also allowed in general expressions and have higher precedence than any of the math operators (see Units and Scale Factors).

Constants

An integer constant is represented by a sequence of digits optionally preceded by a negative sign (e.g, 14, -3).

A real number contains a decimal point and/or an exponential suffix using the e notation (e.g, 14.0, -13e-10).

The only complex constant is the predefined constant j which is equal to the square root of -1. It can be used to generate complex constants from real and integer constants (e.g., j*3, 9.1 + j*1.2e-2). The predefined functions complex() and polar() can also be used to enter complex constants into an expression.

A string constant is delimited by single quotes (e.g.,'string','this is a string').

Predefined Constants

Table 71 Predefined Constants

Constant	Definition	Constant	Definition
boltzmann	Boltzmann's constant	ln10	2.30...
c0	Speed of light in a vacuum	j	Square root of -1
DF_DefaultInt	Reference to default int value defined in Data Flow controller	pi	3.14...
DF_ZERO_OHMS	Symbol for use as zero ohms	planck	Planck's constant
e	2.718...	qelectron	Charge of an electron
e0	Permittivity of a vacuum	tinyReal	Smallest real number
hugeReal	Largest real number	u0	Permeability of a vacuum

Variables

General Form:

variableName = constantExpression

Examples:

 x1 = 4.3inches + 3mils
syc_a = cos(1.0+sin(pi*3))
Zin = 7.8k - j*3.2k

The type of a variable is determined by the type of its value. For example, x=1 is an integer, x=1+j is complex, and x = "tuesday" is a string.

Predefined Variables

In addition to the predefined constants, there are several predefined global variables. Since they are variables, they can be modified and swept.

__fdd	Flag to indicate a new FDD instance
__fdd_v	Flag to indicate updated FDD state vars
_ac_state	Is analyses in AC state
_c1 to _c30	Symbolic controlling current
_dc_state	Is analyses in DC state
_freq1 to _freq12	Fundamental frequency
_harm	Harmonic number index for sources and FDD
_hb_state	Is analyses in harmonic balance state
_p2dInputPower	Port input power for P2D simulation
_sigproc_state	Is analyses in signal processing state
_sm_state	Is analyses in sm state
_sp_state	Is analyses in sparameter analysis state
_tr_state	Is analyses in transient state
CostIndex	Index for optimization cost plots
DF_Value	Reference to corresponding value defined in Data Flow controller
DefaultValue	Signal processing default parameter value
DeviceIndex	Device Index used for noise contribution or DC OP output
dcSourceLevel	used for DC source-level sweeping
doeindex	Index for Design of Experiment sweeps
freq	The frequency in Hertz of the present simulation	(1MHz)
logNodesetScale	Used for DC nodeset simulation
logRshunt	Used for DC Rshunt sweeping
mcTrial	Trial counter for Monte Carlo based simulations
noisefreq	The spectral noise analysis frequency
Nsample	Signal processing analysis sample number
optIter	Optimization job iteration counter
temp	The ambient temperature, in degrees Celsius.	(25 degrees)
time	The analysis time
timestep	The analysis time step
tranorder	The transient analysis integration order
ScheduleCycle	Signal processing schedule cycle number
sourcelevel	The relative attenuation of the spectral sources	(1.0)
ssfreq	The small-signal mixer analysis frequency
_v1 to _v19	State variable voltages used by the sdd device
_i1 to _i19	State variable currents used by the sdd device
mc_index	Index variable used by Monte Carlo controller

The sourcelevel variable is used by the spectral analysis when it needs to gradually increase source power from 0 to full scale to obtain convergence. It can be used by the user to sweep the level of ALL spectral source components, but is not recommended. The _v and _i variables should only be used in the context of the sdd device.

Expressions

General Form:

expressionName = nonconstantExpression

Examples:

x1 = 4.3 + freq;
syc_a = cos(1.0+sin(pi*3 + 2.0*x1))
Zin = 7.8 ohm + j*freq * 1.9 ph
y = if (x equals 0) then 1.0e100 else 1/x endif

The main difference between expressions and variables is that a variable can be directly swept and modified by an analysis but an expression cannot. Note however, that any instance parameter that depends on an expression is updated whenever one of the variables that the expression depends upon is changed (e.g., by a sweep).

Predefined Expressions

gaussian =	_gaussian_tol(10.0)	default gaussian distribution
nfmin =	_nfmin()	the minimum noise figure
omega =	2.0*pi*freq	the analysis frequency
rn =	_rn()	the noise resistance
sopt =	_sopt	the optimum noise match
tempkelvin =	temp + 273.15	the analysis temperature
uniform =	_uniform_tol(10.0)	default uniform distribution

Functions

General Form:

functionName( [ arg1, ..., argn ] ) = expression

Examples:

 y_srl(freq, r, l) = 1.0/(r + j*freq*l)
expl(a,b) = exp(a)*step(b-a) + exp(b)*(a-b-1)*step(a-b)

In expression, the function's arguments can be used, as can any other VarEqn variables, expressions, or functions.

Predefined Functions

_discrete_density(...)	user-defined discrete density function
_gaussian( [mean, sigma, lower_n_sigmas, upper_n_sigmas, lower_n_sigmas_del, upper_n_sigmas_del] )	gaussian density function
_gaussian_tol[percent_tol, lower_n_sigmas, upper_n_sigmas, lower_percent_tol, upper_percent_tol, lower_n_sigmas_del, upper_n_sigmas_del] )	gaussian density function (tolerance version)
_get_fnom_freq(...)	Get analysis frequency for FDD carrier frequency index and harmonic
_lfsr(x, y, z)	linear feedback shift register (trigger, seed, taps)
_mvgaussian(...)	multivariate gaussian density function (correlation version)
_mvgaussian_cov(...)	multivariate gaussian density function (covariance version)
_n_state(x, y)	_n_state(arr, val) array index nearest value
_pwl_density(...)	user-defined piecewise-linear density function
_pwl_distribution(...)	user-defined piecewise-linear distribution function
_randvar(distribution, mcindex, [nominal, tol_percent, x_min, x_max, lower_tol, upper_tol, delta_tol, tol_factor] )	random variable function
_shift_reg(x, y, z, t)	(trigger, mode(ParIn:MSB1st), length, input)
_uniform( [lower_bound, upper_bound] )	uniform density function
_uniform_tol([percent_tol, lower_tol, upper_tol] )	uniform density function (tolerance version)
abs(x)	absolute value function
access_all_data(...)	datafile indep+dep lookup/interpolation function
access_data(...)	datafile dependents' lookup/interpolation function
arcsinh(x)	arcsinh function
arctan(x)	arctan function
atan2(y, x)	arctangent function (2 real arguments)
awg_dia(x)	wire gauge to diameter in meters
bin(x)	function convert a binary to integer
bitseq(time, [clockfreq, trise, tfall, vlow, vhigh, bitseq] )	bitsequence function
complex(x, y)	real-to-complex conversion function
conj(x)	complex-conjugate function
cos(x)	cosine function
cos_pulse(time, [low, high, delay, rise, fall, width, period] )	periodic cosine shaped pulse function
cosh(x)	hyperbolic cosine function
cot(x)	cotangent function
coth(x)	hyperbolic cotangent function
ctof(x)	convert Celsius to Fahrenheit
ctok(x)	convert Celsius to Kelvin
cxform(x, y, z)	transform complex data
damped_sin(time, [offset, amplitude, freq, delay, damping, phase] )	damped sin function
db(x)	decibel function
dbm(x, y)	convert voltage and impedance into dbm
dbmtoa(x, y)	convert dbm and impedance into short circuit current
dbmtov(x, y)	convert dbm and impedance into open circuit voltage
dbmtow(x)	convert dBm to Watts
dbpolar(x, y)	(dB,angle)-to-rectangular conversion function
dbwtow(x)	convert dBW to Watts
deembed(x)	deembedding function
deg(x)	radian-to-degree conversion function
dep_data(x, y, [z] )	dependent variable value
dphase(x, y)	Continuous phase difference (radians) between x and y
dsexpr(x, y)	Evaluate a dataset expression to an hpvar
dstoarray(x, [y] )	Convert an hpvar to an array
echo(x)	echo-arguments function
erf_pulse(time, [low, high, delay, rise, fall, width, period] )	periodic error function shaped pulse function
eval_poly(x, y, z)	polynomial evaluation function
exp(x)	exponential function
exp_pulse(time, [low, high, delay1, tau1, delay2, tau2] )	exponential pulse function
fread(x)	raw-file reading function
ftoc(x)	convert Fahrenheit to Celsius
ftok(x)	convert Fahrenheit to Kelvin
get_array_size(x)	Get the size of the array
get_attribute(...)	value of attribute of a set of data
get_block(x, y)	HPvar tree from block name function
get_fund_freq(x)	Get the frequency associated with a specified fundamental index
get_max_points(x, y)	maximum points of independent variable
imag(x)	imaginary-part function
index(x, y, [z, t] )	get index of name in array
innerprod(...)	inner-product function
int(x)	convert-to-integer function
itob(x, [y] )	convert integer to binary
jn(x, y)	bessel function
ktoc(x)	convert Kelvin to Celsius
ktof(x)	convert Kelvin to Fahrenheit
length(x)	returns number of elements in array
limit_warn( [x, y, z, t, u] )	limit, default and warn function
list(...)
ln(x)	natural log function
log(x)	log base 10 function
mag(x)	magnitude function
makearray(...)	(1:real-2:complex-3:string, y, z..) or (array, startIndex, stopIndex)
max(x, y)	maximum function
min(x, y)	minimum function
multi_freq(time, amplitude, freq1, freq2, n, [seed] )	multifrequency function
names(x, y)	array of names of indepVars and/or depVars in dataset
norm(x)	norm function
phase(x)	phase (in degrees) function
phase_noise_pwl(...)	piecewise-linear function for computing phase noise
phasedeg(x)	phase (in degrees) function
phaserad(x)	phase (in radians) function
polar(x, y)	polar-to-rectangular conversion function
polarcpx(...)	polar to rectangular conversion function
pulse(time, [low, high, delay, rise, fall, width, period] )	periodic pulse function
pwl(...)	piecewise-linear function
pwlr(...)	piecewise-linear-repeated function
rad(x)	degree-to-radian conversion function
ramp(x)	ramp function
read_data(...)	read_data("file-dataset", "locName", "fileType")
read_lib(...)	read_lib("libName", "item", "fileType")
real(x)	real-part function
rect(x, y, z)	rectangular pulse function
rem(...)	remainder function
ripple(x, y, z, v)	ripple(amplitude, intercept, period, variable) sinusoidal ripple function
rms(...)	root-mean-square function
rpsmooth(x)	rectangular-to-polar smoothing function
scalearray(x, y)	scalar times a vector (array) function
setDT(x)	Turns on discrete time transient mode (returns argument)
sffm(time, [offset, amplitude, carrier_freq, mod_index, signal_freq] )	signal frequency FM
sgn(x)	signum function
sin(x)	sine function
sinc(x)	sin(x)/x function
sinh(x)	hyperbolic sine function
sprintf(x, y)	formatted print utility
sqrt(x)	square root function
step(x)	step function
tan(x)	tangent function
tanh(x)	hyperbolic tangent function
vswrpolar(x, y)	(VSWR,angle)-to-rectangular conversion function

Detailed Descriptions of the Predefined Functions

_discrete_density (x₁, p₁, x₂, p₂, …) allows the user to define a discrete density distribution: returns x₁ with probability p₁, x₂ with probability p₂, etc. The x_n, p_n pairs needn't be sorted. The p_ns will be normalized automatically.

_gaussian( [mean, sigma, lower_n_sigmas, upper_n_sigmas, lower_n_sigmas_del, upper_n_sigmas_del] ) returns a value randomly distributed according to the standard bell-shaped curve. mean defaults to 0. sigma defaults to 1. lower_n_sigmas, upper_n_sigmas define truncation limits (default to 3). lower_n_sigmas_del and upper_n_sigmas_del define a range in which the probability is zero (a bimodal distribution). _gaussian_tol( [percent_tol, lower_n_sigmas, upper_n_sigmas, lower_percent_tol, upper_percent_tol, lower_n_sigmas_del, upper_n_sigmas_del] ) is similar, but percent_tol defines the percentage tolerance about the nominal value (which comes from the RANDVAR expression).

_get_fnom_freq(x) returns the actual analysis frequency associated with the carrier frequency specified in the surrounding FDD context. If x is negative, it is the carrier frequency index. If x is positive, it is the harmonic index.

_mvgaussian(N, mean₁, … mean_N, sigma₁, … sigma_N, correlation_1,2, …, correlation_1,N, …, correlation_N-1,N) multivariate gaussian density function (correlation version). Returns an N dimensional vector. The correlation coefficient matrix must be positive definite. _mvgaussian_cov(N, mean₁, … mean_N, sigma₁, … sigma_N, covariance_1,2, ..., covariance_1,N, ..., covariance_N-1,N) is similar, but defined in terms of covariance. The covariance matrix must be positive definite.

_pwl_density(x₁, p₁, x₂, p₂, …) returns a value randomly distributed according to the piecewise-linear density function with values p_n at x_n, i.e. it will return x_n with probability p_n and return

The x_n, p_n pairs needn't be sorted. The p_ns will be normalized automatically. _pwl_distribution(x₁, p₁, x₂, p₂, …) is similar, but is defined in terms of the distribution values. It will return a value less than or equal to x_n with probability p_n. The x_n, p_n pairs will be sorted in increasing x_n order. After sorting, the p_ns should never decrease. The p_ns will be normalized so that p_N=1.

_randvar(distribution, mcindex, [nominal, tol_percent, x_min, x_max, lower_tol, upper_tol, delta_tol, tol_factor] ) returns a value randomly distributed according to the distribution. The value will be the same for a given value of mcindex. The other parameters are interpreted according to the distribution.

_shift_reg(x, y, z, t) implements a z-bit shift register. x specifies the trigger. y = 0 means LSB First, Serial To Parallel, 1 means MSB First, Serial To Parallel, 2 means LSB First, Parallel to Serial, 3 means MSB First, Parallel to Serial. t is the input (output) value.

_uniform( [lower_bound, upper_bound] ) returns a value between lower_bound and upper_bound. All such values are equally probable. _uniform_tol( [percent_tol, lower_tol, upper_tol] ) is similar, but tolerance version.

access_all_data(InterpMode, source, indep₁, dep₁ …) datafile independent and dependent lookup/interpolation function.

access_data(InterpMode, nData, source, dep₁ …) datafile dependents' lookup/interpolation function.

bin(String) calculates the integer value of a sequence of 1's and 0's. For example bin('11001100') = 204. The argument of the bin function must be a string denoted by single quotes. The main use of the bin function is with the System Model Library to define an integer which corresponds to a digital word.

cxform(x, OutFormat, InFormat) transform complex data x from format InFormat to format OutFormat. The values for OutFormat and InFormat are 0: real and imaginary, 1: magnitude (linear) and phase (degrees), 2: magnitude (linear) and phase (radians), 3: magnitude (dB) and phase (degrees), 4: magnitude (dB) and phase (radians), 5: magnitude (SWR) and phase (degrees), 6: magnitude (SWR) and phase (radians). For example, to convert linear magnitude and phase in degrees to real and imaginary parts:

 result = cxform(invar, 0, 1)

damped_sin(time, [offset, amplitude, freq, delay, damping, phase]). See Transient Source Functions.

The function db(x) is a shorthand form for the expression: 20log(mag(x)).

The deembed(x) function takes an array, x, of 4 complex numbers (the 2-port S-parameter array returned from the VarEqn interp() function) and returns an array of equivalent de-embedding S-parameters for that network. The array must be of length 4 (2 x 2--two-port data only), or an error message will result. The transformation used is:

where det is the determinant of the 2 x 2 array.

The function deg(x) converts from radians to degrees.

dphase(x, y) Calculates phase difference phase(x)-phase(y) (in radians).

dsexpr(x, y) Evaluate x, a DDS expression, to an hpvar. y is the default location data directory.

echo(x) prints argument on terminal and returns it as a value.

erf_pulse(time, [low, high, delay, rise, fall, width, period] ) periodic pulse function, edges are error function (integral of Gaussian) shaped.

eval_poly(x, y, z) y is a real number. z is an integer that describes what to evaluate: -1 means the integral of the polynomial, 0 means the polynomial itself, +1 means the derivative of the polynomial. x is a VarEqn array that contains real numbers. The polynomial is

exp_pulse(time, [low, high, delay1, tau1, delay2, tau2]) See Transient Source Functions.

get_fund_freq(fund) returns the value of frequency (in Hertz) of a given fundamental defined by fund.

index(nameArray, "varName", [caseSense, length] ) returns position of "varName" in nameArray, -1 if not found. caseSense sets case-sensitivity, defaults to yes. length sets how many characters to check, defaults to 0 (all).

innerprod(x, y) forms the inner product of the vectors x and y:

j and k are optional integers which specify a range of harmonics to include in the calculation:

j defaults to 0 and k defaults to infinity.

int(x) Truncates the fractional part of x.

itob(x, [bits] ) convert integer x to bits-bit binary string.

The function jn(n, x) is the n-th order bessel function evaluated at x.

limit_warn( [Value, Min, Max, default, Name] ) sets Value to default, if not set. Limits it to Min and Max and generates a warning if the value is limited.

makearray(arg1[,arg2,..] creates an array with elements defined by arg1 to argN where N can be any number of arguments. The data type of args must be Integer, Real, or Complex and the same for all args.

 word = bin('1101')
fibo = makearray(0,1,1,2,3,5,8,word)
foo = fibo[0]

multi_freq(time, amplitude, freq1, freq2, n, [seed] ) seed defaults to 1. If it is 0, phase is set to 0, otherwise it is used as a seed for a randomly-generated phase.

norm(x) returns the L-2 norm of the spectrum x:

j and k are optional integers which specify a range of harmonics to include in the calculation:

j defaults to 0 and k defaults to infinity.

phase(x) is the same as phasedeg(x).

The function phasedeg(x) returns phase in degrees.

The function phaserad(x) returns phase in radians.

The function polarcpx(x[,leave_as_real]) takes a complex argument, assumes that the real and complex part of the argument represents mag and phase (in radians) information, and converts it to real/imaginary. If the argument is real or integer instead of complex, the imaginary part is assumed to be zero. However, if the optional leave_as_real variable is specified, and is the value ``1'' (note that the legal values are ``0'' and ``1'' only), a real argument will be not be converted to a complex one.

pulse(time, [low, high, delay, rise, fall, width, period]) See Transient Source Functions.

pwl(...) piecewise-linear function. See Transient Source Functions.

pwlr(...) piecewise-linear-repeated function.

The function rect(t, tc, tp) is pulse function of variable t centered at time tc with duration tp.

The function rad(x) converts from degrees to radians.

ramp(x) 0 for , x for

read_data(source, locName, [fileType]) returns data from a file or dataset. source = "file" --- "dataset". locName is the name of the source. fileType specifies the file type.

read_lib(libName, locName, [fileType]) returns data from a library. libName is the name of the library. locName is the name of the source. fileType specifies the file type. read_lib("libName", "item", "fileType")

rect(x, y, z) Returns:

z	|x - y| < |z|	|x - y| > |z|
> 0	1	0
< 0	0	1

rem(x, [y]) Returns remainder of dividing x/y. y defaults to 0 (which returns x).

rms(x) returns the RMS value (including DC) of the spectrum x:

j and k are optional integers which specify a range of harmonics to include in the calculation:

j defaults to 0 and k defaults to infinity.

The function rpsmooth(x) takes a VarEqn pointer (one returned by readraw()), converts to polar format the rectangular data given by the VarEqn pointer, and smooths out `phase discontinuities'.

sffm(time, [offset, amplitude, carrier_freq, mod_index, signal_freq]) See Transient Source Functions.

The sprintf() function is similar to the C function which takes a format string for argument s and a print argument x (x must be a string, an integer, or a real number) and returns a formatted string. This string then may be written to the console using the system function with an echo command.

Transient Source Functions

There are several built-in functions that mimic Spice transient sources. They are:

SPICE source	ADS Simulator function
exponential	exp_pulse(time, low, high, tdelay1, tau1, tdelay2, tau2)
single-frequency FM	sffm(time, offset, amplitude, carrier_freq, mod_index, signal_freq)
damped sine	damped_sin(time, offset, amplitude, freq, delay, damping)
pulse	pulse(time, low, high, delay, rise, fall, width, period)
piecewise linear	pwl(time, t1, x1, ..., tn, xn)

There functions are typically used with the vt parameter of the voltage source and the it parameter of the current source.

exp_pulse

Examples:

 ivs:vin n1 0 vt=exp_pulse(time)
ics:iin n1 0 it=exp_pulse(time, -0.5mA, 0.5mA, 10ns, 5ns,
20ns, 8ns)

Arguments for exp_pulse
Name	Optional	Default
TIME	NO
LOW	YES	0
HIGH	YES	1
TDELAY1	YES	0
TAU1	YES	TSTEP
TDELAY2	YES	TDELAY1 + TSTEP
TAU2	YES	TSTEP

TSTEP is the output step-time time specified on the TRAN analysis.

sffm

Examples:

 ivs:vin n1 0 vt=sffm(time, , , , 0.5)
ics:iin n1 0 it=sffm(time, 0, 2, 1GHz, 1.2, 99MHz)

Arguments for sffm
Name	Optional	Default
TIME	NO
OFFSET	YES	0
AMPLITUDE	YES	1
CARRIER_FREQ	YES	1/TSTOP
MOD_INDEX	YES	0
SIGNAL_FREQ	YES	1/TSTOP

TSTOP is the stop time specified on the TRAN analysis.

damped_sin

Examples:

 ivs:vin n1 0 vt=damped_sin(time)
ics:iin n1 0 it=damped_sin(time, 0, 5V, 500MHz, 50ns, 200ns)

Arguments for damped_sin
Name	Optional	Default
TIME	NO
OFFSET	YES	0
AMPLITUDE	YES	1
FREQ	YES	1/TSTOP
DELAY	YES	0
DAMPING	YES	1/TSTOP

TSTOP is the stop time specified on the TRAN analysis.

pulse

Examples:

 ivs:vin n1 0 vt=pulse(time)
ics:iin n1 0 it=pulse(time, -5V, 5V, 500MHz, 50ns, 200ns)

Arguments for pulse
Name	Optional	Default
TIME	NO
LOW	YES	0
HIGH	YES	1
DELAY	YES	0
RISE	YES	TSTEP
FALL	YES	TSTEP
WIDTH	YES	TSTOP
PERIOD	YES	TSTOP

TSTEP is the output step-time time specified on the TRAN analysis. TSTOP is the stop time specified on the TRAN analysis.

pwl

Examples:

 ivs:vin n1 0 vt=pulse(time, 0, 0, 1ns, 1, 10ns, 1, 15ns, 0)
ics:iin n1 0 it=pwl(time, 0, 0, 1ns, 1, 5ns, 1, 5ns, 0.5,
10ns,0.5, 15ns, 0)

Arguments for pwl
Name	Optional	Default
TIME	NO
T1	NO
X1	NO
T2	YES	NONE
X2	YES	NONE
. . .	. . .	. . .
TN	YES	NONE
XN	YES	NONE

Conditional Expressions

The ADS Simulator supports simple in-line conditional expressions:

 if boolExpr then expr else expr endif
if boolExpr then expr elseif boolExpr then expr else expr
endif

boolExpr is a boolean expression, that is, an expression that evaluates to TRUE or FALSE.

expr is any non-boolean expression.

The else is required (because the conditional expression must always evaluate to some value).

There can be any number of occurrences of elseif expr then expr.

A conditional expression can legally occur as the right-hand side of an expression or function definition or, if parenthesized, anywhere in an expression that a variable can occur.

Boolean operators

equals	logical equals
=	logical equals
==	logical equals
notequals	logical not equals
!=	logical not equals
not	logical negative
!	logical negative
and	logical and
&&	logical and
or	logical or
||	logical or
<	less than
>	greater than
<=	less than or equals
>=	greater than or equals

Boolean expressions

A boolean expression must evaluate to TRUE or FALSE and, therefore, must contain a relational operator (equals, =, ==, notequals, !=, <, >, <=, or >=).

The only legal place for a boolean expression is directly after an if or an elseif.

A boolean expression cannot stand alone, that is,

 x = a > b

is illegal.

Precedence

Tightest binding: equals, =, ==, notequals, !=, >, <, >=, <=

NOT, !

AND,

Loosest binding: OR, ||

All arithmetic operators have tighter binding than the boolean operators.

Evaluation

Boolean expressions are short-circuit evaluated. For example, if when evaluating a and b, expression a evaluates to FALSE, expression b will not be evaluated.

During evaluation of boolean expressions with arithmetic operands, the operand with the lower type is promoted to the type of the other operand. For example, in 3 equals x +j*b, 3 is promoted to complex.

A complex number cannot be used with <, >, <=, or >=. Nor can an array (and remember that strings are arrays). This will cause an evaluation-time error.

Pointers can be compared only with pointers.

Examples:

Protect against divide by zero:

 f(a) = if a equals 0 then 1.0e100 else 1.0/a endif

Nested if's #1:

 f(mode) = if mode equals 0 then 1-a else f2(mode) endif
f2(mode) = if mode equals 1 then log(1-a) else f3(mode) endif
f3(mode) = if mode equals 2 then exp(1-a) else 0.0 endif

Nested if's #2:

 f(mode) = if mode equals 0 then 1-a elseif mode equals 1 then \
log(1-a) elseif mode equals 2 then exp(1-a) else 0.0 endif

Soft exponential:

 exp_max = 1.0e16
x_max = ln(exp_max)
 exp_soft(x) = if x<x_max then exp(x) else 
                                   (x+1-x_max)*exp_max endif