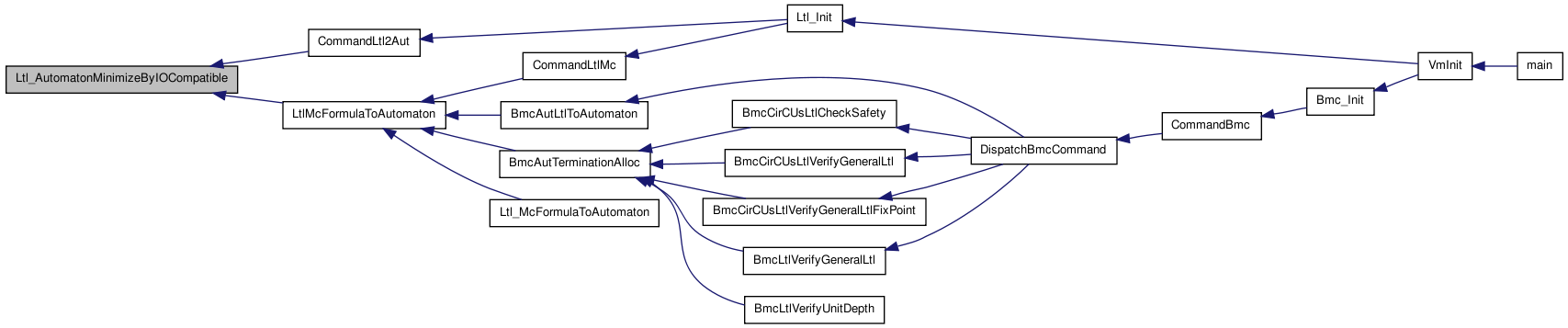
#include "ltlInt.h"
Include dependency graph for ltlMinimize.c:
Go to the source code of this file.
Functions | |
| static lsList | AutomatonPickInputCandidate (graph_t *G, vertex_t *vtx) |
| static lsList | AutomatonPickOutputCandidate (graph_t *G, vertex_t *vtx) |
| static st_table * | AutomatonVertexGetPreImg (graph_t *G, vertex_t *vtx) |
| static st_table * | AutomatonVertexGetImg (graph_t *G, vertex_t *vtx) |
| static int | AutomatonVertexHasSelfLoop (graph_t *G, vertex_t *vtx) |
| static int | AutomatonPfairEquivQfair (Ltl_Automaton_t *A, vertex_t *state, vertex_t *otherstate) |
| static int | AutomatonPfairImplyQfair (Ltl_Automaton_t *A, vertex_t *state, vertex_t *otherstate) |
| static char * | StTableDelete (st_table *tbl, char *item) |
| static st_table * | StTableAppend (st_table *tbl1, st_table *tbl2) |
| static st_table * | StTableRestrict (st_table *tbl1, st_table *tbl2) |
| static st_table * | StTableSubtract (st_table *tbl1, st_table *tbl2) |
| static int | StTableIsEqual (st_table *tbl1, st_table *tbl2, st_table *dontcare) |
| static int | StTableInclude (st_table *large, st_table *small, st_table *dontcare) |
| static int | StTableIsDisjoint (st_table *tbl1, st_table *tbl2, st_table *dontcare) |
| static int | StTableIsFair (lsList A_Fair, st_table *Class) |
| static int | AutomatonPartitionIsClique (graph_t *G, st_table *set) |
| static st_table * | AutomatonPartitionLabelLUB (st_table *set, array_t *Negate) |
| static st_table * | AutomatonPartitionLabelGLB (st_table *set, array_t *Negate) |
| static st_table * | AutomatonQuotientVertexGetClass (vertex_t *vtx) |
| int | Ltl_AutomatonMinimizeByIOCompatible (Ltl_Automaton_t *A, int verbosity) |
| int | Ltl_AutomatonMinimizeByDirectSimulation (Ltl_Automaton_t *A, int verbosity) |
| void | Ltl_AutomatonAddFairStates (Ltl_Automaton_t *A) |
| int | Ltl_AutomatonMaximizeByDirectSimulation (Ltl_Automaton_t *A, int verbosity) |
| int | Ltl_AutomatonMinimizeByReverseSimulation (Ltl_Automaton_t *A, int verbosity) |
| int | Ltl_AutomatonMinimizeByPrune (Ltl_Automaton_t *A, int verbosity) |
| void | Ltl_AutomatonComputeSCC (Ltl_Automaton_t *A, int force) |
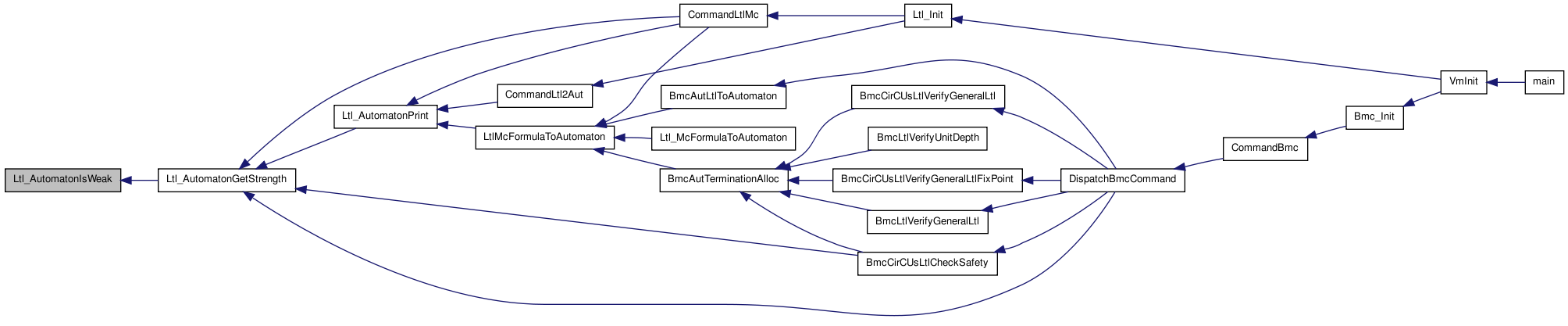
| int | Ltl_AutomatonIsWeak (Ltl_Automaton_t *A) |
| Mc_AutStrength_t | Ltl_AutomatonGetStrength (Ltl_Automaton_t *A) |
| Ltl_Automaton_t * | Ltl_AutomatonCreateQuotient (Ltl_Automaton_t *A, st_table *partition) |
| int | Ltl_AutomatonVtxGetNodeIdx (vertex_t *v) |
| LtlSet_t * | LtlAutomatonVertexGetLabels (vertex_t *vtx) |
Variables | |
| static char rcsid[] | UNUSED = "$Id: ltlMinimize.c,v 1.33 2009/04/09 02:21:13 fabio Exp $" |
Function Documentation
| static int AutomatonPartitionIsClique | ( | graph_t * | G, |
| st_table * | set | ||
| ) | [static] |
Function********************************************************************
Synopsis [Return 1 if the given table forms a clique (for each state, there are edges to all the states in the set).]
SideEffects []
Definition at line 2228 of file ltlMinimize.c.
{
int flag = 1;
st_table *Img;
st_generator *stgen;
vertex_t *state;
st_foreach_item(set, stgen, &state, NIL(char *)) {
Img = AutomatonVertexGetImg(G, state);
flag = StTableInclude(Img, set, NIL(st_table));
st_free_table(Img);
if (!flag) {
st_free_gen(stgen);
break;
}
}
return flag;
}
Here is the call graph for this function:
Here is the caller graph for this function:
| static st_table * AutomatonPartitionLabelGLB | ( | st_table * | set, |
| array_t * | Negate | ||
| ) | [static] |
Function********************************************************************
Synopsis [Find the Greatest Lower Bound of the labels of a set of states, and Return a hash table of A state that satisfy this 'GLB'. Return null if the hash table is empty.]
SideEffects [The result should be freed by the caller.]
Definition at line 2309 of file ltlMinimize.c.
{
vertex_t *state, *least;
LtlSet_t *glb, *label;
st_table *tbl;
st_generator *stgen;
least = NIL(vertex_t);
glb = NIL(LtlSet_t);
st_foreach_item(set, stgen, &state, NIL(char *)) {
label = LtlAutomatonVertexGetLabels(state);
if (!glb)
glb = LtlSetCopy(label);
else
LtlSetOR(glb, glb, label);
if (LtlSetIsContradictory(glb, Negate)) {
least = NIL(vertex_t);
st_free_gen(stgen);
break;
}else if (!least) {
if (LtlSetEqual(glb, label))
least = state;
}else if (!LtlSetEqual(glb, LtlAutomatonVertexGetLabels(least))) {
if (LtlSetEqual(glb, label))
least = state;
else
least = NIL(vertex_t);
}
}
if (glb)
LtlSetFree(glb);
if (least) {
tbl = st_init_table(st_ptrcmp, st_ptrhash);
st_insert(tbl, least, least);
}else
tbl = NIL(st_table);
return tbl;
}
Here is the call graph for this function:
Here is the caller graph for this function:
| static st_table * AutomatonPartitionLabelLUB | ( | st_table * | set, |
| array_t * | Negate | ||
| ) | [static] |
Function********************************************************************
Synopsis [Find the Least Upper Bound of the labels of a set of states, and Return a hash table of states that satisfy this 'LUB'. Return null if the hash table is empty.]
SideEffects [The result should be freed by the caller.]
Definition at line 2260 of file ltlMinimize.c.
{
vertex_t *state;
st_table *greatest = NIL(st_table);
st_generator *stgen;
LtlSet_t *lub = NIL(LtlSet_t);
LtlSet_t *label;
st_foreach_item(set, stgen, &state, NIL(char *)) {
label = LtlAutomatonVertexGetLabels(state);
if (greatest) {
if (LtlSetEqual(label, lub))
st_insert(greatest, state, state);
else if (LtlSetInclude(lub, label)) {
LtlSetAssign(lub, label);
st_free_table(greatest);
greatest = st_init_table(st_ptrcmp, st_ptrhash);
st_insert(greatest, state, state);
}else if (!LtlSetInclude(label, lub)) {
st_free_table(greatest);
greatest = NIL(st_table);
st_free_gen(stgen);
break;
}
}else {
lub = LtlSetCopy(label);
greatest = st_init_table(st_ptrcmp, st_ptrhash);
st_insert(greatest, state, state);
}
}
if (lub)
LtlSetFree(lub);
return greatest;
}
Here is the call graph for this function:
Here is the caller graph for this function:
| static int AutomatonPfairEquivQfair | ( | Ltl_Automaton_t * | A, |
| vertex_t * | state, | ||
| vertex_t * | otherstate | ||
| ) | [static] |
Function********************************************************************
Synopsis [Return 1 iff the following statement in the automaton holds: For each fair set, both states are in it or none of them]
SideEffects []
Definition at line 1925 of file ltlMinimize.c.
{
int flag = 1;
st_table *FairSet;
lsGen lsgen;
lsForEachItem (A->Fair, lsgen, FairSet) {
if (st_is_member(FairSet, state) !=
st_is_member(FairSet, otherstate)) {
flag = 0;
lsFinish(lsgen);
break;
}
}
return flag;
}
Here is the caller graph for this function:
| static int AutomatonPfairImplyQfair | ( | Ltl_Automaton_t * | A, |
| vertex_t * | state, | ||
| vertex_t * | otherstate | ||
| ) | [static] |
Function********************************************************************
Synopsis [Return 1 iff the following statement in the automaton holds: For each fair set, if 'state' is in it, 'otherstate' must also in it.]
SideEffects []
Definition at line 1955 of file ltlMinimize.c.
{
int flag = 1;
st_table *FairSet;
lsGen lsgen;
lsForEachItem (A->Fair, lsgen, FairSet) {
if (st_is_member(FairSet, state) &&
!st_is_member(FairSet, otherstate)) {
flag = 0;
lsFinish(lsgen);
break;
}
}
return flag;
}
Here is the caller graph for this function:
| static lsList AutomatonPickInputCandidate | ( | graph_t * | G, |
| vertex_t * | vtx | ||
| ) | [static] |
AutomaticStart
Function********************************************************************
Synopsis [Return the input-compatible candidates.]
SideEffects [Result should be freed by the caller.]
Definition at line 1725 of file ltlMinimize.c.
{
st_table *uTable;
lsList candi, preImg;
lsGen lsgen, lsgen2;
edge_t *e, *e2;
vertex_t *s, *t;
int size;
preImg = g_get_in_edges(vtx); /* shouldn't be freed */
size = lsLength(preImg);
/* No predecessor */
if (size == 0) {
return lsCopy(g_get_vertices(G), (lsGeneric (*)(lsGeneric)) NULL);
}
/* The only predecessor is itself */
if (size == 1) {
lsFirstItem(preImg, &e, NIL(lsHandle));
if (g_e_source(e) == vtx) { /* all the vertices in G */
return lsCopy(g_get_vertices(G), (lsGeneric (*)(lsGeneric)) NULL);
}
}
/* Has predecessor(s) other than itself */
uTable = st_init_table(st_ptrcmp, st_ptrhash);
candi = lsCreate();
lsForEachItem (preImg, lsgen, e) {
s = g_e_source(e);
foreach_out_edge(s, lsgen2, e2) {
t = g_e_dest(e2);
if (t != vtx) {
if(!st_insert(uTable, t, t))
lsNewEnd(candi, (lsGeneric) t, NIL(lsHandle));
}
}
if (size == 1) {
if (!st_insert(uTable, s, s))
lsNewEnd(candi, (lsGeneric)s, NIL(lsHandle));
}
}
st_free_table(uTable);
return candi;
}
Here is the caller graph for this function:
| static lsList AutomatonPickOutputCandidate | ( | graph_t * | G, |
| vertex_t * | vtx | ||
| ) | [static] |
Function********************************************************************
Synopsis [Return the output-compatible candidates.]
SideEffects [Result should be freed by the caller.]
Definition at line 1780 of file ltlMinimize.c.
{
st_table *uTable;
lsList candi, Img;
lsGen lsgen, lsgen2;
edge_t *e, *e2;
vertex_t *s, *t;
int size;
Img = g_get_out_edges(vtx);
size = lsLength(Img);
/* No successor */
if (size == 0) {
return lsCopy(g_get_vertices(G), (lsGeneric (*)(lsGeneric)) NULL);
}
/* The only successor is itself */
if (size == 1) {
lsFirstItem(Img, &e, NIL(lsHandle));
if (g_e_dest(e) == vtx) {
return lsCopy(g_get_vertices(G), (lsGeneric (*)(lsGeneric)) NULL);
}
}
/* Has successor(s) other than itself */
uTable = st_init_table(st_ptrcmp, st_ptrhash);
candi = lsCreate();
lsForEachItem(Img, lsgen, e) {
s = g_e_dest(e);
foreach_in_edge(s, lsgen2, e2) {
t = g_e_source(e2);
if (t != vtx) {
if(!st_insert(uTable, t, t))
lsNewEnd(candi, (lsGeneric) t, NIL(lsHandle));
}
}
if (size == 1) {
if(!st_insert(uTable, s, s))
lsNewEnd(candi, (lsGeneric)s, NIL(lsHandle));
}
}
st_free_table(uTable);
return candi;
}
Here is the caller graph for this function:
| static st_table * AutomatonQuotientVertexGetClass | ( | vertex_t * | vtx | ) | [static] |
Function********************************************************************
Synopsis [Return the partition component (a st_table) associated with the given vertex in the Quotient graph.]
SideEffects [The result is owned by the node, and should NOT be freed.]
Definition at line 2363 of file ltlMinimize.c.
{
Ltl_AutomatonNode_t *node = (Ltl_AutomatonNode_t *)vtx->user_data;
return node->Class;
}
Here is the caller graph for this function:
| static st_table * AutomatonVertexGetImg | ( | graph_t * | G, |
| vertex_t * | vtx | ||
| ) | [static] |
Function********************************************************************
Synopsis [Return the image of the given vertex in the hash table.]
SideEffects [Result should be freed by the caller.]
Definition at line 1865 of file ltlMinimize.c.
{
lsList Img;
lsGen lsgen;
edge_t *e;
vertex_t *s;
st_table *uTable;
Img = g_get_out_edges(vtx);
uTable = st_init_table(st_ptrcmp, st_ptrhash);
lsForEachItem(Img, lsgen, e) {
s = g_e_dest(e);
st_insert(uTable, s, s);
}
return uTable;
}
Here is the caller graph for this function:
| static st_table * AutomatonVertexGetPreImg | ( | graph_t * | G, |
| vertex_t * | vtx | ||
| ) | [static] |
Function********************************************************************
Synopsis [Return the pre-image of the given vertex in the hash table.]
SideEffects [Result should be freed by the caller.]
Definition at line 1836 of file ltlMinimize.c.
{
lsList preImg;
lsGen lsgen;
edge_t *e;
vertex_t *s;
st_table *uTable;
preImg = g_get_in_edges(vtx);
uTable = st_init_table(st_ptrcmp, st_ptrhash);
lsForEachItem(preImg, lsgen, e) {
s = g_e_source(e);
st_insert(uTable, s, s);
}
return uTable;
}
Here is the caller graph for this function:
| static int AutomatonVertexHasSelfLoop | ( | graph_t * | G, |
| vertex_t * | vtx | ||
| ) | [static] |
Function********************************************************************
Synopsis [Return 1 iff the given vertex has a self-loop.]
SideEffects []
Definition at line 1894 of file ltlMinimize.c.
{
lsList Img;
lsGen lsgen;
edge_t *e;
int flag = 0;
Img = g_get_out_edges(vtx);
lsForEachItem(Img, lsgen, e) {
if (g_e_dest(e) == vtx) {
flag = 1;
lsFinish(lsgen);
break;
}
}
return flag;
}
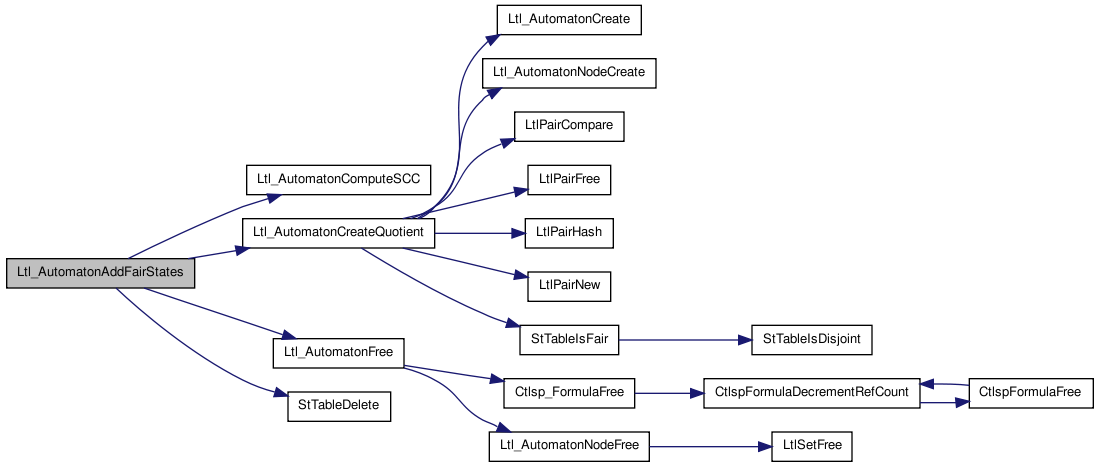
Here is the caller graph for this function:
| void Ltl_AutomatonAddFairStates | ( | Ltl_Automaton_t * | A | ) |
Function********************************************************************
Synopsis [Mark trivial SCCs as Fair states]
Description [Mark trivial SCCs as Fair states]
SideEffects []
SeeAlso []
Definition at line 620 of file ltlMinimize.c.
{
long isFair;
lsGen lsgen1;
st_generator *stgen, *stgen2;
st_table *FairSet, *Class;
Ltl_AutomatonComputeSCC(A, 1);
if (A->Q) {
Ltl_AutomatonFree((gGeneric) A->Q);
A->Q = NIL(Ltl_Automaton_t);
}
A->Q = Ltl_AutomatonCreateQuotient(A, A->SCC);
/*
Mark trivial SCCs as Fair states
*/
st_foreach_item(A->SCC, stgen, &Class, &isFair) {
vertex_t *state;
if (isFair == 2) { /* trivial SCC */
lsForEachItem (A->Fair, lsgen1, FairSet) {
st_foreach_item(Class, stgen2, &state, NIL(char *)) {
if (!st_is_member(FairSet, state)) {
if (st_is_member(A->dontcare, state)){
StTableDelete(A->dontcare, (char *)state);
}
st_insert(FairSet, state, state);
}
}
}
}
}
}
Here is the call graph for this function:
| void Ltl_AutomatonComputeSCC | ( | Ltl_Automaton_t * | A, |
| int | force | ||
| ) |
Function********************************************************************
Synopsis [Compute the SCCs of the Automaton.]
Description [Traverse the entire reachable graph of the automaton, and put all the SCCs in a hash table.
If force=1, the existing partition (A->SCC) is freed and the new partition is computed. If force=0, the partition is computed only if A->SCC=null.]
SideEffects [A->SCC is assigned the new partition.]
SeeAlso []
Definition at line 1357 of file ltlMinimize.c.
{
st_generator *stgen;
st_table *component;
/* compute A->SCC if not exist */
if (!force && A->SCC)
return;
if (force && A->SCC) {
st_foreach_item(A->SCC, stgen, &component, NIL(char *)) {
st_free_table(component);
}
st_free_table(A->SCC);
}
A->SCC = g_SCC(A->G, A->Init);
return;
}
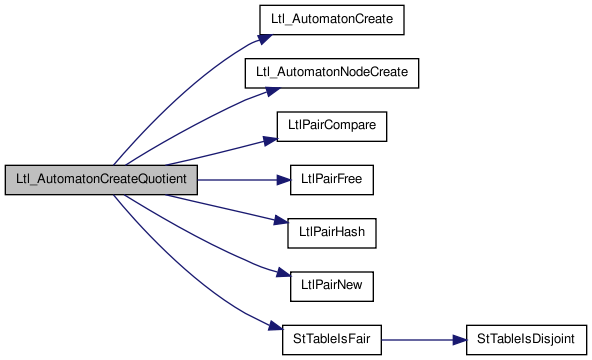
Here is the caller graph for this function:
| Ltl_Automaton_t* Ltl_AutomatonCreateQuotient | ( | Ltl_Automaton_t * | A, |
| st_table * | partition | ||
| ) |
Function********************************************************************
Synopsis [Return the Quotient graph for the given partition.]
Description [The Quotient graph is represented as an automaton Q:
Q->SCC : partition component TO vertex in Q graph hash table Q->Init: initial vertices in Q graph Q->Fair: only 1 FairSet in it, which contains the Q vertices corresponding to the fair components Q->G : The actual graph_t
Each Q vertex is associated with an automaton node: node->index: the index # of the Q vertex node->Class: the partition component associated with this vertex.
NOTICE: the Quotient graph is NOT a DAG, non-trivial SCCs have self-loops.]
SideEffects [A->SCC is updated with the following information: if (key) is a trivial SCC (obviously non-fair), (value)=2; if (key) is a non-trivial non-fair SCC, (value) = 0; if (key) is a fair SCC, (value)=1; otherwise, (value)=1; The result should be freed by the caller.]
SeeAlso []
Definition at line 1579 of file ltlMinimize.c.
{
long isFair;
int flag;
st_generator *stgen, *stgen1;
st_table *Class, *FairSet;
lsGen lsgen;
st_table *Avtx2Qvtx, *Class2Qvtx, *EdgeUtable;
Ltl_Automaton_t *Q;
Ltl_AutomatonNode_t *node;
vertex_t *q, *p;
edge_t *e;
LtlPair_t *pair;
/* create the Q graph as a Automaton */
Q = Ltl_AutomatonCreate();
Q->isQuotientGraph = 1;
/*### for each class, add vtx in Q->G ###*/
/* hash tables : (vtx in A, vtx in Q), (class_st_table, vtx in Q) */
Avtx2Qvtx = st_init_table(st_ptrcmp, st_ptrhash);
Class2Qvtx = st_init_table(st_ptrcmp, st_ptrhash);
st_foreach_item(partition, stgen, &Class, NIL(char *)) {
/* add 'q' in Q->G */
q = g_add_vertex(Q->G);
node = Ltl_AutomatonNodeCreate(Q);
node->Class = Class;
q->user_data = (gGeneric) node;
st_insert(Class2Qvtx, Class, q);
/* hash table (A_vtx -> Q_vtx) */
flag = 0;
st_foreach_item(Class, stgen1, &p, NIL(char *)) {
st_insert(Avtx2Qvtx, p, q);
if (st_is_member(A->Init, p))
flag = 1;
}
/* if any state in class is in A->Init, put class into Q->Init */
if (flag)
st_insert(Q->Init, q, q);
}
/*### for each (class, class2), add edges ###*/
/* edge unique table in Q graph, key = (class, class2) */
EdgeUtable = st_init_table(LtlPairCompare, LtlPairHash);
pair = LtlPairNew(0,0);
foreach_edge(A->G, lsgen, e) {
if (!st_lookup(Avtx2Qvtx, g_e_source(e), &pair->First))
continue;
if (!st_lookup(Avtx2Qvtx, g_e_dest(e), &pair->Second))
continue;
/* only consider reachable states in A->G */
if (!st_is_member(EdgeUtable, pair)) {
LtlPair_t *tmpPair = LtlPairNew(pair->First, pair->Second);
st_insert(EdgeUtable, tmpPair, tmpPair);
g_add_edge((vertex_t *)pair->First, (vertex_t *)pair->Second);
}
}
/*### put fair sccs into the only FairSet ###*/
/* isFair = 1 (fair SCC); isFair = 0 (non-trivial non-fair SCC);
* isFair = 2 (dontcare: trivial SCC, obviously non-fair)*/
FairSet = st_init_table(st_ptrcmp, st_ptrhash);
st_foreach_item(partition, stgen, &Class, &isFair) {
st_insert(partition, Class, (char *)0);
/* it should be a nontrivial scc (size >1 or have self-loop) */
if (st_count(Class)==1) {
st_lookup(Class2Qvtx, Class, &pair->First);
st_lookup(Class2Qvtx, Class, &pair->Second);
if (!st_is_member(EdgeUtable, pair)) {
/*trivial scc (1 state without self-loop) */
st_insert(partition, Class, (char *)2);
continue;
}
}
/* for non trivial SCC, check if it intersect all FairSets */
if (!StTableIsFair(A->Fair, Class)) continue;
/* it's a "fair SCC" */
st_insert(partition, Class, (char *)1);
st_lookup(Class2Qvtx, Class, &pair->First);
st_insert(FairSet, pair->First, pair->First);
}
lsNewEnd(Q->Fair, (lsGeneric) FairSet, (lsHandle *) 0);
/* free */
LtlPairFree(pair);
st_foreach_item(EdgeUtable, stgen, &pair, NIL(char *)) {
LtlPairFree(pair);
}
st_free_table(EdgeUtable);
st_free_table(Avtx2Qvtx);
/* st_free_table(Class2Qvtx); */
Q->SCC = Class2Qvtx;
return Q;
}
Here is the call graph for this function:
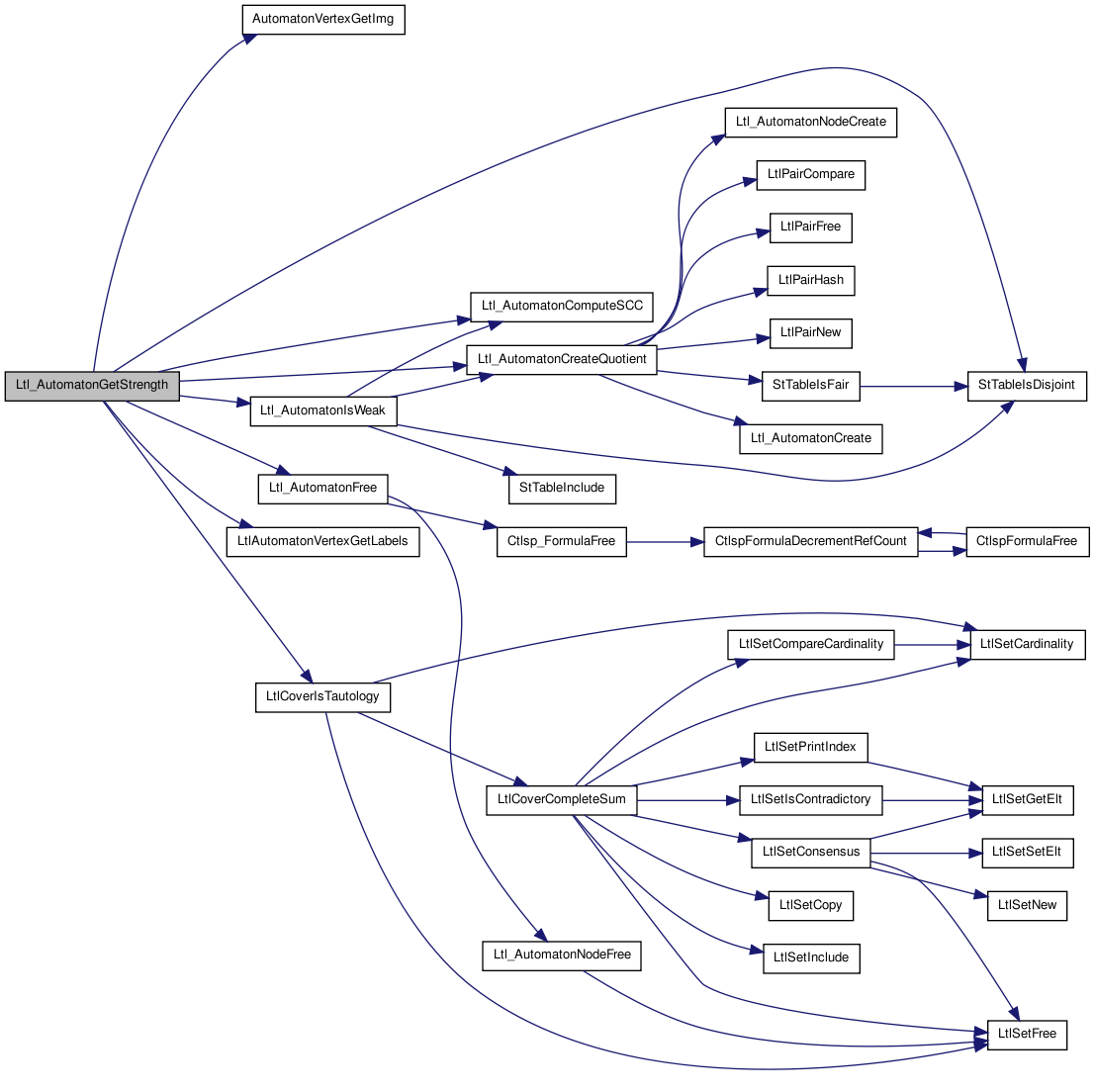
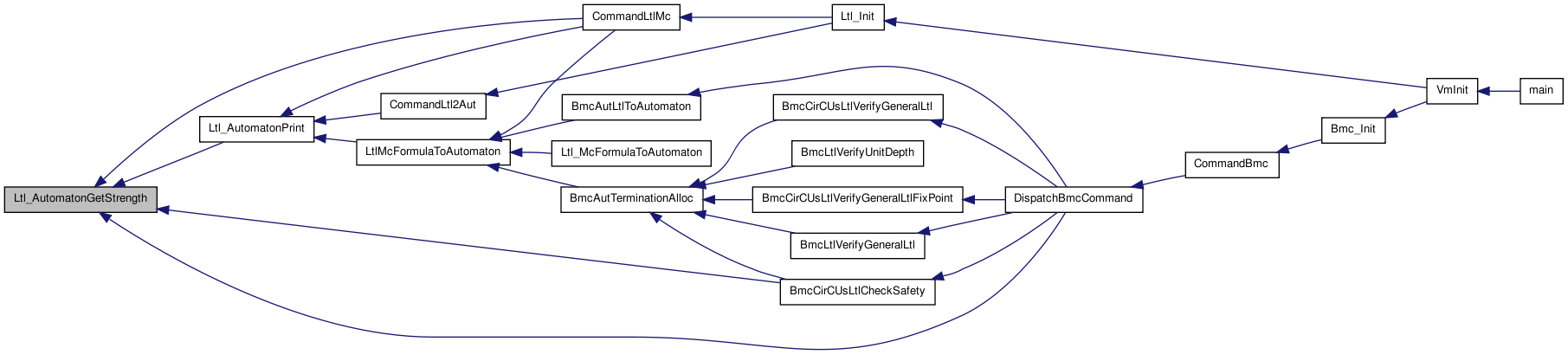
Here is the caller graph for this function:
| Mc_AutStrength_t Ltl_AutomatonGetStrength | ( | Ltl_Automaton_t * | A | ) |
Function********************************************************************
Synopsis [Return the strength of the automaton.]
Description [0 -terminal 1 -weak 2 -strong.]
SideEffects [Compute the parition and quotient graph if not exist.]
SeeAlso []
Definition at line 1461 of file ltlMinimize.c.
{
Mc_AutStrength_t result;
vertex_t *qstate, *state, *state2;
st_generator *stgen, *stgen1, *stgen2;
st_table *tbl, *FairSet, *scc;
lsList cover;
lsGen lsgen;
/* Every time we need to re-compute the partition(A->SCC) and
* the Quotient graph(A->Q)
*/
Ltl_AutomatonComputeSCC(A, 1);
if (A->Q) {
Ltl_AutomatonFree((gGeneric) A->Q);
A->Q = NIL(Ltl_Automaton_t);
}
A->Q = Ltl_AutomatonCreateQuotient(A, A->SCC);
/* is it strong ? */
if (!Ltl_AutomatonIsWeak(A))
return Mc_Aut_Strong_c /*2*/;
/* it's terminal (0) if all the weak SCCs are COMPLETE and FINAL.*/
result = Mc_Aut_Terminal_c;
st_foreach_item(A->SCC, stgen, &scc, NIL(char *)) {
int disjoint_flag = 1;
int final_flag = 1;
int complete_flag = 1;
/* if it does not intersect any fair set, we don't care about it */
if (lsLength(A->Fair) == 0)
disjoint_flag = 0;
else {
lsForEachItem(A->Fair, lsgen, FairSet) {
if (!StTableIsDisjoint(FairSet, scc, NIL(st_table))) {
disjoint_flag = 0;
lsFinish(lsgen);
break;
}
}
}
if (disjoint_flag) continue;
/* FINAL:
* it shouldn't be trivial, and shouldn't have edge to other sccs
*/
st_lookup(A->Q->SCC, scc, &qstate);
tbl = AutomatonVertexGetImg(A->Q->G, qstate);
final_flag = (st_count(tbl) == 1 && st_is_member(tbl, qstate));
st_free_table(tbl);
if (!final_flag) {
st_free_gen(stgen);
result = Mc_Aut_Weak_c; /* weak */
break;
}
/* COMPLETE:
* for each state in the SCC: the union of the labels in all
* its successors is tautology
*/
st_foreach_item(scc, stgen1, &state, NIL(char *)) {
tbl = AutomatonVertexGetImg(A->G, state);
cover = lsCreate();
st_foreach_item(tbl, stgen2, &state2, NIL(char *)) {
lsNewEnd(cover, (lsGeneric)LtlAutomatonVertexGetLabels(state2),
NIL(lsHandle));
}
st_free_table(tbl);
complete_flag = LtlCoverIsTautology(cover, A->labelTableNegate);
lsDestroy(cover, (void (*)(lsGeneric))0);
if (!complete_flag) {
st_free_gen(stgen1);
break;
}
}
if (!complete_flag) {
st_free_gen(stgen);
result = Mc_Aut_Weak_c; /* weak */
break;
}
}
/* Weak = 1; Terminal = 0 */
return result;
}
Here is the call graph for this function:
Here is the caller graph for this function:
| int Ltl_AutomatonIsWeak | ( | Ltl_Automaton_t * | A | ) |
Function********************************************************************
Synopsis [Return 1 if if the automaton is 'WEAK']
Description [The definition of WEAK: For each fair SCC in the automaton, every fairset F contains all its states.
A special case: If there is no fairness constraint at all, it's WEAK.]
SideEffects [Compute the SCCs and Quotient graph(A->SCC,A->Q) if not exist.]
SeeAlso []
Definition at line 1395 of file ltlMinimize.c.
{
int weak;
long isFair;
st_generator *stgen;
st_table *scc, *FairSet;
lsGen lsgen;
/* A SCC without fairness constraint is WEAK */
if (lsLength(A->Fair) == 0)
return 1;
/* compute the partition(A->SCC) and Quotient graph(A->Q) if not exist */
if (!A->SCC)
Ltl_AutomatonComputeSCC(A,0);
if (!A->Q)
A->Q = Ltl_AutomatonCreateQuotient(A, A->SCC);
/* weak: for each SCC,
* either it's included in all FairSets
* or it intersects none of them
*/
weak = 1;
st_foreach_item(A->SCC, stgen, &scc, &isFair) {
int flag = 0;
/* intersect none of them ? */
lsForEachItem (A->Fair, lsgen, FairSet) {
if (!StTableIsDisjoint(FairSet, scc, NIL(st_table))) {
lsFinish(lsgen);
flag = 1;
break;
}
}
if (!flag) continue;
/* included in all of them ? */
lsForEachItem (A->Fair, lsgen, FairSet) {
if (!StTableInclude(FairSet, scc, NIL(st_table))) {
weak = 0;
lsFinish(lsgen);
break;
}
}
if (!weak) {
st_free_gen(stgen);
break;
}
}
return weak;
}
Here is the call graph for this function:
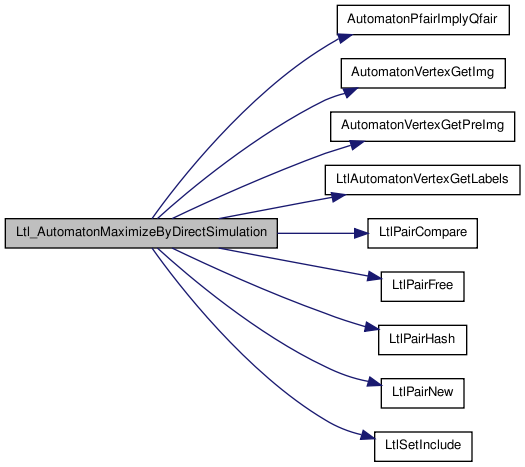
Here is the caller graph for this function:
| int Ltl_AutomatonMaximizeByDirectSimulation | ( | Ltl_Automaton_t * | A, |
| int | verbosity | ||
| ) |
Function********************************************************************
Synopsis [Maximize the Automaton using Direct Simulation.]
Description [Compute direct-simulation relation, and minimize the automaton according to the following two cases: 1) Remove p if (p,q) is a Bi-simulation relation (Bis-aa) 2) Remove edges from their common predecessors to p if p is direct simulated by q.]
SideEffects [The automaton might be changed. if so, return 1.]
SeeAlso []
Definition at line 675 of file ltlMinimize.c.
{
int changed = 0;
int flag = 0;
lsList states, otherstates, queue;
lsGen lsgen, lsgen1;
vertex_t *state, *otherstate;
vertex_t *p, *q, *s, *t, *u, *v;
LtlSet_t *set, *set2;
st_table *tbl0, *tbl1, *tbl2, *tbl3;
st_table *simul, *enqueued;
st_generator *stgen, *stgen1, *stgen2;
LtlPair_t *pair, *pair2;
/*
Ltl_AutomatonAddFairStates(A);
*/
/* store the simulation-relation in hash tables and queue list */
simul = st_init_table(LtlPairCompare, LtlPairHash);
enqueued = st_init_table(LtlPairCompare, LtlPairHash);
queue = lsCreate();
/*######################################
* Initialize sim rln to all pairs (p,q)
*######################################
*/
states = lsCopy(g_get_vertices(A->G), (lsGeneric (*)(lsGeneric)) NULL);
otherstates = lsCopy(states, (lsGeneric (*)(lsGeneric)) NULL);
lsForEachItem (states, lsgen, state) {
lsForEachItem (otherstates, lsgen1, otherstate) {
/* p != q */
if (state == otherstate) continue;
/* L(p) \leq L(q) (set(Lp) > set(Lq) */
set = LtlAutomatonVertexGetLabels(state);
set2 = LtlAutomatonVertexGetLabels(otherstate);
if (!LtlSetInclude(set, set2)) continue;
/* p \in F -> q \in F */
if (!AutomatonPfairImplyQfair(A, state, otherstate)) continue;
/* put (state, otherstate) into simul-relation (candidate) */
pair = LtlPairNew((char *)state, (char *)otherstate);
st_insert(simul, pair, pair);
st_insert(enqueued, pair, pair);
lsNewEnd(queue, (lsGeneric)pair, NIL(lsHandle));
}
}
lsDestroy(states, (void (*)(lsGeneric)) NULL);
lsDestroy(otherstates, (void (*)(lsGeneric)) NULL);
/*######################################
* Compute the "Greatest Fixpoint"
*######################################
*/
while (lsDelBegin(queue, &pair) != LS_NOMORE) {
st_delete(enqueued, &pair, NIL(char *));
p = (vertex_t *)pair->First;
q = (vertex_t *)pair->Second;
/* Check for each 's' in Img(p), if there exists a 't' in Img(q) such
* that (s, t) is in simulation relation candidate list
*/
tbl0 = AutomatonVertexGetImg(A->G, p);
tbl1 = AutomatonVertexGetImg(A->G, q);
st_foreach_item(tbl0, stgen, &s, NIL(char *)) {
flag = 0;
st_foreach_item(tbl1, stgen1, &t, NIL(char *)) {
flag = (s==t);
if (flag) {
st_free_gen(stgen1);
break;
}
pair2 = LtlPairNew((char *)s, (char *)t);
flag = st_is_member(simul, pair2);
LtlPairFree(pair2);
if (flag) {
st_free_gen(stgen1);
break;
}
}
if (!flag) {
st_free_gen(stgen);
break;
}
}
st_free_table(tbl0);
st_free_table(tbl1);
if (flag) continue;
/* (p, q) is not a simulation relation */
st_delete(simul, &pair, &pair);
LtlPairFree(pair);
/* Enqueue perturbed pairs */
tbl2 = AutomatonVertexGetPreImg(A->G, p);
tbl3 = AutomatonVertexGetPreImg(A->G, q);
st_foreach_item(tbl2, stgen1, &u, NIL(char *)) {
st_foreach_item(tbl3, stgen2, &v, NIL(char *)) {
pair2 = LtlPairNew((char *)u, (char *)v);
if (st_lookup(simul, pair2, &pair)) {
if (!st_is_member(enqueued, pair2)) {
st_insert(enqueued, pair, pair);
lsNewEnd(queue, (lsGeneric)pair, NIL(lsHandle));
}
}
LtlPairFree(pair2);
}
}
st_free_table(tbl2);
st_free_table(tbl3);
}
lsDestroy(queue, (void (*)(lsGeneric))0);
st_free_table(enqueued);
/*######################################
* Add arcs to direct-simulated states
*######################################
*/
/* so that we can modify simul with the for-loop */
tbl0 = st_copy(simul);
st_foreach_item (tbl0, stgen, &pair, NIL(char *)) {
/* 'p' is simulated by 'q' */
p = (vertex_t *)pair->First;
q = (vertex_t *)pair->Second;
/*
Add arcs from the predecessors of q to p
*/
tbl2 = AutomatonVertexGetPreImg(A->G, p);
tbl3 = AutomatonVertexGetPreImg(A->G, q);
st_foreach_item(tbl3, stgen1, &s, NIL(char *)) {
if (!st_is_member(tbl2, s)){
g_add_edge(s, p);
changed = 1;
}
}
st_free_table(tbl2);
st_free_table(tbl3);
}
st_free_table (tbl0);
st_foreach_item(simul, stgen, &pair, NIL(char *)) {
LtlPairFree(pair);
}
st_free_table (simul);
return changed;
}
Here is the call graph for this function:
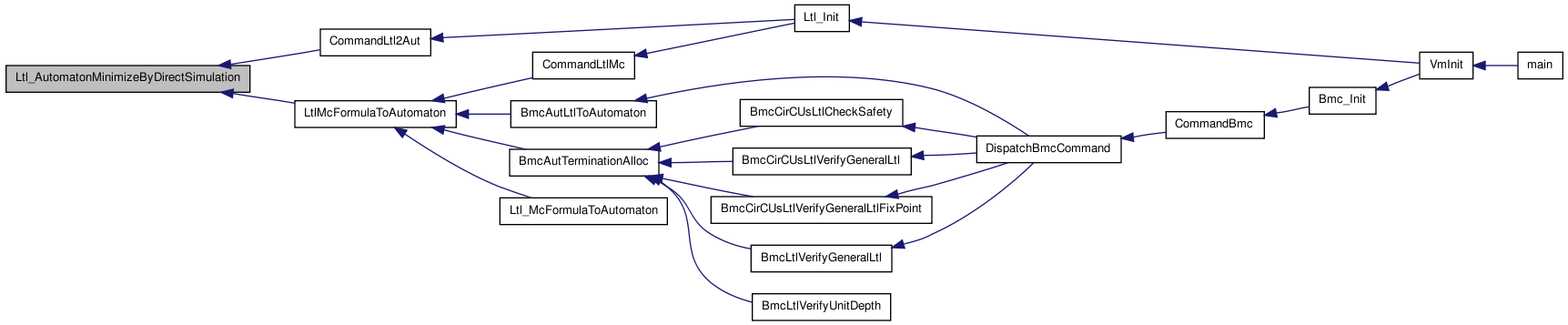
Here is the caller graph for this function:
| int Ltl_AutomatonMinimizeByDirectSimulation | ( | Ltl_Automaton_t * | A, |
| int | verbosity | ||
| ) |
Function********************************************************************
Synopsis [Minimize the Automaton using Direct Simulation.]
Description [Compute direct-simulation relation, and minimize the automaton according to the following two cases: 1) Remove p if (p,q) is a Bi-simulation relation (Bis-aa) 2) Remove edges from their common predecessors to p if p is direct simulated by q.]
SideEffects [The automaton might be changed. if so, return 1.]
SeeAlso []
Definition at line 385 of file ltlMinimize.c.
{
int changed = 0;
int flag = 0;
lsList states, otherstates, list, queue;
lsGen lsgen, lsgen1;
edge_t *e;
vertex_t *state, *otherstate;
vertex_t *p, *q, *s, *t, *u, *v;
LtlSet_t *set, *set2;
st_table *FairSet, *tbl0, *tbl1, *tbl2, *tbl3;
st_table *simul, *enqueued;
st_generator *stgen, *stgen1, *stgen2;
LtlPair_t *pair, *pair2;
/* store the simulation-relation in hash tables and queue list */
simul = st_init_table(LtlPairCompare, LtlPairHash);
enqueued = st_init_table(LtlPairCompare, LtlPairHash);
queue = lsCreate();
/*######################################
* Initialize sim rln to all pairs (p,q)
*######################################
*/
states = lsCopy(g_get_vertices(A->G), (lsGeneric (*)(lsGeneric)) NULL);
otherstates = lsCopy(states, (lsGeneric (*)(lsGeneric)) NULL);
lsForEachItem (states, lsgen, state) {
lsForEachItem (otherstates, lsgen1, otherstate) {
/* p != q */
if (state == otherstate) continue;
/* L(p) \leq L(q) (set(Lp) > set(Lq) */
set = LtlAutomatonVertexGetLabels(state);
set2 = LtlAutomatonVertexGetLabels(otherstate);
if (!LtlSetInclude(set, set2)) continue;
/* p \in F -> q \in F */
if (!AutomatonPfairImplyQfair(A, state, otherstate)) continue;
/* put (state, otherstate) into simul-relation (candidate) */
pair = LtlPairNew((char *)state, (char *)otherstate);
st_insert(simul, pair, pair);
st_insert(enqueued, pair, pair);
lsNewEnd(queue, (lsGeneric)pair, NIL(lsHandle));
}
}
lsDestroy(states, (void (*)(lsGeneric)) NULL);
lsDestroy(otherstates, (void (*)(lsGeneric)) NULL);
/*######################################
* Compute the "Greatest Fixpoint"
*######################################
*/
while (lsDelBegin(queue, &pair) != LS_NOMORE) {
st_delete(enqueued, &pair, NIL(char *));
p = (vertex_t *)pair->First;
q = (vertex_t *)pair->Second;
/* Check for each 's' in Img(p), if there exists a 't' in Img(q) such
* that (s, t) is in simulation relation candidate list
*/
tbl0 = AutomatonVertexGetImg(A->G, p);
tbl1 = AutomatonVertexGetImg(A->G, q);
st_foreach_item(tbl0, stgen, &s, NIL(char *)) {
flag = 0;
st_foreach_item(tbl1, stgen1, &t, NIL(char *)) {
flag = (s==t);
if (flag) {
st_free_gen(stgen1);
break;
}
pair2 = LtlPairNew((char *)s, (char *)t);
flag = st_is_member(simul, pair2);
LtlPairFree(pair2);
if (flag) {
st_free_gen(stgen1);
break;
}
}
if (!flag) {
st_free_gen(stgen);
break;
}
}
st_free_table(tbl0);
st_free_table(tbl1);
if (flag) continue;
/* (p, q) is not a simulation relation */
st_delete(simul, &pair, &pair);
LtlPairFree(pair);
/* Enqueue perturbed pairs */
tbl2 = AutomatonVertexGetPreImg(A->G, p);
tbl3 = AutomatonVertexGetPreImg(A->G, q);
st_foreach_item(tbl2, stgen1, &u, NIL(char *)) {
st_foreach_item(tbl3, stgen2, &v, NIL(char *)) {
pair2 = LtlPairNew((char *)u, (char *)v);
if (st_lookup(simul, pair2, &pair)) {
if (!st_is_member(enqueued, pair2)) {
st_insert(enqueued, pair, pair);
lsNewEnd(queue, (lsGeneric)pair, NIL(lsHandle));
}
}
LtlPairFree(pair2);
}
}
st_free_table(tbl2);
st_free_table(tbl3);
}
lsDestroy(queue, (void (*)(lsGeneric))0);
st_free_table(enqueued);
/*######################################
* Simplify by Bi-Sim equivalent states
*######################################
*/
/* to store removed states */
tbl1 = st_init_table(st_ptrcmp, st_ptrhash);
/* so that we can modify 'simul' within for loop */
tbl0 = st_copy(simul);
st_foreach_item (tbl0, stgen, &pair, NIL(char *)) {
p = (vertex_t *)pair->First;
q = (vertex_t *)pair->Second;
/* make sure neither has been removed */
if (st_is_member(tbl1, p) || st_is_member(tbl1, q))
continue;
/* make sure it is Bi-simulation by testing the other direction */
pair2 = LtlPairNew((char *)q, (char *)p);
flag = st_lookup(simul, pair2, &pair);
LtlPairFree(pair2);
if (!flag) continue;
/*#### Direct BI-SIMULATION equivalent states####*/
/* Theorem applies */
/* remove its swap: (q, p) from simul-rln */
st_delete(simul, &pair, &pair);
LtlPairFree(pair);
/* Remove p, and connect its predecessors to q */
tbl2 = AutomatonVertexGetPreImg(A->G, p);
tbl3 = AutomatonVertexGetPreImg(A->G, q);
st_foreach_item(tbl2, stgen1, &s, NIL(char *)) {
if (s == p) continue;
if (!st_is_member(tbl3, (char *)s))
g_add_edge(s, q);
}
st_free_table(tbl2);
st_free_table(tbl3);
/* Update the fair sets */
lsForEachItem (A->Fair, lsgen, FairSet) {
StTableDelete(FairSet, (char *)p);
}
/* If 'p' is in Q0, Remove 'p' and put 'q' in Q0 */
if (st_is_member(A->Init, p)) {
st_delete(A->Init, &p, NIL(char *));
if (!st_is_member(A->Init, q))
st_insert(A->Init, q, q);
}
/* Remove 'p' from dontcare (if it's in it ) */
StTableDelete(A->dontcare, (char *)p);
/* Remove 'p' from the automaton */
st_insert(tbl1, p, p);
g_delete_vertex(p, Ltl_AutomatonNodeFree, (void(*)(gGeneric))0);
changed = 1;
}
st_free_table(tbl0);
/*######################################
* Remove arcs to direct-simulated states
*######################################
*/
/* so that we can modify simul with the for loop */
tbl0 = st_copy(simul);
st_foreach_item (tbl0, stgen, &pair, NIL(char *)) {
/* 'p' is simulated by 'q' */
p = (vertex_t *)pair->First;
q = (vertex_t *)pair->Second;
/* Make sure neither hasn't been removed yet */
if (st_is_member(tbl1, p) || st_is_member(tbl1, q))
continue;
/*#### p is direct-simulated by q####*/
/* Theorem applies */
/* Drop arcs from their common predecessors to p */
tbl3 = AutomatonVertexGetPreImg(A->G, q);
list = lsCopy(g_get_in_edges(p), (lsGeneric (*)(lsGeneric)) NULL);
lsForEachItem (list, lsgen, e) {
if (!st_is_member(tbl3, g_e_source(e))) continue;
g_delete_edge(e, (void (*)(gGeneric))0);
changed = 1;
}
lsDestroy(list, (void (*)(lsGeneric)) 0);
st_free_table(tbl3);
/* Remove 'p' from Q0 if 'q' is in Q0 */
if (st_is_member(A->Init, q)) {
StTableDelete(A->Init, (char *)p);
changed = 1;
}
}
st_free_table (tbl0);
st_free_table (tbl1);
st_foreach_item(simul, stgen, &pair, NIL(char *)) {
LtlPairFree(pair);
}
st_free_table (simul);
return changed;
}
Here is the call graph for this function:
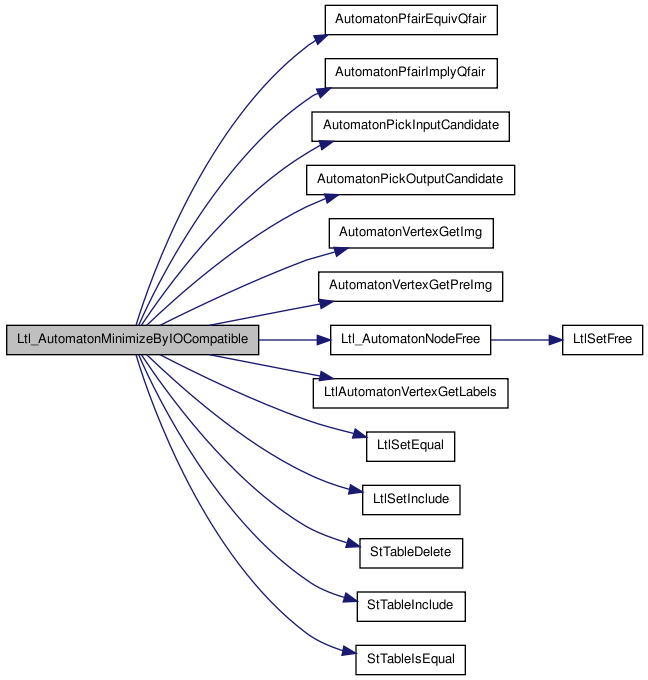
Here is the caller graph for this function:
| int Ltl_AutomatonMinimizeByIOCompatible | ( | Ltl_Automaton_t * | A, |
| int | verbosity | ||
| ) |
AutomaticEnd Function********************************************************************
Synopsis [Minimize the Automaton using I/O Compatiblility and Dominance.]
Description [These minimizations are based on the structural information, and are less effective than simulation-based techniques. They are used for pre-processing since they are faster.Also, in some cases they go beyond what simulation based minimization can do.
Here we consider 3 cases: Input Compatible, Output Compatible and Dominance.]
SideEffects [The automaton might be changed. In that case return 1.]
SeeAlso []
Definition at line 93 of file ltlMinimize.c.
{
int changed = 0;
int flag;
lsList states, incand, outcand;
lsGen lsgen, lsgen2, lsgen3;
vertex_t *state, *otherstate, *s;
LtlSet_t *set, *set2;
st_table *FairSet, *tbl0, *tbl1, *tbl2, *tbl3, *tbl4;
st_generator *stgen;
/* We go through all the states in A->G, and check for Input-Compatible,
* Output-Compatible, and Dominance
*/
states = lsCopy(g_get_vertices(A->G), (lsGeneric (*)(lsGeneric)) NULL);
lsForEachItem (states, lsgen, state) {
int localchanged = 0;
/* Compute the Image adn PreImg of 'state' for later use */
tbl0 = AutomatonVertexGetPreImg(A->G, state);
tbl1 = AutomatonVertexGetImg(A->G, state);
/* ############################
* Check for Input Compatible
* ############################*/
incand = AutomatonPickInputCandidate(A->G, state);
lsForEachItem (incand, lsgen2, otherstate) {
/* p is 'state', q is 'otherstate' */
/* p != q */
if (state == otherstate) continue;
/* L(p) = L(q) */
set = LtlAutomatonVertexGetLabels(state);
set2 = LtlAutomatonVertexGetLabels(otherstate);
if (!LtlSetEqual(set, set2)) continue;
/* p \in Q0 <-> q \in Q0 */
if (st_is_member(A->Init, state) !=
st_is_member(A->Init, otherstate))
continue;
/* p \in F <-> q \in F */
if (!AutomatonPfairEquivQfair(A, state, otherstate)) continue;
/* preImg(p) - {p,q} == preImg(q) - {p,q} */
tbl2 = AutomatonVertexGetPreImg(A->G, otherstate);
tbl3 = st_init_table(st_ptrcmp, st_ptrhash);
st_insert(tbl3, state, state);
st_insert(tbl3 , otherstate, otherstate);
flag = StTableIsEqual(tbl0, tbl2, tbl3);
st_free_table(tbl2);
st_free_table(tbl3);
if (!flag) continue;
/* q \in [delta(p)+delta(q)] <-> p \in [delta(p)+delta(q)] */
tbl2 = AutomatonVertexGetImg(A->G, otherstate);
if ( (st_is_member(tbl1,state) ||
st_is_member(tbl2,state))
!=
(st_is_member(tbl1,otherstate) ||
st_is_member(tbl2,otherstate)) ) {
st_free_table(tbl2);
continue;
}
/* ######## (state, otherstate) :: input compatible #######
* we merge the two state by deleting 'state'
* Notice that now we have the following data available:
* tbl0 = PreImg(state),
* tbl1 = Img(state),
* tbl2 = Img(otherstate)
*/
/* Update intial states */
StTableDelete(A->Init, (char *)state);
/* Add edges (otherstate, s), here s is the sucessor of 'state' */
st_foreach_item(tbl1, stgen, &s, NIL(char *)) {
if (s != state && !st_is_member(tbl2, s))
g_add_edge(otherstate, s);
}
/* Remove 'otherstate' also if state isn't in dontcare */
if (!st_is_member(A->dontcare, state))
StTableDelete(A->dontcare, (char *)otherstate);
/* Remove 'state' from dontcare (if applicable) */
StTableDelete(A->dontcare, (char *)state);
/* Update fairness conditions */
lsForEachItem (A->Fair, lsgen3, FairSet) {
StTableDelete(FairSet, (char *)state);
}
/* Remove 'state' from the automaton */
g_delete_vertex(state, Ltl_AutomatonNodeFree, (void(*)(gGeneric))0);
st_free_table(tbl2);
/* terminate iteration on incand list */
changed = localchanged = 1;
lsFinish(lsgen2);
break;
}
lsDestroy(incand, (void (*)(lsGeneric)) 0);
if (localchanged) {
st_free_table(tbl0);
st_free_table(tbl1);
continue;
}
/* ############################
* Check for Output Compatible
* ############################
*/
outcand = AutomatonPickOutputCandidate(A->G, state);
lsForEachItem (outcand, lsgen2, otherstate) {
/* p != q */
if (state == otherstate) continue;
/* L(p) = L(q) */
set = LtlAutomatonVertexGetLabels(state);
set2 = LtlAutomatonVertexGetLabels(otherstate);
if (!LtlSetEqual(set, set2)) continue;
/* p \in F <-> q \in F */
if (!AutomatonPfairEquivQfair(A, state, otherstate)) continue;
/* Img(p) - {p,q} == Img(q) - {p,q} */
tbl2 = AutomatonVertexGetImg(A->G, otherstate);
tbl3 = st_init_table(st_ptrcmp, st_ptrhash);
st_insert(tbl3, state, state);
st_insert(tbl3, otherstate, otherstate);
flag = StTableIsEqual(tbl1, tbl2, tbl3);
st_free_table(tbl3);
if (!flag) {
st_free_table(tbl2);
continue;
}
/* q \in delta(p) + p \in delta(p)] <->
* q \in delta(q) + p \in delta(q)]
*/
flag = 0;
if ( (st_is_member(tbl1, state) ||
st_is_member(tbl1, otherstate))
!=
(st_is_member(tbl2, state) ||
st_is_member(tbl2, otherstate)) ) {
st_free_table(tbl2);
continue;
}
/* ######## (state, otherstate) :: output compatible #######
* Merge the two state by deleting 'state'
* Notice that now we have the following data:
* tbl0 = PreImg(state)
* tbl1 = Img(state)
* tbl2 = Img(otherstate)
*/
tbl3 = AutomatonVertexGetPreImg(A->G, otherstate);
/* Add 'otherstate to Q0 if 'state' is in it */
if (st_is_member(A->Init, state)) {
st_delete(A->Init, &state, NIL(char *));
if(!st_is_member(A->Init, otherstate))
st_insert(A->Init, otherstate, otherstate);
}
/* Add edge (s, otherstate) where 's' is in PreImg(state) */
st_foreach_item(tbl0, stgen, &s, NIL(char *)) {
if (s != state && s != otherstate &&
!st_is_member(tbl3, s))
g_add_edge(s, otherstate);
}
/* Add edge (otherstate, otherstate) if there exist (state, state) or
* (state, otherstate)
*/
if (st_is_member(tbl1, otherstate) ||
st_is_member(tbl1, state))
if (!st_is_member(tbl2, otherstate))
g_add_edge(otherstate, otherstate);
/* Update don't care conditions. If 'state' isn't in dontcare, also
* remove 'otherstate'
*/
if (!st_is_member(A->dontcare, state)) {
StTableDelete(A->dontcare, (char *)otherstate);
}
StTableDelete(A->dontcare, (char *)state);
/* Remove 'state' from FairSets */
lsForEachItem (A->Fair, lsgen3, FairSet) {
StTableDelete(FairSet, (char *)state);
}
/* Remove 'state' from the automaton */
g_delete_vertex(state, Ltl_AutomatonNodeFree, (void(*)(gGeneric))0);
st_free_table(tbl2);
st_free_table(tbl3);
/* terminate iteration on incand list */
changed = localchanged = 1;
lsFinish(lsgen2);
break;
}
if (localchanged) {
lsDestroy(outcand, (void (*)(lsGeneric)) 0);
st_free_table(tbl0);
st_free_table(tbl1);
continue;
}
/* ############################
* Check for Dominance
* ############################
* We already have the lsList 'outcand'
*/
lsForEachItem (outcand, lsgen2, otherstate) {
/* p != q */
if (state == otherstate) continue;
/* L(p) \leq L(q) (set(Lp) > set(Lq) */
set = LtlAutomatonVertexGetLabels(state);
set2 = LtlAutomatonVertexGetLabels(otherstate);
if (!LtlSetInclude(set, set2)) continue;
/* p \in Q0 -> q \in Q0 */
if (st_is_member(A->Init, state) &&
!st_is_member(A->Init, otherstate))
continue;
/* p \in F -> q \in F */
if (!AutomatonPfairImplyQfair(A, state, otherstate)) continue;
/* Img(p) is less than Img(q) */
tbl2 = AutomatonVertexGetImg(A->G, otherstate);
flag = StTableInclude(tbl2, tbl1, NIL(st_table));
/* p is in Img(p) -> q is in Img(q) */
if (flag) {
flag = (!st_is_member(tbl1, state) ||
st_is_member(tbl2, otherstate));
}
st_free_table(tbl2);
if (!flag) continue;
/* PreImg(p)-{p} \leq PreImg(q)-{p} */
tbl3 = AutomatonVertexGetPreImg(A->G, otherstate);
tbl4 = st_init_table(st_ptrcmp, st_ptrhash);
st_insert(tbl4, state, state);
flag = StTableInclude(tbl3, tbl0, tbl4);
st_free_table(tbl4);
st_free_table(tbl3);
if (!flag) continue;
/* ######## otherstate dominates state #######
* Remove 'state'
* Notice that now we have the following data:
* tbl0 = PreImg(state)
* tbl1 = Img(state)
*/
/* Remove 'state' from Initial states */
StTableDelete(A->Init, (char *)state);
/* Remove 'otherstate' if 'state' isn't in dontcare */
if (!st_is_member(A->dontcare, state)) {
StTableDelete(A->dontcare, (char *)otherstate);
}
StTableDelete(A->dontcare, (char *)state);
/* Remove 'state' from FairSets */
lsForEachItem (A->Fair, lsgen3, FairSet) {
StTableDelete(FairSet, (char *)state);
}
/* Remove 'state' from the automaton */
g_delete_vertex(state, Ltl_AutomatonNodeFree, (void(*)(gGeneric))0);
/* terminate iteration on incand list */
changed = localchanged = 1;
lsFinish(lsgen2);
break;
}
lsDestroy(outcand, (void (*)(lsGeneric)) 0);
st_free_table(tbl0);
st_free_table(tbl1);
}
lsDestroy(states, (void (*)(lsGeneric)) 0);
return changed;
}
Here is the call graph for this function:
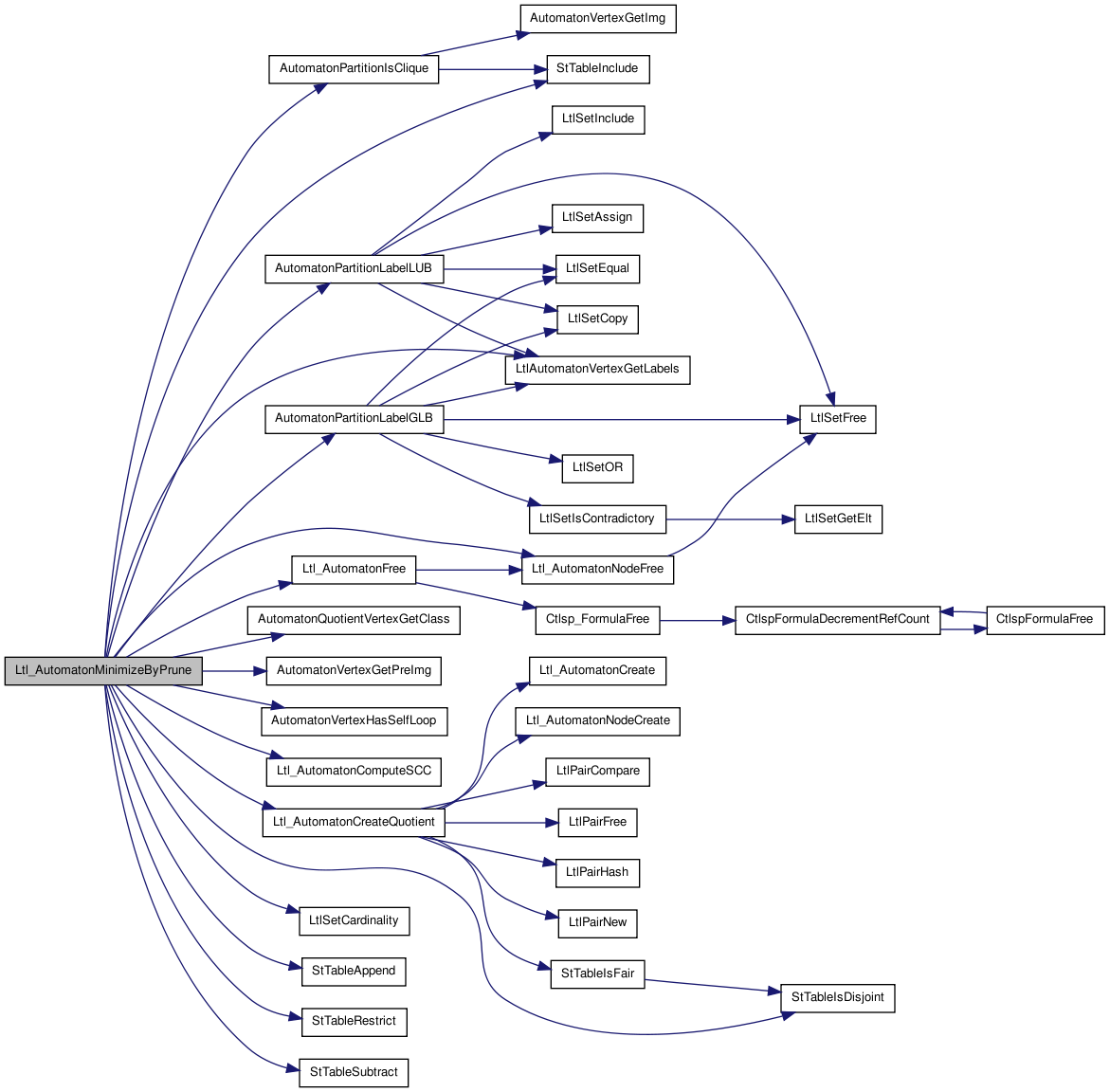
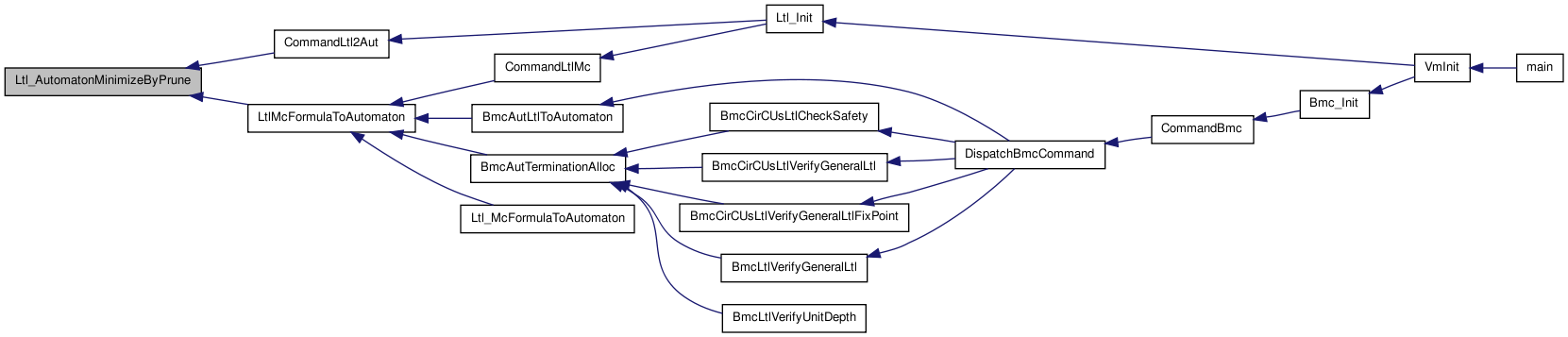
Here is the caller graph for this function:
| int Ltl_AutomatonMinimizeByPrune | ( | Ltl_Automaton_t * | A, |
| int | verbosity | ||
| ) |
Function********************************************************************
Synopsis [Remove states that cannot reach any fair SCC and perform other simplifications (simplify fair sets).]
Description [We consider the following cases concerning fair SCCs: 1. Remove redundant transitions from predecessors of universal states (a state with TRUE label and a self-loop, and it belongs to all fair sets.) 2. Remove all states that can not reach any fair SCC 3. Remove duplicate fair set and Shrink the fair sets ]
SideEffects [The automaton might be changed, in which case return 1. Also, the A->SCC and A->Q are RE-computed.]
SeeAlso []
Definition at line 1083 of file ltlMinimize.c.
{
st_generator *stgen, *stgen1, *stgen2;
st_table *FairSet, *otherset, *Class, *scc, *rest;
st_table *tbl, *tbl1, *tbl2;
lsList states, list;
lsGen lsgen, lsgen1;
vertex_t *state, *s, *greatest, *qstate;
edge_t *e;
long isFair;
int flag, totalnum, procnum;
/* Eliminate redundant edges from the predecessors of universal states.
* (A universal state is a state labeled 'TRUE' with a self-loop, and it
* should belong to all FairSets)
*/
states = lsCopy(g_get_vertices(A->G), (lsGeneric (*)(lsGeneric)) NULL);
lsForEachItem (states, lsgen, state) {
/* label = TRUE */
if (LtlSetCardinality(LtlAutomatonVertexGetLabels(state)) != 0)
continue;
/* self-loop */
if (!AutomatonVertexHasSelfLoop(A->G, state)) continue;
/* blongs to all fairSet */
flag = 1;
lsForEachItem (A->Fair, lsgen1, FairSet) {
if (!st_is_member(FairSet, state)) {
flag = 0;
lsFinish(lsgen1);
break;
}
}
if (!flag) continue;
/* We can apply the theorem: Remove edges from its predecessors to
* other siblings
*/
tbl = AutomatonVertexGetPreImg(A->G, state);
st_foreach_item(tbl, stgen, &s, NIL(char *)) {
if (s == state) continue;
list = lsCopy(g_get_out_edges(s), (lsGeneric (*)(lsGeneric))0);
lsForEachItem(list, lsgen1, e) {
if (g_e_dest(e) != state)
g_delete_edge(e, (void (*)(gGeneric))0);
}
lsDestroy(list, (void (*)(lsGeneric))0);
}
st_free_table(tbl);
}
/*2) Compute all the SCCs, and build the SCC-quotient graph
* every time before pruning, we need to re-compute the SCC graph
*/
Ltl_AutomatonComputeSCC(A, 1);
if (A->Q) {
Ltl_AutomatonFree((gGeneric) A->Q);
A->Q = NIL(Ltl_Automaton_t);
}
A->Q = Ltl_AutomatonCreateQuotient(A, A->SCC);
/* Mark those states without loop going through as "don't care states" */
st_foreach_item(A->SCC, stgen, &Class, &isFair) {
if (isFair == 2)
StTableAppend(A->dontcare, Class);
}
/* Restrict automaton to those states that can reach a fair SCC
* There are two cases: (a) with fairness (b) without fairness
*/
lsFirstItem(A->Q->Fair, &FairSet, NIL(lsHandle));
if (lsLength(A->Fair) > 0) {
/* (a) */
tbl = st_init_table(st_ptrcmp, st_ptrhash);
/* Find states that are on fair cycles */
st_foreach_item(FairSet, stgen, &qstate, NIL(char *)) {
Class = AutomatonQuotientVertexGetClass(qstate);
StTableAppend(tbl, Class);
}
/* Shrink fair sets in A->Fair */
lsForEachItem (A->Fair, lsgen, FairSet) {
StTableRestrict(FairSet, tbl);
}
/* Find states that can reach fair cycles */
tbl1 = tbl;
tbl = g_EF(A->G, tbl);
st_free_table(tbl1);
/* Remove the rest part of A->G */
StTableRestrict(A->Init, tbl);
StTableRestrict(A->dontcare, tbl);
lsForEachItem (states, lsgen, state) {
if (!st_is_member(tbl, state))
g_delete_vertex(state, Ltl_AutomatonNodeFree, (void(*)(gGeneric))0);
}
}else {
/* (b) */
/* Find all the reachable state */
tbl = g_reachable(A->G, A->Init);
/* Remove the rest part of A->G */
StTableRestrict(A->Init, tbl);
StTableRestrict(A->dontcare, tbl);
lsForEachItem (states, lsgen, state) {
if (!st_is_member(tbl, state))
g_delete_vertex(state, Ltl_AutomatonNodeFree, (void(*)(gGeneric))0);
}
}
/* Clean up the Quotient graph */
st_foreach_item(A->SCC, stgen, &Class, &isFair) {
StTableRestrict(Class, tbl);
}
st_free_table(tbl);
/* 3. Remove duplicate FairSet */
/* Discard duplicate fair sets and fair sets including all states. Here we
* also restrict fair sets by analyzing each SCC. If within an SCC, one fair
* set dominates another, it can be restricted to the dominated one. As a
* special case: if an SCC does not intersect all fair sets, its states are
* removed from all fair sets.
*/
totalnum = lsLength(A->Fair);
procnum = 0;
while(lsDelBegin(A->Fair, &FairSet) != LS_NOMORE) {
/* Remove this FairSet if it includes all states in the SCC */
if (st_count(FairSet) == lsLength(g_get_vertices(A->G))) {
st_free_table(FairSet);
totalnum--;
}else {
/* After restricted to the SCC: if fair set2 is contained in set1,
* shrink set1 to set2 (remove (set1-set2) from set1
*/
st_foreach_item(A->SCC, stgen, &scc, &isFair) {
lsForEachItem(A->Fair, lsgen, otherset) {
tbl1 = st_copy(scc);
tbl2 = st_copy(scc);
StTableRestrict(tbl1, FairSet);
StTableRestrict(tbl2, otherset);
if (StTableInclude(tbl1, tbl2, NIL(st_table))) {
/* tbl1 <= (tbl1 - tbl2) */
StTableSubtract(tbl1, tbl2);
StTableSubtract(FairSet, tbl1);
}
st_free_table(tbl1);
st_free_table(tbl2);
}
}
/* Remove the fair set if another fair set is contained in it */
flag = 1;
lsForEachItem(A->Fair, lsgen, otherset) {
if (StTableInclude(FairSet,otherset,NIL(st_table))) {
flag = 0;
lsFinish(lsgen);
break;
}
}
if (!flag) {
st_free_table(FairSet);
totalnum--;
}else
lsNewEnd(A->Fair, (lsGeneric) FairSet, NIL(lsHandle));
}
procnum++;
if (procnum > totalnum) break;
}
/* 4. GLB reduction */
/* If an SCC is a clique, and there is a state 's' whose label exactly matches
* the GLB of all the labels of the clique, we can remove 's' from every fair
* set such that it contains at least another state of the SCC besides 's'
*/
st_foreach_item(A->SCC, stgen, &Class, &isFair) {
/* 1-state SCC won't work */
if (st_count(Class) <= 1) continue;
/* must be a clique */
if (!AutomatonPartitionIsClique(A->G, Class)) continue;
tbl = AutomatonPartitionLabelGLB(Class, A->labelTableNegate);
if (!tbl) continue;
rest = st_copy(Class);
StTableSubtract(rest, tbl);
lsForEachItem(A->Fair, lsgen, FairSet) {
if (StTableInclude(FairSet, tbl, NIL(st_table)) &&
!StTableIsDisjoint(FairSet, rest, NIL(st_table)))
/* we apply the theorem here */
StTableSubtract(FairSet, tbl);
}
st_free_table(rest);
st_free_table(tbl);
}
/* 5. LUB reduction */
/* If an SCC contains a state 's' that simulates all the other states in the
* same SCC (both forward and backward), then all states of the SCC except
* 's' can be removed from all fair sets. The following code checks for a
* special case of this theorem
*/
st_foreach_item(A->SCC, stgen, &Class, &isFair) {
vertex_t *qstate;
st_lookup(A->Q->SCC, Class, &qstate);
/* 1-state SCC won't work */
if (st_count(Class) <= 1) continue;
tbl = AutomatonPartitionLabelLUB(Class, A->labelTableNegate);
if (!tbl) continue;
st_foreach_item(tbl, stgen1, &greatest, NIL(char *)) {
/* that state should have a self-loop */
if (!AutomatonVertexHasSelfLoop(A->G, greatest)) continue;
/* that state should be initial if the SCC contains initial states */
if (st_is_member(A->Q->Init, qstate) &&
!st_is_member(A->Init, greatest))
continue;
/* that state should belong to FairSet if the SCC intersect it */
flag = 1;
lsForEachItem(A->Fair, lsgen, FairSet) {
if (!st_is_member(FairSet, greatest) &&
!StTableIsDisjoint(FairSet,Class,NIL(st_table))){
flag = 0;
lsFinish(lsgen);
break;
}
}
if (!flag) continue;
/* Every state outside of the SCC with a transition into the SCC
* should also have a transition to that state
*/
tbl1 = st_init_table(st_ptrcmp, st_ptrhash);
st_foreach_item(Class, stgen2, &state, NIL(char *)) {
tbl2 = AutomatonVertexGetPreImg(A->G, state);
StTableAppend(tbl1, tbl2);
st_free_table(tbl2);
}
tbl2 = AutomatonVertexGetPreImg(A->G, greatest);
flag = StTableInclude(tbl2, tbl1, Class);
st_free_table(tbl2);
st_free_table(tbl1);
if (!flag) continue;
/* we now apply the theorem */
tbl1 = st_copy(Class);
if (st_is_member(tbl1, greatest))
st_delete(tbl1, &greatest, NIL(char *));
lsForEachItem(A->Fair, lsgen, FairSet) {
StTableSubtract(FairSet, tbl1);
}
st_free_table(tbl1);
}
st_free_table(tbl);
}
lsDestroy(states, (void (*)(lsGeneric))0);
return 1;
}
Here is the call graph for this function:
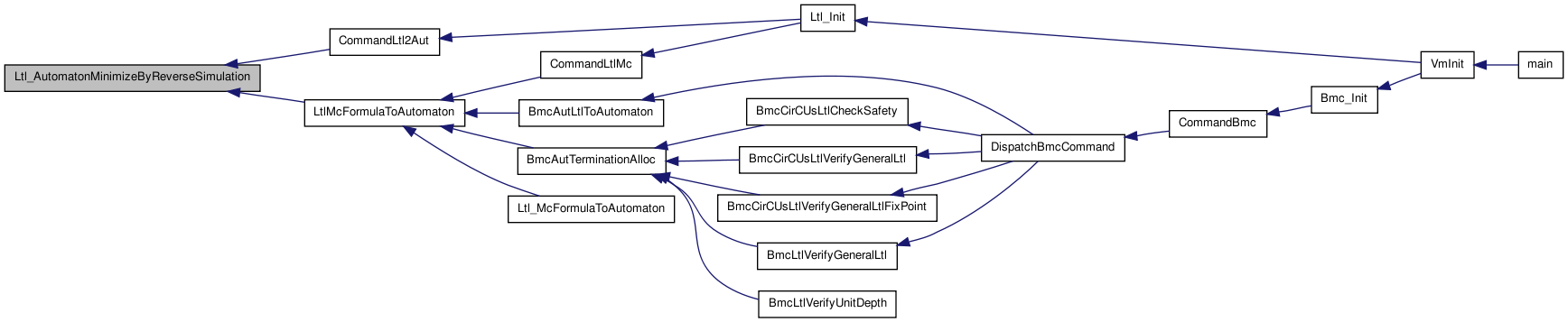
Here is the caller graph for this function:
| int Ltl_AutomatonMinimizeByReverseSimulation | ( | Ltl_Automaton_t * | A, |
| int | verbosity | ||
| ) |
Function********************************************************************
Synopsis [Minimize the Automaton using Reverse Simulation.]
Description [Compute Reverse-Simulation relation, and minimize the automaton according to the following 2 cases: 1) remove p if (p,q) is a Bi-Simulation relation 2) remove edges from p to their common sucessors if p is reverse simulated by q.]
SideEffects [The automaton might be changed. if so, return 1.]
SeeAlso []
Definition at line 849 of file ltlMinimize.c.
{
int changed = 0;
int flag = 0;
lsList states, otherstates, list, queue;
lsGen lsgen, lsgen1;
edge_t *e;
vertex_t *state, *otherstate;
vertex_t *p, *q, *s, *t, *u, *v;
LtlSet_t *set, *set2;
st_table *FairSet, *tbl0, *tbl1, *tbl2, *tbl3;
st_table *simul, *enqueued;
st_generator *stgen, *stgen1, *stgen2;
LtlPair_t *pair, *pair2;
/* store the simulation-relation in hash tables and queue list */
simul = st_init_table(LtlPairCompare, LtlPairHash);
enqueued = st_init_table(LtlPairCompare, LtlPairHash);
queue = lsCreate();
/*######################################
* Initialize sim rln to all pairs (p,q)
*######################################
*/
states = lsCopy(g_get_vertices(A->G), (lsGeneric (*)(lsGeneric)) NULL);
otherstates = lsCopy(states, (lsGeneric (*)(lsGeneric)) NULL);
lsForEachItem (states, lsgen, state) {
lsForEachItem (otherstates, lsgen1, otherstate) {
/* p != q */
if (state == otherstate) continue;
/* L(p) <= L(q), in other words, (set(Lp) >= set(Lq) */
set = LtlAutomatonVertexGetLabels(state);
set2 = LtlAutomatonVertexGetLabels(otherstate);
if (!LtlSetInclude(set, set2)) continue;
/* p is in Q0 -> q is in Q0 */
if (st_is_member(A->Init, state) &&
!st_is_member(A->Init, otherstate))
continue;
/* p is in F -> q is in F */
if (!AutomatonPfairImplyQfair(A, state, otherstate)) continue;
/* put (state, otherstate) into simul-relation */
pair = LtlPairNew((char *)state, (char *)otherstate);
st_insert(simul, pair, pair);
st_insert(enqueued, pair, pair);
lsNewEnd(queue, (lsGeneric)pair, NIL(lsHandle));
}
}
lsDestroy(states, (void (*)(lsGeneric)) NULL);
lsDestroy(otherstates, (void (*)(lsGeneric)) NULL);
/*######################################
* Compute the "Greatest Fixpoint"
*######################################
*/
while (lsDelBegin(queue, &pair) != LS_NOMORE) {
st_delete(enqueued, &pair, NIL(char *));
p = (vertex_t *)pair->First;
q = (vertex_t *)pair->Second;
/* For each 's' in Img(p), there must exists a 't' Img(q) such that
* (s, t) is also a reverse simulation pair
*/
tbl0 = AutomatonVertexGetPreImg(A->G, p);
tbl1 = AutomatonVertexGetPreImg(A->G, q);
st_foreach_item(tbl0, stgen, &s, NIL(char *)) {
flag = 0;
st_foreach_item(tbl1, stgen1, &t, NIL(char *)) {
flag = (s==t);
if (flag) {
st_free_gen(stgen1);
break;
}
pair2 = LtlPairNew((char *)s, (char *)t);
flag = st_is_member(simul, pair2);
LtlPairFree(pair2);
if (flag) {
st_free_gen(stgen1);
break;
}
}
if (!flag) {
st_free_gen(stgen);
break;
}
}
st_free_table(tbl0);
st_free_table(tbl1);
if (flag) continue;
/* (p, q) is not a simulation relation */
st_delete(simul, &pair, &pair);
LtlPairFree(pair);
/* Enqueue perturbed pairs */
tbl2 = AutomatonVertexGetImg(A->G, p);
tbl3 = AutomatonVertexGetImg(A->G, q);
st_foreach_item(tbl2, stgen1, &u, NIL(char *)) {
st_foreach_item(tbl3, stgen2, &v, NIL(char *)) {
pair2 = LtlPairNew((char *)u, (char *)v);
if (st_lookup(simul, pair2, &pair))
if(!st_is_member(enqueued, pair2)) {
st_insert(enqueued, pair, pair);
lsNewEnd(queue, (lsGeneric)pair, NIL(lsHandle));
}
LtlPairFree(pair2);
}
}
st_free_table(tbl2);
st_free_table(tbl3);
}
lsDestroy(queue, (void (*)(lsGeneric))0);
st_free_table(enqueued);
/*######################################
* Simplify by Bi-Sim equivalent states
*######################################
*/
/* to store removed states */
tbl1 = st_init_table(st_ptrcmp, st_ptrhash);
/* so that we can modify simul with the for loop */
tbl0 = st_copy(simul);
st_foreach_item (tbl0, stgen, &pair, NIL(char *)) {
p = (vertex_t *)pair->First;
q = (vertex_t *)pair->Second;
/* Make sure neither has been removed */
if (st_is_member(tbl1, p) || st_is_member(tbl1, q))
continue;
/* Make sure it is Bi-simulation by checking the other direction*/
pair2 = LtlPairNew((char *)q, (char *)p);
flag = st_lookup(simul, pair2, &pair);
LtlPairFree(pair2);
if (!flag) continue;
/*#### Direct BI-SIMULATION equivalent states####*/
/* Theorem applies */
/* Remove its swap: (q, p) from simul-rln */
st_delete(simul, &pair, &pair);
LtlPairFree(pair);
/* Remove 'p' and connect 'q' to all its successors */
tbl2 = AutomatonVertexGetImg(A->G, p);
tbl3 = AutomatonVertexGetImg(A->G, q);
st_foreach_item(tbl2, stgen1, &s, NIL(char *)) {
if (s == p) continue;
if (!st_is_member(tbl3, s))
g_add_edge(q, s);
}
st_free_table(tbl2);
st_free_table(tbl3);
/* Update the fairsets (remove 'p') */
lsForEachItem (A->Fair, lsgen, FairSet) {
StTableDelete(FairSet, (char *)p);
}
/* Remove 'p' from Q0 */
StTableDelete(A->Init, (char *)p);
/* Remove 'p' form dontcare if it's in it */
StTableDelete(A->dontcare, (char *)p);
/* Remove 'p' from the automaton */
st_insert(tbl1, p, p);
g_delete_vertex(p, Ltl_AutomatonNodeFree, (void(*)(gGeneric))0);
changed = 1;
}
st_free_table(tbl0);
/*######################################
* Remove arcs from Reverse-simulated states
*#####################################*/
/* so that we can modify simul with the for loop */
tbl0 = st_copy(simul);
st_foreach_item (tbl0, stgen, &pair, NIL(char *)) {
/* 'p' is simulated by 'q' */
p = (vertex_t *)pair->First;
q = (vertex_t *)pair->Second;
/* Make sure that neither has been removed */
if (st_is_member(tbl1, p) || st_is_member(tbl1, q))
continue;
/*#### p is reverse-simulated by q####*/
/* Theorem applies */
/* Drop arcs from 'p' to their common successors */
tbl3 = AutomatonVertexGetImg(A->G, q);
list = lsCopy(g_get_out_edges(p), (lsGeneric (*)(lsGeneric)) NULL);
lsForEachItem (list, lsgen, e) {
if (!st_is_member(tbl3, g_e_dest(e))) continue;
g_delete_edge(e, (void (*)(gGeneric))0);
changed = 1;
}
lsDestroy(list, (void (*)(lsGeneric)) 0);
st_free_table(tbl3);
}
st_free_table (tbl0);
st_free_table (tbl1);
st_foreach_item(simul, stgen, &pair, NIL(char *)) {
LtlPairFree(pair);
}
st_free_table (simul);
return changed;
}
Here is the call graph for this function:
Here is the caller graph for this function:
| int Ltl_AutomatonVtxGetNodeIdx | ( | vertex_t * | v | ) |
Function********************************************************************
Synopsis [Return the node index associated with the given vertex.]
SideEffects []
Definition at line 1690 of file ltlMinimize.c.
{
Ltl_AutomatonNode_t *node = (Ltl_AutomatonNode_t *) v->user_data;
return node->index;
}
Here is the caller graph for this function:
| LtlSet_t* LtlAutomatonVertexGetLabels | ( | vertex_t * | vtx | ) |
Function********************************************************************
Synopsis [Return the automaton node label set associated with the vertex.]
SideEffects [The result is owned by the node, and should not be freed.]
Definition at line 1705 of file ltlMinimize.c.
{
Ltl_AutomatonNode_t *node = (Ltl_AutomatonNode_t *) vtx->user_data;
return node->Labels;
}
Here is the caller graph for this function:
| static st_table * StTableAppend | ( | st_table * | tbl1, |
| st_table * | tbl2 | ||
| ) | [static] |
Function********************************************************************
Synopsis [Append the tbl2 to tbl1 and return tbl1.]
SideEffects [tbl1 is permenently changed.]
Definition at line 2006 of file ltlMinimize.c.
{
char *key, *value;
st_generator *stgen;
st_foreach_item(tbl2, stgen, &key, &value) {
if (!st_is_member(tbl1, key))
st_insert(tbl1, key, value);
}
return tbl1;
}
Here is the caller graph for this function:
| static char * StTableDelete | ( | st_table * | tbl, |
| char * | item | ||
| ) | [static] |
Function********************************************************************
Synopsis [If 'item' is in the hash table, Delete it and return the real key; Otherwise, return 0.]
SideEffects ['item' will not be modified.]
Definition at line 1985 of file ltlMinimize.c.
{
char *key = item;
if (st_is_member(tbl, key)) {
st_delete(tbl, &key, NIL(char *));
return key;
}else
return NIL(char);
}
Here is the caller graph for this function:
| static int StTableInclude | ( | st_table * | large, |
| st_table * | small, | ||
| st_table * | dontcare | ||
| ) | [static] |
Function********************************************************************
Synopsis [Return 1 if 'larger' include every items in 'small' except those also in 'dontcare'. Notice that 'dontcare' can be a null pointer.]
SideEffects []
Definition at line 2122 of file ltlMinimize.c.
{
int flag = 1;
st_generator *stgen;
vertex_t *vtx;
flag = 1;
st_foreach_item(small, stgen, &vtx, NIL(char *)) {
if (dontcare) {
if (st_is_member(dontcare, vtx)) continue;
}
if (!st_is_member(large,vtx)) {
flag = 0;
st_free_gen(stgen);
break;
}
}
return flag;
}
Here is the caller graph for this function:
| static int StTableIsDisjoint | ( | st_table * | tbl1, |
| st_table * | tbl2, | ||
| st_table * | dontcare | ||
| ) | [static] |
Function********************************************************************
Synopsis [Return 1 if the two tables shares nothing except those items also in 'dontcare'. Notice that 'dontcare' can be a null pointer.]
SideEffects []
Definition at line 2156 of file ltlMinimize.c.
{
int flag = 1;
st_generator *stgen;
vertex_t *vtx;
flag = 1;
st_foreach_item(tbl1, stgen, &vtx, NIL(char *)) {
if (dontcare) {
if (st_is_member(dontcare, vtx)) continue;
}
if (st_is_member(tbl2,vtx)) {
flag = 0;
st_free_gen(stgen);
break;
}
}
if (!flag) return 0;
st_foreach_item(tbl2, stgen, &vtx, NIL(char *)) {
if (dontcare) {
if (st_is_member(dontcare, vtx)) continue;
}
if (st_is_member(tbl1,vtx)) {
flag = 0;
st_free_gen(stgen);
break;
}
}
return flag;
}
Here is the caller graph for this function:
| static int StTableIsEqual | ( | st_table * | tbl1, |
| st_table * | tbl2, | ||
| st_table * | dontcare | ||
| ) | [static] |
Function********************************************************************
Synopsis [Return 1 if tbl1 and tbl2 have the same items except those also in 'dontcare'. 'dontcare' can be a null pointer.]
SideEffects []
Definition at line 2078 of file ltlMinimize.c.
{
int flag = 1;
st_generator *stgen;
vertex_t *vtx;
flag = 1;
st_foreach_item(tbl1, stgen, &vtx, NIL(char *)) {
if (dontcare) {
if (st_is_member(dontcare,vtx)) continue;
}
if (!st_is_member(tbl2,vtx)) {
flag = 0;
st_free_gen(stgen);
break;
}
}
if (!flag) return 0;
st_foreach_item(tbl2, stgen, &vtx, NIL(char *)) {
if (dontcare) {
if (st_is_member(dontcare,vtx)) continue;
}
if (!st_is_member(tbl1, vtx)) {
flag = 0;
st_free_gen(stgen);
break;
}
}
return flag;
}
Here is the caller graph for this function:
| static int StTableIsFair | ( | lsList | A_Fair, |
| st_table * | Class | ||
| ) | [static] |
Function********************************************************************
Synopsis [Return 1 if the given tables intersect every tables in the list.]
SideEffects []
Definition at line 2199 of file ltlMinimize.c.
{
int flag;
st_table *FairSet;
lsGen lsgen;
flag = 1;
lsForEachItem (A_Fair, lsgen, FairSet) {
if (StTableIsDisjoint(FairSet,Class,NIL(st_table))) {
flag = 0;
lsFinish(lsgen);
break;
}
}
return flag;
}
Here is the call graph for this function:
Here is the caller graph for this function:
| static st_table * StTableRestrict | ( | st_table * | tbl1, |
| st_table * | tbl2 | ||
| ) | [static] |
Function********************************************************************
Synopsis [Remove from tbl1 all the items that are not in tbl2.]
SideEffects [tbl1 is changed and returned.]
Definition at line 2029 of file ltlMinimize.c.
{
char *key, *value;
st_table *tbl = st_copy(tbl1);
st_generator *stgen;
st_foreach_item(tbl, stgen, &key, &value) {
if (!st_is_member(tbl2, key))
st_delete(tbl1, &key, &value);
}
st_free_table(tbl);
return tbl1;
}
Here is the caller graph for this function:
| static st_table * StTableSubtract | ( | st_table * | tbl1, |
| st_table * | tbl2 | ||
| ) | [static] |
Function********************************************************************
Synopsis [Remove from tbl1 all the items that are in tbl2.]
SideEffects [tbl1 is changed and returned.]
Definition at line 2054 of file ltlMinimize.c.
{
char *key, *value;
st_generator *stgen;
st_foreach_item(tbl2, stgen, &key, &value) {
if (st_is_member(tbl1, key))
st_delete(tbl1, &key, &value);
}
return tbl1;
}
Here is the caller graph for this function:
Variable Documentation
char rcsid [] UNUSED = "$Id: ltlMinimize.c,v 1.33 2009/04/09 02:21:13 fabio Exp $" [static] |
CFile***********************************************************************
FileName [ltlMinimize.c]
PackageName [ltl]
Synopsis [Buechi automaton minimization.]
Author [Chao Wang<chao.wang@colorado.EDU>]
Copyright [This file was created at the University of Colorado at Boulder. The University of Colorado at Boulder makes no warranty about the suitability of this software for any purpose. It is presented on an AS IS basis.]
Definition at line 19 of file ltlMinimize.c.
