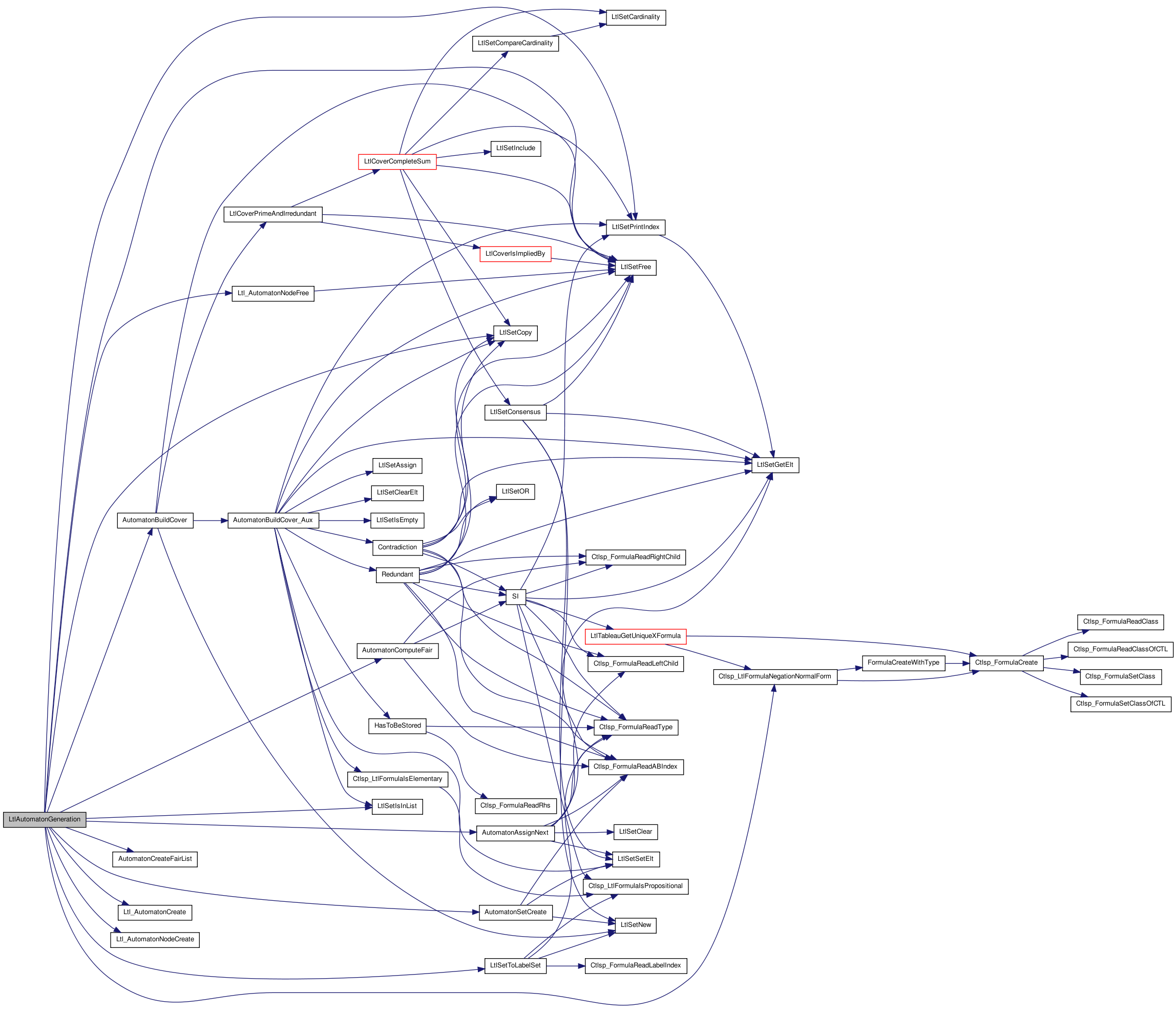
#include "ltlInt.h" Include dependency graph for ltlAutomaton.c:
Include dependency graph for ltlAutomaton.c:Go to the source code of this file.
Functions | |
| static int | HasToBeStored (LtlTableau_t *tableau, int index) |
| static int | Contradiction (LtlTableau_t *tableau, int index, LtlSet_t *ToCover, LtlSet_t *Current, LtlSet_t *Covered) |
| static int | Redundant (LtlTableau_t *tableau, int index, LtlSet_t *ToCover, LtlSet_t *Current, LtlSet_t *Covered) |
| static int | SI (LtlTableau_t *tableau, int index, LtlSet_t *A) |
| static void | AutomatonComputeFair (LtlTableau_t *tableau, LtlSet_t *r, vertex_t *vtx1) |
| static int | AutomatonCreateFairList (LtlTableau_t *tableau, Ltl_Automaton_t *aut) |
| static void | AutomatonAssignNext (LtlTableau_t *tableau, LtlSet_t *toCover, LtlSet_t *s) |
| static LtlSet_t * | AutomatonSetCreate (LtlTableau_t *tableau, Ctlsp_Formula_t *F) |
| static lsList | AutomatonBuildCover (LtlTableau_t *tableau, LtlSet_t *ToCover) |
| static void | AutomatonBuildCover_Aux (LtlTableau_t *tableau, LtlSet_t *pToCover, LtlSet_t *pCurrent, LtlSet_t *pCovered, lsList Cover) |
| Ltl_Automaton_t * | Ltl_AutomatonCreate (void) |
| void | Ltl_AutomatonFree (gGeneric g) |
| Ltl_AutomatonNode_t * | Ltl_AutomatonNodeCreate (Ltl_Automaton_t *aut) |
| void | Ltl_AutomatonNodeFree (gGeneric g) |
| void | Ltl_AutomatonNodePrint (Ltl_Automaton_t *aut, Ltl_AutomatonNode_t *node) |
| void | Ltl_AutomatonPrint (Ltl_Automaton_t *aut, int verbosity) |
| Ltl_Automaton_t * | LtlAutomatonGeneration (LtlTableau_t *tableau) |
| int | LtlAutomatonSetIsFair (LtlTableau_t *tableau, LtlSet_t *r) |
Variables | |
| static char rcsid[] | UNUSED = "$Id: ltlAutomaton.c,v 1.34 2005/04/28 08:47:15 bli Exp $" |
Function Documentation
| static void AutomatonAssignNext | ( | LtlTableau_t * | tableau, |
| LtlSet_t * | toCover, | ||
| LtlSet_t * | s | ||
| ) | [static] |
Function********************************************************************
Synopsis [Generate the next-formulae set.]
Description [toCover = { u: X(u) is in s }. In other words, for each formula of the form X(u) in the set 's', add the subformula u into 'toCover'.]
SideEffects ['toCover' is changed.]
Definition at line 953 of file ltlAutomaton.c.
{
int i;
Ctlsp_FormulaType type;
Ctlsp_Formula_t *left;
int left_ab_idx;
LtlSetClear(toCover);
for (i=0; i<tableau->abIndex; i++) {
if (LtlSetGetElt(s, i)) {
type = Ctlsp_FormulaReadType(tableau->abTable[i].F);
if (type == Ctlsp_X_c) {
left = Ctlsp_FormulaReadLeftChild(tableau->abTable[i].F);
left_ab_idx = Ctlsp_FormulaReadABIndex(left);
LtlSetSetElt(toCover, left_ab_idx);
}
}
}
}
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:| static lsList AutomatonBuildCover | ( | LtlTableau_t * | tableau, |
| LtlSet_t * | ToCover | ||
| ) | [static] |
Function********************************************************************
Synopsis [Build the cover for a given set 'toCover'.]
Description [The cover is "a list of sets", where the sets are product terms and the list is in DNF form (union of all its product terms).]
SideEffects [The result should be freed by the caller.]
Definition at line 1015 of file ltlAutomaton.c.
{
LtlSet_t *Current = LtlSetNew(tableau->abIndex);
LtlSet_t *Covered = LtlSetNew(tableau->abIndex);
lsList Cover = lsCreate();
AutomatonBuildCover_Aux(tableau, ToCover, Current, Covered, Cover);
LtlSetFree(Current);
LtlSetFree(Covered);
/* Boolean Minimization -- heuristics */
if (tableau->booleanmin == 1) {
if (lsLength(Cover)) {
lsList list = Cover;
Cover = LtlCoverPrimeAndIrredundant(tableau, Cover,
tableau->abTableNegate);
lsDestroy(list, (void (*)(lsGeneric))LtlSetFree);
}
}
return Cover;
}
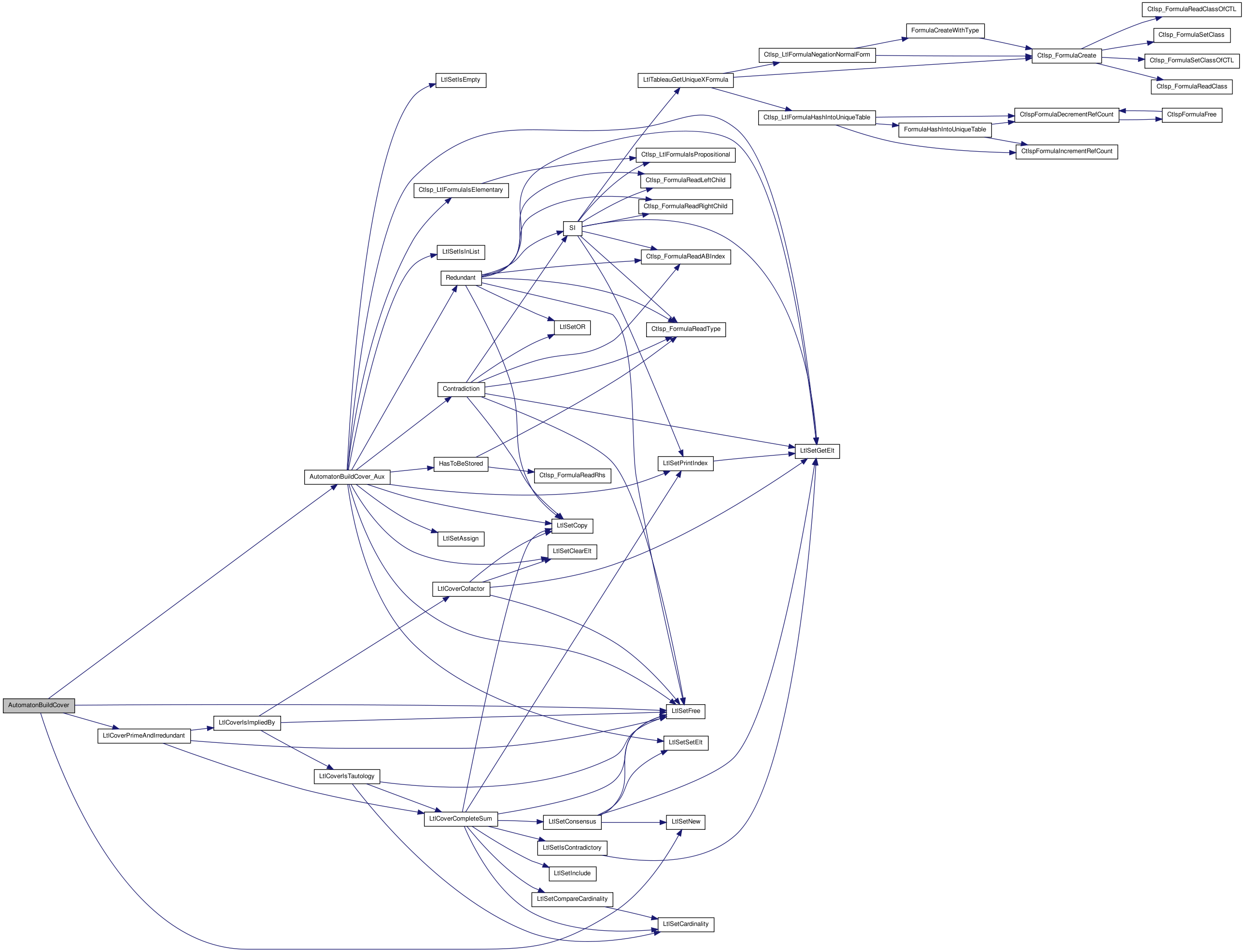
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:| static void AutomatonBuildCover_Aux | ( | LtlTableau_t * | tableau, |
| LtlSet_t * | pToCover, | ||
| LtlSet_t * | pCurrent, | ||
| LtlSet_t * | pCovered, | ||
| lsList | Cover | ||
| ) | [static] |
Function********************************************************************
Synopsis [Recursively construct the cover.]
Description [the cover is updated in the parameter 'lsList Cover'. This function is used in AutomatonBuildCover() only.]
SideEffects []
Definition at line 1050 of file ltlAutomaton.c.
{
LtlSet_t *ToCover = LtlSetCopy(pToCover);
LtlSet_t *Current = LtlSetCopy(pCurrent);
LtlSet_t *Covered = LtlSetCopy(pCovered);
int i;
#ifdef DEBUG_LTLMC
if (tableau->verbosity >2 ) {
fprintf(vis_stdout, "ToCover=");
LtlSetPrintIndex(tableau->abIndex, ToCover);
fprintf(vis_stdout, "Current=");
LtlSetPrintIndex(tableau->abIndex, Current);
fprintf(vis_stdout, "Covered=");
LtlSetPrintIndex(tableau->abIndex, Covered);
fflush(vis_stdout);
}
#endif
if (LtlSetIsEmpty(ToCover)) {
#if 1
/* chao: 7/22/2002 remove identical set in current Cover */
if (!LtlSetIsInList(Current, Cover))
#endif
lsNewEnd(Cover, (lsGeneric) LtlSetCopy(Current), (lsHandle *) 0);
/* return */
}else {
/* select 'u' from 'ToCover' */
for (i=0; i<tableau->abIndex; i++) {
if (LtlSetGetElt(ToCover,i))
break;
}
/* remove 'u' from 'ToCover' and add it to 'Covered' */
LtlSetClearElt(ToCover, i);
LtlSetSetElt(Covered, i);
/* if HAS_TO_BE_STORED(u), store into 'Current' */
if (HasToBeStored(tableau,i))
LtlSetSetElt(Current, i);
/* if CONTRADICTION(u, ToCover, Current, Covered), return 'Cover' */
if (Contradiction(tableau, i, ToCover, Current, Covered)) {
; /* return */
}else if (Redundant(tableau, i, ToCover, Current, Covered)) {
AutomatonBuildCover_Aux(tableau, ToCover, Current, Covered, Cover);
/* return */
}else {
if (Ctlsp_LtlFormulaIsElementary(tableau->abTable[i].F)) {
LtlSetSetElt(Current, i);
AutomatonBuildCover_Aux(tableau, ToCover, Current, Covered,
Cover);
/* return */
}else {
int A0B0 = tableau->abTable[i].A[0].B[0];
int A0B1 = tableau->abTable[i].A[0].B[1];
int A0n = tableau->abTable[i].A[0].n;
int A1B0 = tableau->abTable[i].A[1].B[0];
int A1B1 = tableau->abTable[i].A[1].B[1];
int A1n = tableau->abTable[i].A[1].n;
/* cover( (ToCover+alph2(u)-Current), Current, Covered, Cover) */
if (A1B0 != -1 || A1B1!= -1 || A1n!= -1) {
LtlSet_t *saveToCover = LtlSetCopy(ToCover);
if (A1B0 != -1)
if (!LtlSetGetElt(Current, A1B0))
LtlSetSetElt(ToCover, A1B0);
if (A1B1 != -1)
if (!LtlSetGetElt(Current, A1B1))
LtlSetSetElt(ToCover, A1B1);
if (A1n != -1)
if (!LtlSetGetElt(Current, A1n))
LtlSetSetElt(ToCover, A1n);
AutomatonBuildCover_Aux(tableau, ToCover, Current, Covered,
Cover);
LtlSetAssign(ToCover, saveToCover);
LtlSetFree(saveToCover);
}
/* cover( (ToCover+alph1(u)-Current), Current, Covered, Cover) */
if (A0B0 != -1 || A0B1!= -1 || A0n!= -1) {
if (A0B0 != -1)
if (!LtlSetGetElt(Current, A0B0))
LtlSetSetElt(ToCover, A0B0);
if (A0B1 != -1)
if (!LtlSetGetElt(Current, A0B1))
LtlSetSetElt(ToCover, A0B1);
if (A0n != -1)
if (!LtlSetGetElt(Current, A0n))
LtlSetSetElt(ToCover, A0n);
AutomatonBuildCover_Aux(tableau, ToCover, Current, Covered,
Cover);
}
/* return */
}
}
}
/* Clean-Ups */
LtlSetFree(ToCover);
LtlSetFree(Current);
LtlSetFree(Covered);
}
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:| static void AutomatonComputeFair | ( | LtlTableau_t * | tableau, |
| LtlSet_t * | r, | ||
| vertex_t * | vtx1 | ||
| ) | [static] |
Function********************************************************************
Synopsis [Put the node into the fairset if it contains a until formula.]
Description [Each until formula in the 'untilUnqiueTable' corresponds to a fair set (a set of vertices in the automaton, represented by a hash table. A vertex belongs to a fair set iff its cover set contains the until formula.]
SideEffects []
Definition at line 871 of file ltlAutomaton.c.
{
st_table *uniqueTable = tableau->untilUniqueTable;
char *key, *value;
st_generator *gen;
/* Notice that each pair in 'uniqueTable' is a (Unitl formula, Fair set) */
st_foreach_item(uniqueTable, gen, &key, &value) {
Ctlsp_Formula_t *F = (Ctlsp_Formula_t *) key;
Ctlsp_Formula_t *right = Ctlsp_FormulaReadRightChild(F);
int F_ab_idx = Ctlsp_FormulaReadABIndex(F);
int right_ab_idx = Ctlsp_FormulaReadABIndex(right);
lsList Fair = (lsList) value;
if ( SI(tableau, right_ab_idx, r) || !(SI(tableau, F_ab_idx, r)) ) {
lsNewEnd(Fair, (lsGeneric) vtx1, (lsHandle *) 0);
}
}
}
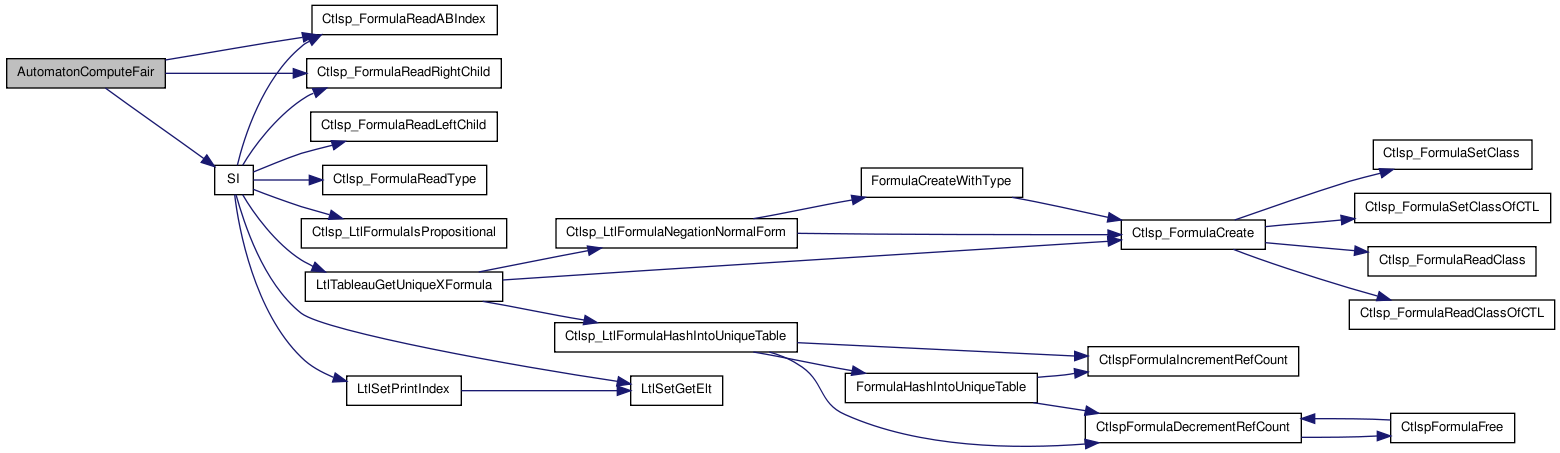
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:| static int AutomatonCreateFairList | ( | LtlTableau_t * | tableau, |
| Ltl_Automaton_t * | aut | ||
| ) | [static] |
Function********************************************************************
Synopsis [Convert the fair sets of the tableau into the fair set in the automaton.]
Description [The fairness in the tableau is "a hash table (Until formula, FairVerticesList)". The fairness in the automaton should be " a list of hash tables" (each hash table corresponds to a fair set, and a vertex is in the hash table iff it's in that fair set).
Return 0 iff there is an empty fairset (which means the language of the automaton is empty no matter what); Return 1 otherwise.]
SideEffects []
Definition at line 911 of file ltlAutomaton.c.
{
lsList FairList = aut->Fair;
char *key, *value;
st_generator *gen;
int noEmptyFairSet = 1;
st_foreach_item(tableau->untilUniqueTable, gen, &key, &value) {
lsList Fair = (lsList) value;
/* translate a lsList into a st_table */
if (lsLength(Fair) > 0) {
lsGen lsgen;
lsGeneric lsdata;
st_table *tbl = st_init_table(st_ptrcmp, st_ptrhash);
lsForEachItem (Fair, lsgen, lsdata) {
st_insert(tbl, lsdata, lsdata);
}
lsNewEnd(FairList, (lsGeneric) tbl, (lsHandle *) 0);
}else
noEmptyFairSet = 0;
lsDestroy(Fair, (void (*)(lsGeneric)) NULL);
}
return noEmptyFairSet;
}
 Here is the caller graph for this function:
Here is the caller graph for this function:| static LtlSet_t * AutomatonSetCreate | ( | LtlTableau_t * | tableau, |
| Ctlsp_Formula_t * | F | ||
| ) | [static] |
Function********************************************************************
Synopsis [Create the set representation of the given formula.]
Description [Its size will be the total number of sub-formulae in the tableau. Only the bit corresponding to the given formula is set.]
SideEffects [The result should be freed by the caller.]
Definition at line 990 of file ltlAutomaton.c.
{
LtlSet_t *cs = LtlSetNew(tableau->abIndex);
if (!F)
return cs;
LtlSetSetElt(cs, Ctlsp_FormulaReadABIndex(F));
return cs;
}
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:| static int Contradiction | ( | LtlTableau_t * | tableau, |
| int | index, | ||
| LtlSet_t * | ToCover, | ||
| LtlSet_t * | Current, | ||
| LtlSet_t * | Covered | ||
| ) | [static] |
Function********************************************************************
Synopsis [Return 1 iff there is there is a contradition so far.]
Description [The formula is represented by its index in the abTable]
SideEffects []
Definition at line 644 of file ltlAutomaton.c.
{
int result = 0;
Ctlsp_Formula_t *F, *notF;
LtlSet_t *UC;
int notF_ab_idx;
Ctlsp_FormulaType F_type;
F = tableau->abTable[index].F;
F_type = Ctlsp_FormulaReadType(F);
notF = tableau->abTable[index].notF;
notF_ab_idx = Ctlsp_FormulaReadABIndex(notF);
switch(tableau->algorithm) {
case Ltl2Aut_GPVW_c:
/* if 'u' is False, or (!u) exists in Current */
result = ( F_type == Ctlsp_FALSE_c ||
LtlSetGetElt(Current, notF_ab_idx) );
break;
case Ltl2Aut_GPVWplus_c:
/* if 'u' is False, or !(u) exists in Covered */
result = ( F_type == Ctlsp_FALSE_c ||
LtlSetGetElt(Covered, notF_ab_idx) );
break;
case Ltl2Aut_LTL2AUT_c:
case Ltl2Aut_WRING_c:
UC = LtlSetCopy(ToCover);
LtlSetOR(UC, ToCover, Current);
/* T iff (!u) \in SI(ToCover U Current) */
result = SI(tableau, notF_ab_idx, UC);
LtlSetFree(UC);
break;
}
#ifdef DEBUG_LTLMC
if (tableau->verbosity >2)
fprintf(vis_stdout, "...Contradiction=%d\n", result);
#endif
return result;
}
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:| static int HasToBeStored | ( | LtlTableau_t * | tableau, |
| int | index | ||
| ) | [static] |
AutomaticStart
Function********************************************************************
Synopsis [Return 1 iff the elementary formula need to be stored.]
Description [The formula is represented by its index in the abTable]
SideEffects []
Definition at line 602 of file ltlAutomaton.c.
{
int result = 1;
Ctlsp_Formula_t *F;
Ctlsp_FormulaType F_type;
F = tableau->abTable[index].F;
switch(tableau->algorithm) {
case Ltl2Aut_GPVW_c:
result = 1;
break;
case Ltl2Aut_GPVWplus_c:
/* T iff 'u' is an until formula or 'u' is the right hand of an until */
F_type = Ctlsp_FormulaReadType(F);
result = (F_type == Ctlsp_U_c || Ctlsp_FormulaReadRhs(F) == 1);
break;
case Ltl2Aut_LTL2AUT_c:
case Ltl2Aut_WRING_c:
result = 0;
break;
}
#ifdef DEBUG_LTLMC
if (tableau->verbosity >2)
fprintf(vis_stdout, "...HasToBeStored=%d\n", result);
#endif
return result;
}
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:| Ltl_Automaton_t* Ltl_AutomatonCreate | ( | void | ) |
AutomaticEnd Function********************************************************************
Synopsis [Allocate the automaton data structure.]
Description []
SideEffects []
SeeAlso []
Definition at line 76 of file ltlAutomaton.c.
{
Ltl_Automaton_t *aut = ALLOC(Ltl_Automaton_t, 1);
(void)memset((void *)aut, 0, sizeof(Ltl_Automaton_t));
aut->name = 0;
aut->SCC = (st_table *)0;
aut->G = g_alloc();
/* table of the initial states */
aut->Init = st_init_table(st_ptrcmp, st_ptrhash);
/* these states can be either in or outside the "FairSet" */
aut->dontcare = st_init_table(st_ptrcmp, st_ptrhash);
/* list of FairSets (each FairSet is a table of states) */
aut->Fair = lsCreate();
aut->node_idx = 1;
return aut;
}
 Here is the caller graph for this function:
Here is the caller graph for this function:| void Ltl_AutomatonFree | ( | gGeneric | g | ) |
Function********************************************************************
Synopsis [Free the automaton data structure.]
Description []
SideEffects []
SeeAlso []
Definition at line 107 of file ltlAutomaton.c.
{
st_table *tbl;
st_generator *stgen;
int i, n;
Ltl_Automaton_t *aut = (Ltl_Automaton_t *) g;
if (aut->name) FREE(aut->name);
g_free(aut->G, (void (*)(gGeneric))0, Ltl_AutomatonNodeFree,
(void (*)(gGeneric))0);
st_free_table(aut->Init);
st_free_table(aut->dontcare);
while (lsDelBegin(aut->Fair, &tbl) != LS_NOMORE) {
st_free_table(tbl);
}
lsDestroy(aut->Fair, (void (*)(lsGeneric)) NULL);
if (aut->labelTable) {
n = array_n(aut->labelTable);
for (i=0; i<n; i++)
Ctlsp_FormulaFree(array_fetch(Ctlsp_Formula_t *,
aut->labelTable, i));
array_free(aut->labelTable);
array_free(aut->labelTableNegate);
}
/* free the partition/quotient */
if (aut->SCC) {
/* for a Buechi automaton, this is a st_table of st_table of vertices;
* otherwise, this is a st_table of vertices */
if (aut->isQuotientGraph == 0) {
st_foreach_item(aut->SCC, stgen, &tbl, NIL(char *)) {
st_free_table(tbl);
}
}
st_free_table(aut->SCC);
}
if (aut->Q)
Ltl_AutomatonFree((gGeneric) aut->Q);
FREE(aut);
}
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:| Ltl_AutomatonNode_t* Ltl_AutomatonNodeCreate | ( | Ltl_Automaton_t * | aut | ) |
Function********************************************************************
Synopsis [Allocate the automaton node data structure.]
Description []
SideEffects []
SeeAlso []
Definition at line 166 of file ltlAutomaton.c.
{
Ltl_AutomatonNode_t *node = ALLOC(Ltl_AutomatonNode_t, 1);
(void)memset((void *)node, 0, sizeof(Ltl_AutomatonNode_t));
node->index = aut->node_idx++;
node->Labels = NIL(LtlSet_t);
node->CoverSet = NIL(LtlSet_t);
node->Class = (st_table *)0; /* used in Quotient graph */
return node;
}
 Here is the caller graph for this function:
Here is the caller graph for this function:| void Ltl_AutomatonNodeFree | ( | gGeneric | g | ) |
Function********************************************************************
Synopsis [Free the automaton node data structure.]
Description []
SideEffects []
SeeAlso []
Definition at line 191 of file ltlAutomaton.c.
{
Ltl_AutomatonNode_t *node = (Ltl_AutomatonNode_t *) g;
if (node->Labels)
LtlSetFree(node->Labels);
if (node->CoverSet)
LtlSetFree(node->CoverSet);
/* if (node->Class)
st_free_table(node->Class);*/
FREE(node);
}
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:| void Ltl_AutomatonNodePrint | ( | Ltl_Automaton_t * | aut, |
| Ltl_AutomatonNode_t * | node | ||
| ) |
Function********************************************************************
Synopsis [Print the automaton node.]
Description []
SideEffects []
SeeAlso []
Definition at line 216 of file ltlAutomaton.c.
{
st_generator *stgen;
vertex_t *vtx;
Ltl_AutomatonNode_t *state;
Ctlsp_Formula_t *F;
int first, i, n;
/* index (required) */
fprintf(vis_stdout, "n%d: ", node->index);
/* 1. cover (set of formulae) ? */
if (aut->tableau && node->CoverSet)
LtlSetPrint(aut->tableau, node->CoverSet);
/* 2. label ? */
if (node->Labels) {
fprintf(vis_stdout, " label: {");
first = 1; n = array_n(aut->labelTable);
for (i=0; i<n; i++) {
if (LtlSetGetElt(node->Labels, i)) {
if (!first) fprintf(vis_stdout, ",");
else first = 0;
F = array_fetch(Ctlsp_Formula_t *, aut->labelTable, i);
Ctlsp_FormulaPrint(vis_stdout, F);
}
}
fprintf(vis_stdout, "}");
}
/* 3. Class ? (for quotient graph node) */
if (node->Class) {
fprintf(vis_stdout, "scc{");
st_foreach_item(node->Class, stgen, &vtx, NIL(char *)) {
state = (Ltl_AutomatonNode_t *)vtx->user_data;
fprintf(vis_stdout, "n%d ", state->index);
}
fprintf(vis_stdout, "}");
}
fprintf(vis_stdout, "\n");
}
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:| void Ltl_AutomatonPrint | ( | Ltl_Automaton_t * | aut, |
| int | verbosity | ||
| ) |
Function********************************************************************
Synopsis [Print the automaton.]
Description []
SideEffects []
SeeAlso []
Definition at line 273 of file ltlAutomaton.c.
{
edge_t *edge;
vertex_t *vtx1, *vtx2;
Ltl_AutomatonNode_t *node, *node2;
lsGen gen;
lsGeneric data;
st_table *tbl;
st_generator *stgen;
int n_states = 0;
int n_trans = 0;
int n_fairsets = 0;
int n_init = 0;
int strength;
/* name ? */
if (verbosity)
fprintf(vis_stdout, "Automaton:\n");
if (verbosity > 1) {
fprintf(vis_stdout, "-----------------------------------------------\n");
if (aut->name)
fprintf(vis_stdout, "Name: %s \n", aut->name);
fprintf(vis_stdout, "-----------------------------------------------\n");
/* negation normal form ?*/
if(aut->tableau)
Ctlsp_FormulaPrint(vis_stdout, aut->tableau->F);
/* States & Labels */
fprintf(vis_stdout, "\nStates: \n");
foreach_vertex( aut->G, gen, vtx1) {
node = (Ltl_AutomatonNode_t *) vtx1->user_data;
Ltl_AutomatonNodePrint(aut, node);
}
/* Init States ? */
fprintf(vis_stdout, "Arcs: \n");
st_foreach_item(aut->Init, stgen, &vtx1, NIL(char *)) {
node = (Ltl_AutomatonNode_t *) vtx1->user_data;
fprintf(vis_stdout, "-> n%d\n", node->index);
}
/* Edges */
foreach_edge(aut->G, gen, edge) {
vtx1 = g_e_source(edge);
vtx2 = g_e_dest(edge);
node = (Ltl_AutomatonNode_t *) vtx1->user_data;
node2 = (Ltl_AutomatonNode_t *) vtx2->user_data;
if (node)
fprintf(vis_stdout, " n%d -> ", node->index);
if (node2)
fprintf(vis_stdout, "n%d\n", node2->index);
}
/* Sets of Fair Sets */
fprintf(vis_stdout, "Fair Sets: \n");
lsForEachItem (aut->Fair, gen, data) {
tbl = (st_table *) data;
fprintf(vis_stdout, "{ ");
st_foreach_item(tbl, stgen, &vtx1, NIL(char *)) {
node = (Ltl_AutomatonNode_t *) vtx1->user_data;
fprintf(vis_stdout, "n%d ", node->index);
}
fprintf(vis_stdout, " }\n");
}
#ifdef DEBUG_LTLMC
/* Dontcare states */
fprintf(vis_stdout, "Dontcare States: \n{");
if (aut->dontcare) {
st_foreach_item(aut->dontcare, stgen, &vtx1, NIL(char *)) {
node = (Ltl_AutomatonNode_t *) vtx1->user_data;
fprintf(vis_stdout, "n%d ", node->index);
}
}
fprintf(vis_stdout, " }\n");
#endif
fprintf(vis_stdout, "End\n");
}
/* Get the strength (2, 1, 0) */
n_states = lsLength(g_get_vertices(aut->G));
n_init = st_count(aut->Init);
n_trans = lsLength(g_get_edges(aut->G));
n_fairsets = lsLength(aut->Fair);
strength = Ltl_AutomatonGetStrength(aut);
if (verbosity)
fprintf(vis_stdout, "Stats: %d states, %d trans, %d fair sets, %d init states, %s\n", n_states, n_trans, n_fairsets, n_init, (strength==2)? "strong":((strength==1)?"weak":"terminal") );
}
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:| Ltl_Automaton_t* LtlAutomatonGeneration | ( | LtlTableau_t * | tableau | ) |
Function********************************************************************
Synopsis [Generate the Buechi automaton from the formula.]
Description [Before calling this function, 'tableau' should contains: 1) LTL Formula (NNF) and its negation in a DAG (or UniqueTable) 2) alpha-beta Table (tableau-rule expansion of each sub-formulae ) 3) Until formulae list.]
SideEffects [The returned automaton should be freed by the caller.]
SeeAlso []
Definition at line 392 of file ltlAutomaton.c.
{
LtlSet_t *toCover, *s, *r, *rprime; /* terms (set) */
lsList Cover; /* current list of terms (cover) */
lsList U = lsCreate(); /* a list of terms <to be processed>*/
lsList Q = lsCreate(); /* unique table for terms <processed> */
st_table *Set2Vtx = st_init_table(st_ptrcmp, st_ptrhash);
vertex_t *vtx1, *vtx2; /* vertex in graph, related to node */
Ltl_Automaton_t *A = Ltl_AutomatonCreate();
Ltl_AutomatonNode_t *node;
Ctlsp_Formula_t *F;
int i;
A->tableau = tableau;
/* Compute Cover( {F} ), the init states, and U */
toCover = AutomatonSetCreate(tableau, tableau->F);
Cover = AutomatonBuildCover(tableau, toCover);
while (lsDelBegin(Cover, &r) != LS_NOMORE) {
#ifdef DEBUG_LTLMC
if (tableau->verbosity >=2) {
fprintf(vis_stdout, "**** term: ");
LtlSetPrintIndex(tableau->abIndex, r);
fprintf(vis_stdout, "**** n%d added! \n", A->node_idx);
}
#endif
lsNewEnd(U, (lsGeneric) r, (lsHandle *) 0);
lsNewEnd(Q, (lsGeneric) r, (lsHandle *) 0);
/* Build the initial states of the Buechi automaton
* add a new node in G
*/
node = Ltl_AutomatonNodeCreate(A);
node->Labels = LtlSetToLabelSet(tableau, r);
node->CoverSet = LtlSetCopy(r);
vtx1 = g_add_vertex(A->G);
vtx1->user_data = (gGeneric) node;
/* add into A->Init */
st_insert(A->Init, vtx1, vtx1);
/* put this node to proper Fair sets */
AutomatonComputeFair(tableau, r, vtx1);
/* add into the (Set, Vtx) unique table */
st_insert(Set2Vtx, r, vtx1);
}
lsDestroy(Cover, (void (*)(lsGeneric))0);
/* Each time, remove one set 's' from the to-be-processed list 'U' */
while (lsDelBegin(U, &s) == LS_OK) {
/* Put all the next (state) formulae into toCover */
AutomatonAssignNext(tableau, toCover, s);
#ifdef DEBUG_LTLMC
if (tableau->verbosity >= 2) {
fprintf(vis_stdout, "\n** AssignNext Of:");
LtlSetPrintIndex(tableau->abIndex, s);
fprintf(vis_stdout, "** ==> ");
LtlSetPrintIndex(tableau->abIndex, toCover);
}
#endif
/* Build the cover for next state */
Cover = AutomatonBuildCover(tableau, toCover);
while (lsDelBegin(Cover, &r) == LS_OK) {
/* Get the existing identical copy of r from Q (if exist) */
rprime = LtlSetIsInList(r, Q);
#ifdef DEBUG_LTLMC
if (tableau->verbosity >=2 ) {
fprintf(vis_stdout, "** term: ");
LtlSetPrintIndex(tableau->abIndex, r);
}
#endif
/* If the next state exists, simply add the new edge; Otherwise,
create the next state, and add the new edge */
if (rprime) {
/* both s and r' are already in G */
st_lookup(Set2Vtx, rprime, &vtx1);
assert(vtx1 != NIL(vertex_t));
st_lookup(Set2Vtx, s, &vtx2);
assert(vtx2 != NIL(vertex_t));
/* add edge(s, r') */
g_add_edge(vtx2, vtx1);
LtlSetFree(r);
}else {
#ifdef DEBUG_LTLMC
if (tableau->verbosity >=2 ) {
fprintf(vis_stdout, "** n%d added!\n", A->node_idx);
}
#endif
/* add a new state in G */
node = Ltl_AutomatonNodeCreate(A);
node->Labels = LtlSetToLabelSet(tableau, r);
node->CoverSet = LtlSetCopy(r);
vtx1 = g_add_vertex(A->G);
vtx1->user_data = (gGeneric) node;
/* add edge(s, r) */
st_lookup(Set2Vtx, s, &vtx2);
assert(vtx2 != NIL(vertex_t));
g_add_edge(vtx2, vtx1);
/* put the new state to the proper Fair Sets */
AutomatonComputeFair(tableau, r, vtx1);
/* add r in the (Set, Vtx) unique table */
st_insert(Set2Vtx, r, vtx1);
lsNewEnd(Q, (lsGeneric) r, (lsHandle *) 0);
lsNewEnd(U, (lsGeneric) r, (lsHandle *) 0);
}
}
lsDestroy(Cover, (void (*)(lsGeneric))0);
}
/* Convert fair sets of the tableau into fair sets of the automaton:
* if there is an empty fairset, create an empty automaton and return;
* otherwise, keep going ...
*/
if (AutomatonCreateFairList(tableau, A) == 0) {
st_table *tbl;
while (lsDelBegin(A->Fair, &tbl) != LS_NOMORE) {
st_free_table(tbl);
}
g_free(A->G, (void (*)(gGeneric))0, Ltl_AutomatonNodeFree,
(void (*)(gGeneric))0);
A->G = g_alloc();
st_free_table(A->Init);
A->Init = st_init_table(st_ptrcmp, st_ptrhash);
}
/* Copy the lable table of the tableau into the automaton
* Note that the new one shares nothing with the one in the tableau
*/
A->labelTable = array_alloc(Ctlsp_Formula_t *, tableau->labelIndex);
for (i=0; i<tableau->labelIndex; i++) {
F = Ctlsp_LtlFormulaNegationNormalForm(tableau->labelTable[i]);
array_insert(Ctlsp_Formula_t *, A->labelTable, i, F);
}
A->labelTableNegate = array_dup(tableau->labelTableNegate);
/* Free all the sets in the list
* toCover/U should be empty sets, while Q contains all the processed set
*/
LtlSetFree(toCover);
lsDestroy(U, (void (*)(lsGeneric)) 0);
lsDestroy(Q, (void (*)(lsGeneric))LtlSetFree);
st_free_table(Set2Vtx);
#ifdef DEBUG_LTLMC
/* sanity check */
g_check(A->G);
#endif
return A;
}
 Here is the call graph for this function:
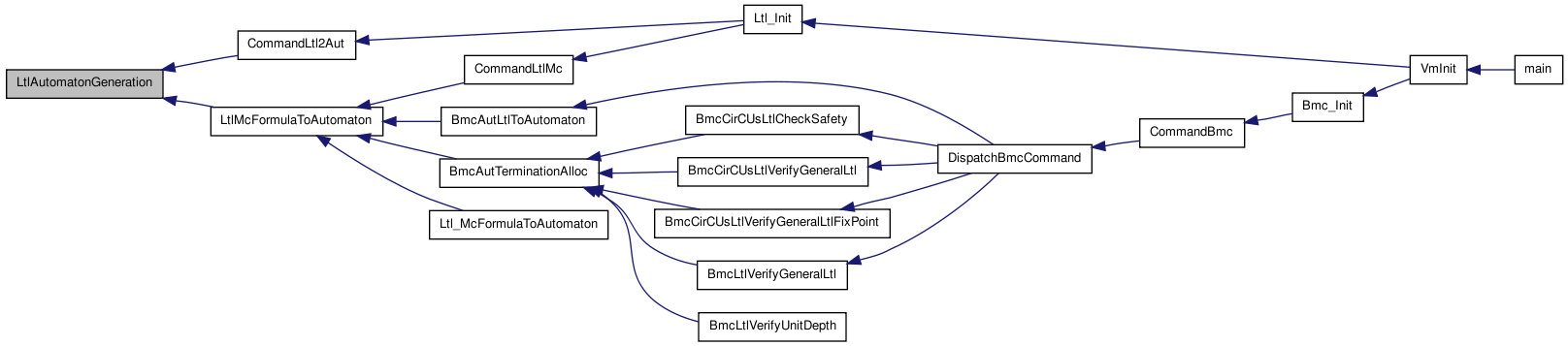
Here is the call graph for this function: Here is the caller graph for this function:
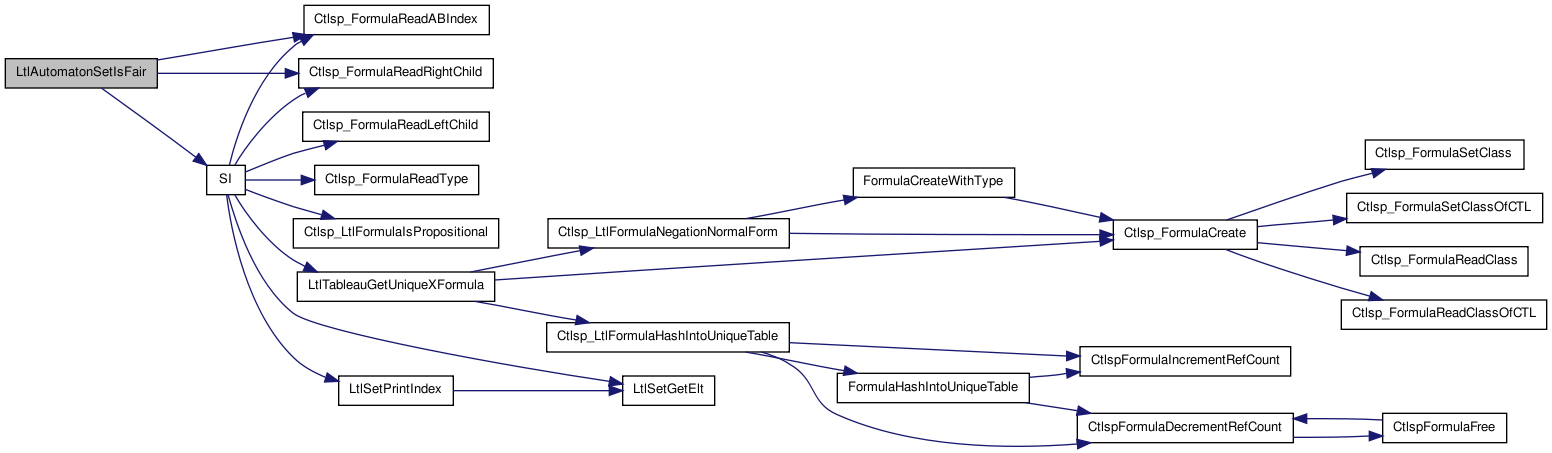
Here is the caller graph for this function:| int LtlAutomatonSetIsFair | ( | LtlTableau_t * | tableau, |
| LtlSet_t * | r | ||
| ) |
Function********************************************************************
Synopsis [Return 1 if the given set belongs to a fair set.]
Description [It is used in Boolean minimization. It might prevent over-simplification.]
SideEffects []
Definition at line 554 of file ltlAutomaton.c.
{
#if 0
st_table *uniqueTable = tableau->untilUniqueTable;
char *key, *value;
st_generator *gen;
int flag = 0;
#endif
/* this is the same as "Wring" */
return 0;
#if 0
st_foreach_item(uniqueTable, gen, &key, &value) {
Ctlsp_Formula_t *F = (Ctlsp_Formula_t *) key;
Ctlsp_Formula_t *right = Ctlsp_FormulaReadRightChild(F);
int F_ab_idx = Ctlsp_FormulaReadABIndex(F);
int right_ab_idx = Ctlsp_FormulaReadABIndex(right);
if ( SI(tableau, right_ab_idx, r) ||
!(SI(tableau, F_ab_idx, r)) ) {
/* set 'r' belongs to one fair set */
flag = 1;
st_free_gen(gen);
break;
}
}
return flag;
#endif
}
 Here is the call graph for this function:
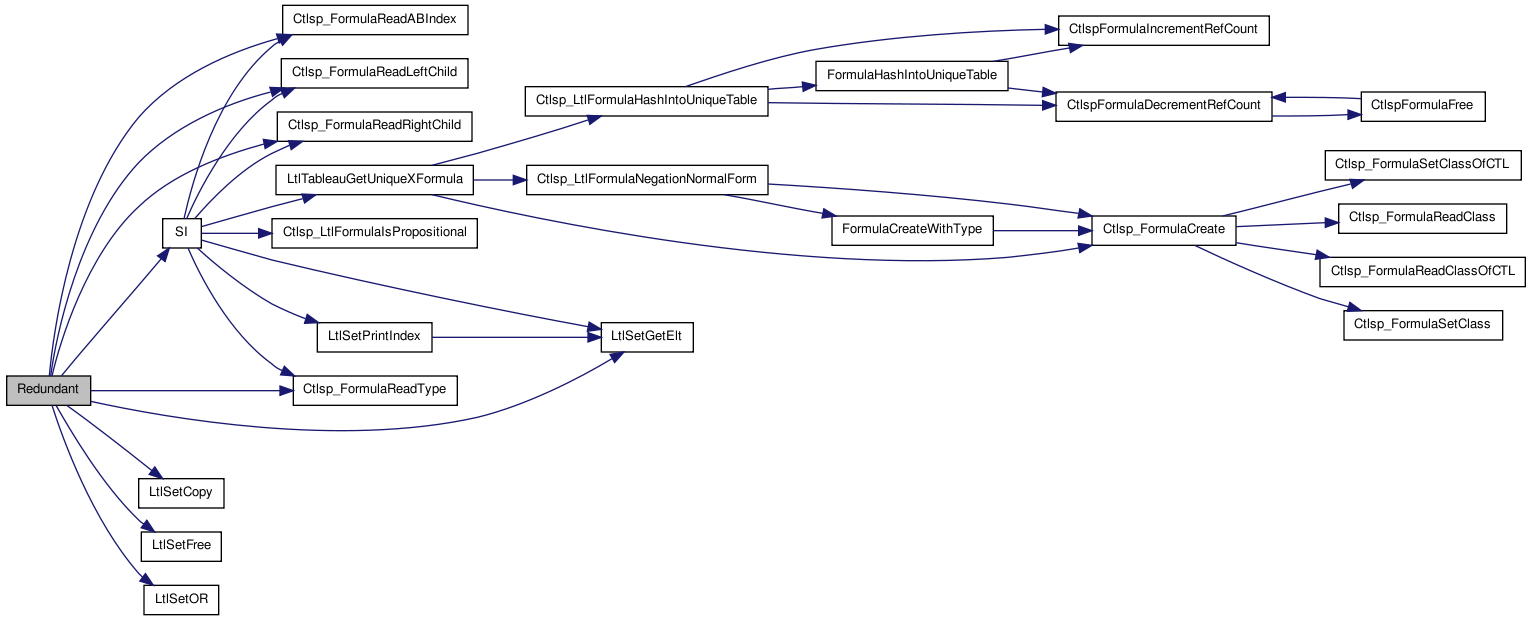
Here is the call graph for this function:| static int Redundant | ( | LtlTableau_t * | tableau, |
| int | index, | ||
| LtlSet_t * | ToCover, | ||
| LtlSet_t * | Current, | ||
| LtlSet_t * | Covered | ||
| ) | [static] |
Function********************************************************************
Synopsis [Return 1 iff the given formula is redundant.]
Description [The formula is represented by its index in the abTable]
SideEffects []
Definition at line 701 of file ltlAutomaton.c.
{
int result = 0;
Ctlsp_Formula_t *F;
LtlSet_t *UC = LtlSetCopy(ToCover);
int Fleft_ab_idx , Fright_ab_idx;
Ctlsp_FormulaType F_type;
LtlSetOR(UC, ToCover, Current);
F = tableau->abTable[index].F;
F_type = Ctlsp_FormulaReadType(F);
if (F_type == Ctlsp_U_c || F_type == Ctlsp_R_c) {
Fleft_ab_idx = Ctlsp_FormulaReadABIndex(Ctlsp_FormulaReadLeftChild(F));
Fright_ab_idx = Ctlsp_FormulaReadABIndex(Ctlsp_FormulaReadRightChild(F));
} else { /* to remove uninitialized variable warnings */
Fleft_ab_idx = 0;
Fright_ab_idx = 0;
}
switch(tableau->algorithm) {
case Ltl2Aut_GPVW_c:
result = 0;
break;
case Ltl2Aut_GPVWplus_c:
/* T iff 'u' is (n U v) and {v} is in (ToCover U Current),
* or 'u' is (n R v) and {n,v} is in (ToCover U Current)
*/
if (F_type == Ctlsp_U_c)
result = LtlSetGetElt(UC, Fright_ab_idx);
else if (F_type == Ctlsp_R_c)
result = ( LtlSetGetElt(UC, Fleft_ab_idx) &&
LtlSetGetElt(UC, Fright_ab_idx) );
else
result = 0;
break;
case Ltl2Aut_LTL2AUT_c:
case Ltl2Aut_WRING_c:
/* T iff the following two cases are both true:
* (1) 'u' is in SI(ToCover U Current)
* (2) if 'u' is (n U v), then 'v' is in (ToCover U Current)
*/
result = SI(tableau, index, UC);
if (result && F_type == Ctlsp_U_c) {
result = SI(tableau, Fright_ab_idx, UC);
}
break;
}
LtlSetFree(UC);
#ifdef DEBUG_LTLMC
if (tableau->verbosity >2)
fprintf(vis_stdout, "...Redundant=%d\n", result);
#endif
return result;
}
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:| static int SI | ( | LtlTableau_t * | tableau, |
| int | index, | ||
| LtlSet_t * | A | ||
| ) | [static] |
Function********************************************************************
Synopsis [Test if the given formula is synatically implied by the existing set (product term).]
Description [Return 1 if the formula is implied. The formula is represented by its index in the abTable]
SideEffects []
Definition at line 775 of file ltlAutomaton.c.
{
int result = 0;
Ctlsp_Formula_t *XF;
Ctlsp_Formula_t *F = tableau->abTable[index].F;
Ctlsp_FormulaType F_type = Ctlsp_FormulaReadType(F);
int Fleft_ab_idx, Fright_ab_idx;
if (tableau->algorithm == Ltl2Aut_GPVW_c ||
tableau->algorithm == Ltl2Aut_GPVWplus_c) {
result = LtlSetGetElt(A, index);
} else {
if (F_type == Ctlsp_AND_c || F_type == Ctlsp_OR_c ||
F_type == Ctlsp_U_c || F_type == Ctlsp_R_c) {
Fleft_ab_idx =
Ctlsp_FormulaReadABIndex(Ctlsp_FormulaReadLeftChild(F));
Fright_ab_idx =
Ctlsp_FormulaReadABIndex(Ctlsp_FormulaReadRightChild(F));
} else { /* to remove uninitialized variable warnings */
Fleft_ab_idx = 0;
Fright_ab_idx = 0;
}
switch(Ctlsp_FormulaReadType(F)) {
case Ctlsp_FALSE_c:
result = 0;
break;
case Ctlsp_TRUE_c:
result = 1;
break;
case Ctlsp_X_c:
case Ctlsp_NOT_c:
case Ctlsp_ID_c:
result = LtlSetGetElt(A, index);
break;
case Ctlsp_AND_c:
if (Ctlsp_LtlFormulaIsPropositional(F))
result = LtlSetGetElt(A, index);
else {
result = (SI(tableau, Fleft_ab_idx, A) &&
SI(tableau, Fright_ab_idx, A));
}
break;
case Ctlsp_OR_c:
if (Ctlsp_LtlFormulaIsPropositional(F))
result = LtlSetGetElt(A, index);
else {
result = (SI(tableau, Fleft_ab_idx, A) ||
SI(tableau, Fright_ab_idx, A));
}
break;
case Ctlsp_U_c:
XF = LtlTableauGetUniqueXFormula(tableau, F);
result = (SI(tableau, Fright_ab_idx, A) ||
(SI(tableau, Fleft_ab_idx, A) &&
LtlSetGetElt(A, Ctlsp_FormulaReadABIndex(XF))));
break;
case Ctlsp_R_c:
XF = LtlTableauGetUniqueXFormula(tableau, F);
result = SI(tableau, Fright_ab_idx, A) &&
(SI(tableau, Fleft_ab_idx, A) ||
LtlSetGetElt(A, Ctlsp_FormulaReadABIndex(XF)));
break;
default:
assert(0);
}
}
#ifdef DEBUG_LTLMC
if (tableau->verbosity > 3) {
fprintf(vis_stdout, "...SI( %d, ", index);
LtlSetPrintIndex(tableau->abIndex, A);
fprintf(vis_stdout, " )=%d\n", result);
}
#endif
return result;
}
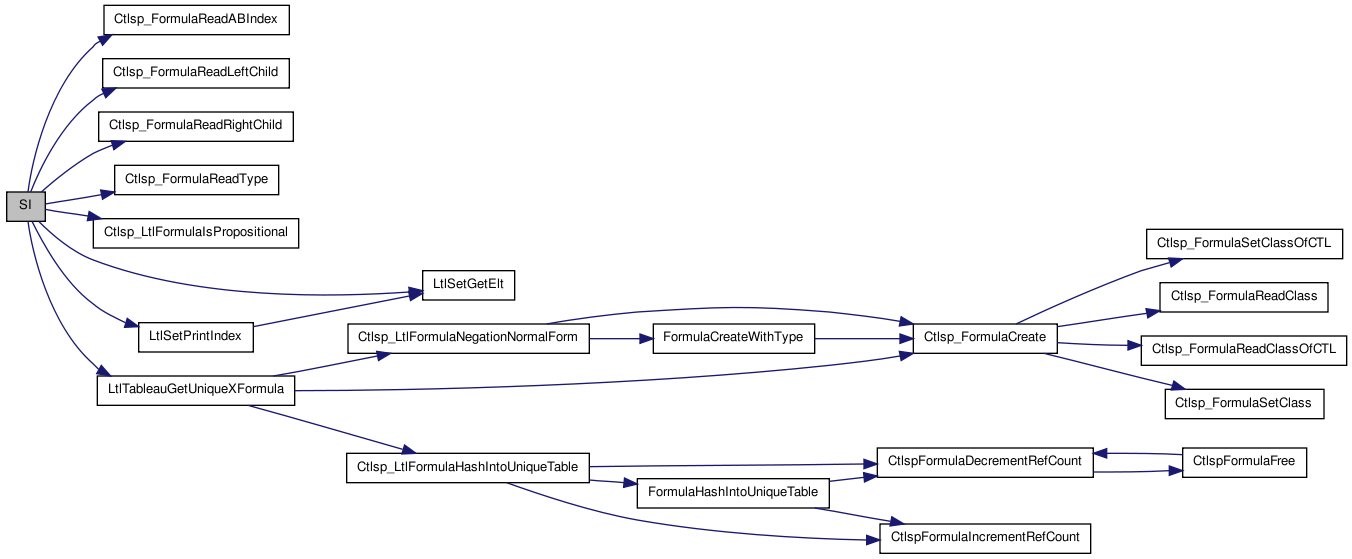
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:Variable Documentation
char rcsid [] UNUSED = "$Id: ltlAutomaton.c,v 1.34 2005/04/28 08:47:15 bli Exp $" [static] |
CFile***********************************************************************
FileName [ltlAutomaton.c]
PackageName [ltl]
Synopsis [Translate LTL formula to the Buechi Automaton.]
Author [Chao Wang<chao.wang@colorado.EDU>]
Copyright [This file was created at the University of Colorado at Boulder. The University of Colorado at Boulder makes no warranty about the suitability of this software for any purpose. It is presented on an AS IS basis.]
Definition at line 19 of file ltlAutomaton.c.