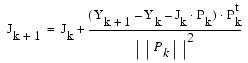Print version of this Book (PDF file)
Search Methods
Nine search methods are available within IC-CAP:
| • | Levenberg-Marquardt Search |
| • | Random Search |
| • | Hybrid (Random/LM) Search |
| • | Hybrid (Random/Quasi-Newton) Search |
| • | Sensitivity Analysis |
| • | Gradient Search |
| • | Quasi-Newton Search |
| • | Minimax (Gauss-Newton/Quasi-Newton) Search |
| • | Genetic Search |
For initial optimization, use Random search. As the optimization proceeds, move to a Gradient search to increase process speed.
Note
Levenberg-Marquardt Search
The Levenberg-Marquardt method uses a nonlinear, least-squares-fit (Levenberg-Marquardt) algorithm. This algorithm combines the steepest descent and Gauss-Newton methods.
The Levenberg-Marquardt method calculates the specified model parameters until the RMS error between measured and simulated data is minimized.
If the model is well-behaved and local minima are not a problem, use Levenberg-Marquardt Optimization.
Note
For example, assume the model parameters to be optimized are represented by the vector X:
The cost function to be minimized, F(X), is the sum of the squares of the difference between measured and simulated values of the specified output variable (such as, Id in the case of MOSFET).
The optimizer finds the vector X of the model parameters that minimizes F(X).
The Levenberg-Marquardt method is a minimization algorithm, requiring the first derivative of this function. This method combines the Steepest Descent and Gauss-Newton methods.
Steepest Descent Method
The Steepest Descent method is an iterative algorithm for finding Xk + 1 = Xk - a · Gk where G is the gradient of Fk and the scalar a 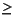 0 minimizes F ( Xk - a · Gk ). The algorithm searches along the negative gradient -Gk from the point Xk to a minimum point (Xk + 1) on the line.
0 minimizes F ( Xk - a · Gk ). The algorithm searches along the negative gradient -Gk from the point Xk to a minimum point (Xk + 1) on the line.
Gauss-Newton Method
Newton's method is based on the assumption that near the minimum point Xmin, the function F(x) can be approximated by a quadratic function. The truncated Taylor's vector series uses the following formula:
where H is the Hessian or second gradient of F. The above expression is minimized at ![]() therefore
therefore ![]() .
.
The Gauss-Newton method is a modified version of Newton which approximates the Hessian by 2 · Jt · J where J is the Jacobian or the first derivative of F and Jt is its transposed matrix.
Levenberg-Marquardt Method
This method generates a sequence of approximation to the minimum point by the formula:
- Xk + 1 = Xk + Pk
- where
- Pk = -(Jt · J + Lambda · I)-1 · Jt · F(x)
- I is the identity matrix.
- Lambda is the Marquardt parameter, which is the sequence of non-negative real constants.
- where
As Lambda becomes very large relative to the norm Jt · J, Pk tends toward the direction of steepest descent. When Lambda is very small, the Gauss-Newton solution is obtained.
For a bad initial estimate, Lambda is chosen large. The algorithm then behaves like the steepest descent, giving large improvements in the minimization of the objective function F(x) to guarantee convergence.
Within the iteration, Lambda is increased until a reduction in F(x) is achieved. Between iterations, Lambda is reduced successively so that as the minimum is reached, Pk tends to move closer to the Gauss-Newton direction. This ensures that the overall algorithm has second order convergence near the minimum.
Jacobian Calculation
The Jacobian is numerically calculated using the forward difference approximation:
This requires n+1 function evaluations for each iteration point Xk. To reduce the number of function evaluations, Broyden's rank one correction method approximates the Jacobian:
IC-CAP calculates the actual Jacobian after every n iterations
(n = the number of parameters) or when the Lambda is increased.
Random Search
The Random, Random (Gucker), and Random Minimax optimizers arrive at new parameter values by using a random-number generator to choose random values within a range until the specified RMS error value is obtained.
This random process can be slower compared to the optimizers using complex gradient search methods.
Note
Random optimization is useful for avoiding local minima, before or after a Levenberg-Marquardt optimization. It can be used before Levenberg-Marquardt optimization to reduce the error to an acceptable starting point for Levenberg-Marquardt, or after to make sure that the global minimum has been reached.
Optimization with random search method is a trial and error process. Starting from an initial set of parameter values for which the error function is known, a new set of values is obtained by perturbing each of the initial values, and the error function is re-evaluated.
For optimization with random search method, a trial consists of two error function evaluations. A trial is completed by reversing the algebraic sign of each parameter value perturbation and re-evaluating the error function. These two values, corresponding to positive and negative perturbations, are compared to the value at the initial point.
If either value is less than the initial value, then the set of parameter values for which the error function has its least value becomes the initial point for the next trial. If neither value is less than the initial value, then the initial point remains the same for the next trial.
Hybrid (Random/LM) Search
The Hybrid (Random/LM) search is a combination of the Random and Levenberg-Marquardt methods. At each random jump, the Levenberg-Marquardt optimizer is called and the RMS error is evaluated.
Hybrid (Random/LM) optimization takes advantage of the speed of Levenberg-Marquardt while using random jumps to avoid local minima.
If local minima present a problem, consider using Hybrid (Random/LM) optimization.
Note
Hybrid (Random/Quasi-Newton) Search
The Hybrid (Random/Quasi-Newton) optimizer combines the Random and quasi-Newton method. It offers a compromise between the ability to find a minimum quickly, using the fewest possible parameter analyses (the strength of quasi-Newton optimization) and the possibility to find the global cost minimum in the presence of many local minima (the strength of Random optimization).
When Hybrid (Random/Quasi-Newton) optimization is selected, the process begins with a quasi-Newton search, quickly finding the nearest local minimum. When the gradient approaches zero, it is near a minimum and can do little to decrease the cost function. The system then uses a random search technique to generate a new initial guess. Another quasi-Newton search is then performed, starting at this initial guess.
This process continues until the optimizer can no longer improve the performance of the model, or it reaches the specified maximum number of iterations.
Hybrid (Random/Quasi-Newton) optimization is an excellent choice if time is available for relatively long analyses.
Note
In summary, the Hybrid (Random/Quasi-Newton) optimizer:
| • | uses gradient information during the optimization, and |
| • | is useful for finding a local, as well as the global, minimum. |
Sensitivity Analysis
In sensitivity analysis mode, the partial derivatives of the data with respect to each parameter are printed. In addition, the partial derivatives at each data point are stored as transform data and can be viewed graphically. To gain insight into the sensitivities involved in a particular optimization, sensitivity analysis should be selected.
Gradient Search
The optimizers using gradient search method (Gradient and Gradient Minimax optimizers in Table 22) find the gradient of the network's error function. These optimizers usually progress more quickly to a point where the error function is minimized, though it is possible for them to terminate in a local minimum.
The optimizers find the gradient of the error function (i.e., the direction to move a set of parameter values in order to reduce the error function). Once the direction is determined, the set of parameter values is moved in that direction until the error function is minimized and the gradient is re-evaluated. This cycle equals one gradient optimizer iteration.
A single iteration usually includes many function evaluations. Therefore, a gradient search method iteration takes much longer than a random search method trial.
Note
Quasi-Newton Search
The optimizers using Quasi-Newton search method (Quasi-Newton and Least Pth optimizers in Table 22) use second-order derivatives of the error function and the gradient to find a descending direction.
The optimization routine using Quasi-Newton search method estimates the second-order derivatives using the Davidson-Fletcher-Powell (DFP) formula or its complement. Appropriately combined with the gradient, this information is used to find a direction and an inexact line-search is conducted.
The optimization terminates when the gradient vanishes, the change ratio in the variables is small (less than 1.0e-5), or the number of specified iterations is reached.
An iteration in the optimizers using Quasi-Newton search methods consists of many function evaluations, and requires more time than a random search method trial.
Note
Minimax (Gauss-Newton/Quasi-Newton) Search
The Minimax optimizer consists of two stages. In the first stage of the algorithm, the optimizer solves a minimax problem using a linear programming technique. In doing so, the status and potential of each individual error function component are analyzed. Its contribution to the minimax problem is mathematically assessed and taken into account during optimization.
In the second stage, the optimizer works with a Quasi-Newton method using approximate second-order derivatives. Such extra effort becomes necessary for an accurate and efficient solution to certain ill-conditioned problems (i.e., singular problems).
The Minimax optimizer terminates when responses become optimally equal-ripple, the relative change in the variables is less than 0.05 percent, or when the user-defined termination conditions are met (number of iterations, number of evaluations).
Genetic Search
Genetic algorithms (GA's) provide another direct search optimization method. The basis of the procedure is a set of trial parameter sets, sometimes called chromosomes, which are allowed to evolve towards a set that gives progressively better performance.
The key to the genetic optimization is the strategy of change, sometimes likened to survival of the fittest. Based on the idea that with each change in the parameter population, i.e., each generation of parameters, the performance given by the parameter population improves.
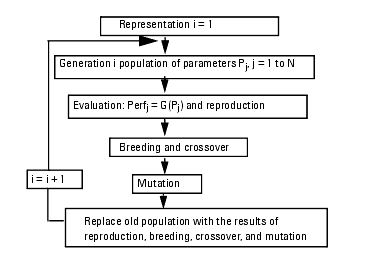
This performance evolution is achieved using a five-step process including (1) representation, (2) evaluation, (3) reproduction, (4) breeding and crossover, and (5) mutation.
| 1 | Representation: Genetic algorithms require the input parameter set to be represented as a string of digits. It is straightforward to map each parameter onto the interval 0 to 1, for instance, and then have each of the n parameters occupy a position in the string of n bounded numbers. The algorithm then manipulates and optimizes this string of numbers as a whole. An individual string of parameters is called an element within the population of parameter strings. |
| 2 | Evaluation: Each generation of parameters begins with a performance evaluation of each string in the population. Usually this involves determining the performance G(P) for each representation of P in the population. Each element is then graded as to how well it performed, often using an error function, known as the fitness function. |
| 3 | Reproduction: Some of the generation members are reproduced and added to the next generation population. The number of copies depends on the performance evaluation. The elements that perform well are copied several times, and those with poor performance are not copied at all. The copies, or offspring, comprise the next generation. Elements that are not copied are not represented in the next generation. |
- The number of elements in each generation is constant.
- There are several suggested methods of evaluation and reproduction, including ratioing, where the number of copies is directly related to the element's performance, and ranking where the performances are ranked, with the top performers being copied more times than the lower ranked performers.
- There are several suggested methods of evaluation and reproduction, including ratioing, where the number of copies is directly related to the element's performance, and ranking where the performances are ranked, with the top performers being copied more times than the lower ranked performers.
| 4 | Breeding and crossover: The previous step, reproduction, produced a population of strings where each evaluated well. Breeding then combines parts of two strings to form two different and new strings. In this way good representations are mixed with poorer representations, with the result eventually being evaluated in the next generation of the algorithm. |
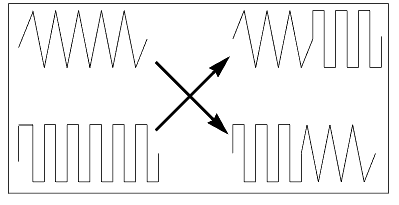
- There are many methods for breeding; the most common is crossover. Crossover typically takes two elements, splits them at a random location in the string, and swaps the two parts to create two new strings (see the following figure). This provides a controlled statistical exploration of the performance space.
Figure 23 Breeding and Crossover in the Simple Genetic Algorithm
| 5 | Mutation: The last step in creating a new generation of elements is the random changing of parameters in some of the surviving strings. This comprises a completely random search of the performance space, and can be viewed as the injection of information into the surviving population. |
The following figure presents a completed flow diagram of the genetic algorithm. The application of these techniques requires many tuning parameters that are not available with yield optimization.
Genetic optimization techniques will prove useful for many complex optimization problems, including discrete value and toleran
Genetic optimization will prove useful for many complex optimization problems, including discrete value and tolerance optimization.
Note
ce optimization.
Figure 24 Random-Search Optimization Using a Genetic Algorithm