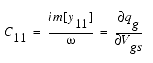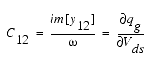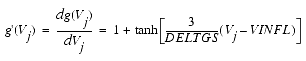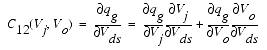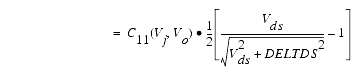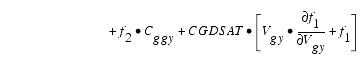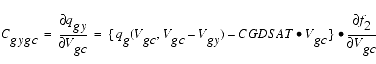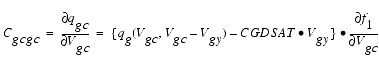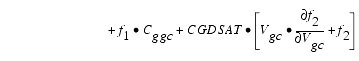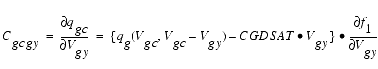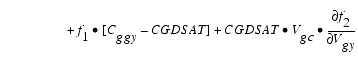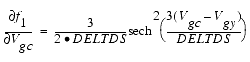Gate Charge Model

The Agilent EEHEMT1 gate charge model was developed through careful examination of extracted device capacitances over bias. The model consists of simple closed form charge expressions whose derivatives fit observed bias dependencies in capacitance data. This capacitance data can be obtained directly from measured Y-parameter data:

The capacitance data is remarkably self-consistent. In other words, a single q_g function's derivatives will fit both C₁₁ data and C₁₂ data. The Agilent EEHEMT1 gate charge expression is:

where

This expression is valid for both positive and negative V_ds. Symmetry is forced through the following smoothing functions proposed by Statz [4]:

Differentiating the gate charge expression wrt V_gs yields the following expression for the gate capacitance C₁₁:

where

The gate transcapacitance C₁₂ is defined as:

The Agilent EEHEMT1 topology requires that the gate charge be subdivided between the respective charge sources q_gc and q_gy. Although simulation could be performed directly from the nodal gate charge q_g, division of the charge into branches permits the inclusion of the resistances RIS and RID that model charging delay between the depletion region and the channel. Agilent EEHEMT1 assumes the following form for the gate-drain charge in saturation:

which gives rise to a constant gate-drain capacitance in saturation.

The gate-source charge q_gc can now be obtained by subtracting the latter from the gate charge equation.   Smoothing functions can then be applied to these expressions in saturation in order to extend the model's applicable bias range to all V_ds values. These smoothing functions force symmetry on the q_gy and q_gc charges such that

at V_gc = V_gy. Under large negative V_ds (saturation at the source end of the device), q_gy and q_gc swap roles, i.e:

The following continuous charge equations satisfy these constraints and are specified in terms of the gate charge:

where f₁ and f₂ are smoothing functions defined by

and

The capacitances associated with these branch charge sources can be obtained through differentiation of the q_gc and q_gy equations and by application of the chain rule to the capacitances C₁₁ and C₁₂.     The gate charge derivatives re-formulated in terms of V_gc and V_gy are:

The branch charge derivatives are:

where

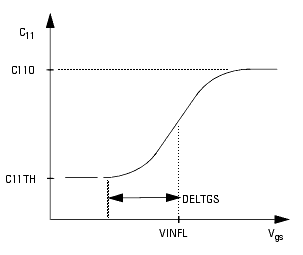
When V_ds=VDSO and VDSO>>DELTDS, the gate capacitance C₁₁ reduces to a single voltage dependency in V_gs. Similar to the I_ds model, the majority of the important gate charge parameters can then be estimated from a single trace of a plot. In this case, the plot of interest is C₁₁-V_gs at V_ds = VDSO. The parameter definitions are illustrated in the following figure.

The parameter DELTDS models the gate capacitance transition from the linear region of the device into saturation. LAMBDA models the slope of the C₁₁-V_ds characteristic in saturation. C12SAT is used to fit the gate transcapacitance (C₁₂) in saturation.

Figure 24 Agilent EEHEMT1 C₁₁-V_gs Parameters