src/base/abci/abcResub.c File Reference

#include "abc.h"
#include "dec.h"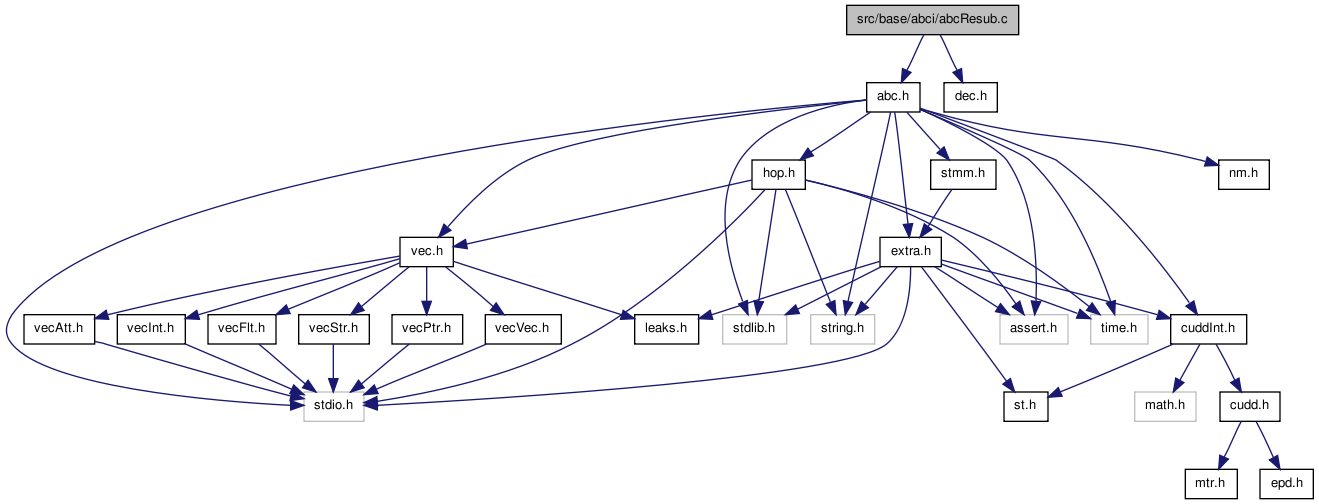
Include dependency graph for abcResub.c:

Go to the source code of this file.

Data Structures

struct  Abc_ManRes_t_

Defines

#define ABC_RS_DIV1_MAX   150
#define ABC_RS_DIV2_MAX   500

Typedefs

typedef struct Abc_ManRes_t_ Abc_ManRes_t

Functions

static Abc_ManRes_t * Abc_ManResubStart (int nLeavesMax, int nDivsMax)
static void Abc_ManResubStop (Abc_ManRes_t *p)
static Dec_Graph_t * Abc_ManResubEval (Abc_ManRes_t *p, Abc_Obj_t *pRoot, Vec_Ptr_t *vLeaves, int nSteps, bool fUpdateLevel, int fVerbose)
static void Abc_ManResubCleanup (Abc_ManRes_t *p)
static void Abc_ManResubPrint (Abc_ManRes_t *p)
static int Abc_ManResubCollectDivs (Abc_ManRes_t *p, Abc_Obj_t *pRoot, Vec_Ptr_t *vLeaves, int Required)
static void Abc_ManResubSimulate (Vec_Ptr_t *vDivs, int nLeaves, Vec_Ptr_t *vSims, int nLeavesMax, int nWords)
static void Abc_ManResubPrintDivs (Abc_ManRes_t *p, Abc_Obj_t *pRoot, Vec_Ptr_t *vLeaves)
static void Abc_ManResubDivsS (Abc_ManRes_t *p, int Required)
static void Abc_ManResubDivsD (Abc_ManRes_t *p, int Required)
static Dec_Graph_t * Abc_ManResubQuit (Abc_ManRes_t *p)
static Dec_Graph_t * Abc_ManResubDivs0 (Abc_ManRes_t *p)
static Dec_Graph_t * Abc_ManResubDivs1 (Abc_ManRes_t *p, int Required)
static Dec_Graph_t * Abc_ManResubDivs12 (Abc_ManRes_t *p, int Required)
static Dec_Graph_t * Abc_ManResubDivs2 (Abc_ManRes_t *p, int Required)
static Dec_Graph_t * Abc_ManResubDivs3 (Abc_ManRes_t *p, int Required)
static Vec_Ptr_t * Abc_CutFactorLarge (Abc_Obj_t *pNode, int nLeavesMax)
static int Abc_CutVolumeCheck (Abc_Obj_t *pNode, Vec_Ptr_t *vLeaves)
void * Abc_NtkDontCareAlloc (int nVarsMax, int nLevels, int fVerbose, int fVeryVerbose)
void Abc_NtkDontCareClear (void *p)
void Abc_NtkDontCareFree (void *p)
int Abc_NtkDontCareCompute (void *p, Abc_Obj_t *pNode, Vec_Ptr_t *vLeaves, unsigned *puTruth)
int Abc_NtkResubstitute (Abc_Ntk_t *pNtk, int nCutMax, int nStepsMax, int nLevelsOdc, bool fUpdateLevel, bool fVerbose, bool fVeryVerbose)
void Abc_ManResubCollectDivs_rec (Abc_Obj_t *pNode, Vec_Ptr_t *vInternal)
Dec_Graph_t * Abc_ManResubQuit0 (Abc_Obj_t *pRoot, Abc_Obj_t *pObj)
Dec_Graph_t * Abc_ManResubQuit1 (Abc_Obj_t *pRoot, Abc_Obj_t *pObj0, Abc_Obj_t *pObj1, int fOrGate)
Dec_Graph_t * Abc_ManResubQuit21 (Abc_Obj_t *pRoot, Abc_Obj_t *pObj0, Abc_Obj_t *pObj1, Abc_Obj_t *pObj2, int fOrGate)
Dec_Graph_t * Abc_ManResubQuit2 (Abc_Obj_t *pRoot, Abc_Obj_t *pObj0, Abc_Obj_t *pObj1, Abc_Obj_t *pObj2, int fOrGate)
Dec_Graph_t * Abc_ManResubQuit3 (Abc_Obj_t *pRoot, Abc_Obj_t *pObj0, Abc_Obj_t *pObj1, Abc_Obj_t *pObj2, Abc_Obj_t *pObj3, int fOrGate)
int Abc_CutVolumeCheck_rec (Abc_Obj_t *pObj)
void Abc_CutFactor_rec (Abc_Obj_t *pObj, Vec_Ptr_t *vLeaves)
Vec_Ptr_t * Abc_CutFactor (Abc_Obj_t *pNode)

Variables

int s_ResubTime

Define Documentation

#define ABC_RS_DIV1_MAX   150

CFile****************************************************************

FileName [abcResub.c]

SystemName [ABC: Logic synthesis and verification system.]

PackageName [Network and node package.]

Synopsis [Resubstitution manager.]

Author [Alan Mishchenko]

Affiliation [UC Berkeley]

Date [Ver. 1.0. Started - June 20, 2005.]

Revision [

Id
abcResub.c,v 1.00 2005/06/20 00:00:00 alanmi Exp

] DECLARATIONS ///

Definition at line 28 of file abcResub.c.

#define ABC_RS_DIV2_MAX   500

Definition at line 29 of file abcResub.c.

Typedef Documentation

typedef struct Abc_ManRes_t_ Abc_ManRes_t

Definition at line 31 of file abcResub.c.

Function Documentation

Vec_Ptr_t* Abc_CutFactor ( Abc_Obj_t *  pNode  ) 

Function*************************************************************

Synopsis [Computes the factor cut of the node.]

Description [Factor-cut is the cut at a node in terms of factor-nodes. Factor-nodes are roots of the node trees (MUXes/EXORs are counted as single nodes). Factor-cut is unique for the given node.]

SideEffects []

SeeAlso []

Definition at line 1820 of file abcResub.c.

01821 {
01822     Vec_Ptr_t * vLeaves;
01823     Abc_Obj_t * pObj;
01824     int i;
01825     assert( !Abc_ObjIsCi(pNode) );
01826     vLeaves  = Vec_PtrAlloc( 10 );
01827     Abc_CutFactor_rec( Abc_ObjFanin0(pNode), vLeaves );
01828     Abc_CutFactor_rec( Abc_ObjFanin1(pNode), vLeaves );
01829     Vec_PtrForEachEntry( vLeaves, pObj, i )
01830         pObj->fMarkA = 0;
01831     return vLeaves;
01832 }

void Abc_CutFactor_rec ( Abc_Obj_t *  pObj,
Vec_Ptr_t *  vLeaves 
)

Function*************************************************************

Synopsis [Computes the factor cut of the node.]

Description []

SideEffects []

SeeAlso []

Definition at line 1793 of file abcResub.c.

01794 {
01795     if ( pObj->fMarkA )
01796         return;
01797     if ( Abc_ObjIsCi(pObj) || (Abc_ObjFanoutNum(pObj) > 1 && !Abc_NodeIsMuxControlType(pObj)) )
01798     {
01799         Vec_PtrPush( vLeaves, pObj );
01800         pObj->fMarkA = 1;
01801         return;
01802     }
01803     Abc_CutFactor_rec( Abc_ObjFanin0(pObj), vLeaves );
01804     Abc_CutFactor_rec( Abc_ObjFanin1(pObj), vLeaves );
01805 }

Vec_Ptr_t * Abc_CutFactorLarge ( Abc_Obj_t *  pNode,
int  nLeavesMax 
) [static]

Function*************************************************************

Synopsis [Cut computation.]

Description [This cut computation works as follows: It starts with the factor cut at the node. If the factor-cut is large, quit. It supports the set of leaves of the cut under construction and labels all nodes in the cut under construction, including the leaves. It computes the factor-cuts of the leaves and checks if it is easible to add any of them. If it is, it randomly chooses one feasible and continues.]

SideEffects []

SeeAlso []

Definition at line 1850 of file abcResub.c.

01851 {
01852     Vec_Ptr_t * vLeaves, * vFactors, * vFact, * vNext;
01853     Vec_Int_t * vFeasible;
01854     Abc_Obj_t * pLeaf, * pTemp;
01855     int i, k, Counter, RandLeaf;
01856     int BestCut, BestShare;
01857     assert( Abc_ObjIsNode(pNode) );
01858     // get one factor-cut
01859     vLeaves = Abc_CutFactor( pNode );
01860     if ( Vec_PtrSize(vLeaves) > nLeavesMax )
01861     {
01862         Vec_PtrFree(vLeaves);
01863         return NULL;
01864     }
01865     if ( Vec_PtrSize(vLeaves) == nLeavesMax )
01866         return vLeaves;
01867     // initialize the factor cuts for the leaves
01868     vFactors = Vec_PtrAlloc( nLeavesMax );
01869     Abc_NtkIncrementTravId( pNode->pNtk );
01870     Vec_PtrForEachEntry( vLeaves, pLeaf, i )
01871     {
01872         Abc_NodeSetTravIdCurrent( pLeaf ); 
01873         if ( Abc_ObjIsCi(pLeaf) )
01874             Vec_PtrPush( vFactors, NULL );
01875         else
01876             Vec_PtrPush( vFactors, Abc_CutFactor(pLeaf) );
01877     }
01878     // construct larger factor cuts
01879     vFeasible = Vec_IntAlloc( nLeavesMax );
01880     while ( 1 )
01881     {
01882         BestCut = -1;
01883         // find the next feasible cut to add
01884         Vec_IntClear( vFeasible );
01885         Vec_PtrForEachEntry( vFactors, vFact, i )
01886         {
01887             if ( vFact == NULL )
01888                 continue;
01889             // count the number of unmarked leaves of this factor cut
01890             Counter = 0;
01891             Vec_PtrForEachEntry( vFact, pTemp, k )
01892                 Counter += !Abc_NodeIsTravIdCurrent(pTemp);
01893             // if the number of new leaves is smaller than the diff, it is feasible
01894             if ( Counter <= nLeavesMax - Vec_PtrSize(vLeaves) + 1 )
01895             {
01896                 Vec_IntPush( vFeasible, i );
01897                 if ( BestCut == -1 || BestShare < Vec_PtrSize(vFact) - Counter )
01898                     BestCut = i, BestShare = Vec_PtrSize(vFact) - Counter;
01899             }
01900         }
01901         // quit if there is no feasible factor cuts
01902         if ( Vec_IntSize(vFeasible) == 0 )
01903             break;
01904         // randomly choose one leaf and get its factor cut
01905 //        RandLeaf = Vec_IntEntry( vFeasible, rand() % Vec_IntSize(vFeasible) );
01906         // choose the cut that has most sharing with the other cuts
01907         RandLeaf = BestCut;
01908 
01909         pLeaf = Vec_PtrEntry( vLeaves, RandLeaf );
01910         vNext = Vec_PtrEntry( vFactors, RandLeaf );
01911         // unmark this leaf
01912         Abc_NodeSetTravIdPrevious( pLeaf ); 
01913         // remove this cut from the leaves and factor cuts
01914         for ( i = RandLeaf; i < Vec_PtrSize(vLeaves)-1; i++ )
01915         {
01916             Vec_PtrWriteEntry( vLeaves,  i, Vec_PtrEntry(vLeaves, i+1) );
01917             Vec_PtrWriteEntry( vFactors, i, Vec_PtrEntry(vFactors,i+1) );
01918         }
01919         Vec_PtrShrink( vLeaves,  Vec_PtrSize(vLeaves) -1 );
01920         Vec_PtrShrink( vFactors, Vec_PtrSize(vFactors)-1 );
01921         // add new leaves, compute their factor cuts
01922         Vec_PtrForEachEntry( vNext, pLeaf, i )
01923         {
01924             if ( Abc_NodeIsTravIdCurrent(pLeaf) )
01925                 continue;
01926             Abc_NodeSetTravIdCurrent( pLeaf ); 
01927             Vec_PtrPush( vLeaves, pLeaf );
01928             if ( Abc_ObjIsCi(pLeaf) )
01929                 Vec_PtrPush( vFactors, NULL );
01930             else
01931                 Vec_PtrPush( vFactors, Abc_CutFactor(pLeaf) );
01932         }
01933         Vec_PtrFree( vNext );
01934         assert( Vec_PtrSize(vLeaves) <= nLeavesMax );
01935         if ( Vec_PtrSize(vLeaves) == nLeavesMax )
01936             break;
01937     }
01938 
01939     // remove temporary storage
01940     Vec_PtrForEachEntry( vFactors, vFact, i )
01941         if ( vFact ) Vec_PtrFree( vFact );
01942     Vec_PtrFree( vFactors );
01943     Vec_IntFree( vFeasible );
01944     return vLeaves;
01945 }

int Abc_CutVolumeCheck ( Abc_Obj_t *  pNode,
Vec_Ptr_t *  vLeaves 
) [static]

Function*************************************************************

Synopsis [Computes the volume and checks if the cut is feasible.]

Description []

SideEffects []

SeeAlso []

Definition at line 1770 of file abcResub.c.

01771 {
01772     Abc_Obj_t * pObj;
01773     int i;
01774     // mark the leaves
01775     Abc_NtkIncrementTravId( pNode->pNtk );
01776     Vec_PtrForEachEntry( vLeaves, pObj, i )
01777         Abc_NodeSetTravIdCurrent( pObj ); 
01778     // traverse the nodes starting from the given one and count them
01779     return Abc_CutVolumeCheck_rec( pNode );
01780 }

int Abc_CutVolumeCheck_rec ( Abc_Obj_t *  pObj  ) 

Function*************************************************************

Synopsis [Computes the volume and checks if the cut is feasible.]

Description []

SideEffects []

SeeAlso []

Definition at line 1745 of file abcResub.c.

01746 {
01747     // quit if the node is visited (or if it is a leaf)
01748     if ( Abc_NodeIsTravIdCurrent(pObj) )
01749         return 0;
01750     Abc_NodeSetTravIdCurrent(pObj);
01751     // report the error
01752     if ( Abc_ObjIsCi(pObj) )
01753         printf( "Abc_CutVolumeCheck() ERROR: The set of nodes is not a cut!\n" );
01754     // count the number of nodes in the leaves
01755     return 1 + Abc_CutVolumeCheck_rec( Abc_ObjFanin0(pObj) ) +
01756         Abc_CutVolumeCheck_rec( Abc_ObjFanin1(pObj) );
01757 }

void Abc_ManResubCleanup ( Abc_ManRes_t *  p  )  [static]

Function*************************************************************

Synopsis []

Description []

SideEffects []

SeeAlso []

Definition at line 1597 of file abcResub.c.

01598 {
01599     Abc_Obj_t * pObj;
01600     int i;
01601     Vec_PtrForEachEntry( p->vDivs, pObj, i )
01602         pObj->pData = NULL;
01603     Vec_PtrClear( p->vDivs );
01604     p->pRoot = NULL;
01605 }

int Abc_ManResubCollectDivs ( Abc_ManRes_t *  p,
Abc_Obj_t *  pRoot,
Vec_Ptr_t *  vLeaves,
int  Required 
) [static]

Function*************************************************************

Synopsis []

Description []

SideEffects []

SeeAlso []

Definition at line 433 of file abcResub.c.

00434 {
00435     Abc_Obj_t * pNode, * pFanout;
00436     int i, k, Limit, Counter;
00437 
00438     Vec_PtrClear( p->vDivs1UP );
00439     Vec_PtrClear( p->vDivs1UN );
00440     Vec_PtrClear( p->vDivs1B );
00441 
00442     // add the leaves of the cuts to the divisors
00443     Vec_PtrClear( p->vDivs );
00444     Abc_NtkIncrementTravId( pRoot->pNtk );
00445     Vec_PtrForEachEntry( vLeaves, pNode, i )
00446     {
00447         Vec_PtrPush( p->vDivs, pNode );
00448         Abc_NodeSetTravIdCurrent( pNode );        
00449     }
00450 
00451     // mark nodes in the MFFC
00452     Vec_PtrForEachEntry( p->vTemp, pNode, i )
00453         pNode->fMarkA = 1;
00454     // collect the cone (without MFFC)
00455     Abc_ManResubCollectDivs_rec( pRoot, p->vDivs );
00456     // unmark the current MFFC
00457     Vec_PtrForEachEntry( p->vTemp, pNode, i )
00458         pNode->fMarkA = 0;
00459 
00460     // check if the number of divisors is not exceeded
00461     if ( Vec_PtrSize(p->vDivs) - Vec_PtrSize(vLeaves) + Vec_PtrSize(p->vTemp) >= Vec_PtrSize(p->vSims) - p->nLeavesMax )
00462         return 0;
00463 
00464     // get the number of divisors to collect
00465     Limit = Vec_PtrSize(p->vSims) - p->nLeavesMax - (Vec_PtrSize(p->vDivs) - Vec_PtrSize(vLeaves) + Vec_PtrSize(p->vTemp));
00466 
00467     // explore the fanouts, which are not in the MFFC
00468     Counter = 0;
00469     Vec_PtrForEachEntry( p->vDivs, pNode, i )
00470     {
00471         if ( Abc_ObjFanoutNum(pNode) > 100 )
00472         {
00473 //            printf( "%d ", Abc_ObjFanoutNum(pNode) );
00474             continue;
00475         }
00476         // if the fanout has both fanins in the set, add it
00477         Abc_ObjForEachFanout( pNode, pFanout, k )
00478         {
00479             if ( Abc_NodeIsTravIdCurrent(pFanout) || Abc_ObjIsCo(pFanout) || (int)pFanout->Level > Required )
00480                 continue;
00481             if ( Abc_NodeIsTravIdCurrent(Abc_ObjFanin0(pFanout)) && Abc_NodeIsTravIdCurrent(Abc_ObjFanin1(pFanout)) )
00482             {
00483                 if ( Abc_ObjFanin0(pFanout) == pRoot || Abc_ObjFanin1(pFanout) == pRoot )
00484                     continue;
00485                 Vec_PtrPush( p->vDivs, pFanout );
00486                 Abc_NodeSetTravIdCurrent( pFanout );
00487                 // quit computing divisors if there is too many of them
00488                 if ( ++Counter == Limit )
00489                     goto Quits;
00490             }
00491         }
00492     }
00493 
00494 Quits :
00495     // get the number of divisors
00496     p->nDivs = Vec_PtrSize(p->vDivs);
00497 
00498     // add the nodes in the MFFC
00499     Vec_PtrForEachEntry( p->vTemp, pNode, i )
00500         Vec_PtrPush( p->vDivs, pNode );
00501     assert( pRoot == Vec_PtrEntryLast(p->vDivs) );
00502 
00503     assert( Vec_PtrSize(p->vDivs) - Vec_PtrSize(vLeaves) <= Vec_PtrSize(p->vSims) - p->nLeavesMax );
00504     return 1;
00505 }

void Abc_ManResubCollectDivs_rec ( Abc_Obj_t *  pNode,
Vec_Ptr_t *  vInternal 
)

Function*************************************************************

Synopsis []

Description []

SideEffects []

SeeAlso []

Definition at line 408 of file abcResub.c.

00409 {
00410     // skip visited nodes
00411     if ( Abc_NodeIsTravIdCurrent(pNode) )
00412         return;
00413     Abc_NodeSetTravIdCurrent(pNode);
00414     // collect the fanins
00415     Abc_ManResubCollectDivs_rec( Abc_ObjFanin0(pNode), vInternal );
00416     Abc_ManResubCollectDivs_rec( Abc_ObjFanin1(pNode), vInternal );
00417     // collect the internal node
00418     if ( pNode->fMarkA == 0 ) 
00419         Vec_PtrPush( vInternal, pNode );
00420 }

Dec_Graph_t * Abc_ManResubDivs0 ( Abc_ManRes_t *  p  )  [static]

Function*************************************************************

Synopsis []

Description []

SideEffects []

SeeAlso []

Definition at line 1045 of file abcResub.c.

01046 {
01047     Abc_Obj_t * pObj;
01048     unsigned * puData, * puDataR;
01049     int i, w;
01050     puDataR = p->pRoot->pData;
01051     Vec_PtrForEachEntryStop( p->vDivs, pObj, i, p->nDivs )
01052     {
01053         puData = pObj->pData;
01054         for ( w = 0; w < p->nWords; w++ )
01055 //            if ( puData[w] != puDataR[w] )
01056             if ( (puData[w] ^ puDataR[w]) & p->pCareSet[w] ) // care set
01057                 break;
01058         if ( w == p->nWords )
01059             return Abc_ManResubQuit0( p->pRoot, pObj );
01060     }
01061     return NULL;
01062 }

Dec_Graph_t * Abc_ManResubDivs1 ( Abc_ManRes_t *  p,
int  Required 
) [static]

Function*************************************************************

Synopsis []

Description []

SideEffects []

SeeAlso []

Definition at line 1075 of file abcResub.c.

01076 {
01077     Abc_Obj_t * pObj0, * pObj1;
01078     unsigned * puData0, * puData1, * puDataR;
01079     int i, k, w;
01080     puDataR = p->pRoot->pData;
01081     // check positive unate divisors
01082     Vec_PtrForEachEntry( p->vDivs1UP, pObj0, i )
01083     {
01084         puData0 = pObj0->pData;
01085         Vec_PtrForEachEntryStart( p->vDivs1UP, pObj1, k, i + 1 )
01086         {
01087             puData1 = pObj1->pData;
01088             for ( w = 0; w < p->nWords; w++ )
01089 //                if ( (puData0[w] | puData1[w]) != puDataR[w] )
01090                 if ( ((puData0[w] | puData1[w]) ^ puDataR[w]) & p->pCareSet[w] ) // care set
01091                     break;
01092             if ( w == p->nWords )
01093             {
01094                 p->nUsedNode1Or++;
01095                 return Abc_ManResubQuit1( p->pRoot, pObj0, pObj1, 1 );
01096             }
01097         }
01098     }
01099     // check negative unate divisors
01100     Vec_PtrForEachEntry( p->vDivs1UN, pObj0, i )
01101     {
01102         puData0 = pObj0->pData;
01103         Vec_PtrForEachEntryStart( p->vDivs1UN, pObj1, k, i + 1 )
01104         {
01105             puData1 = pObj1->pData;
01106             for ( w = 0; w < p->nWords; w++ )
01107 //                if ( (puData0[w] & puData1[w]) != puDataR[w] )
01108                 if ( ((puData0[w] & puData1[w]) ^ puDataR[w]) & p->pCareSet[w] ) // care set
01109                     break;
01110             if ( w == p->nWords )
01111             {
01112                 p->nUsedNode1And++;
01113                 return Abc_ManResubQuit1( p->pRoot, pObj0, pObj1, 0 );
01114             }
01115         }
01116     }
01117     return NULL;
01118 }

Dec_Graph_t * Abc_ManResubDivs12 ( Abc_ManRes_t *  p,
int  Required 
) [static]

Function*************************************************************

Synopsis []

Description []

SideEffects []

SeeAlso []

Definition at line 1131 of file abcResub.c.

01132 {
01133     Abc_Obj_t * pObj0, * pObj1, * pObj2, * pObjMax, * pObjMin0, * pObjMin1;
01134     unsigned * puData0, * puData1, * puData2, * puDataR;
01135     int i, k, j, w, LevelMax;
01136     puDataR = p->pRoot->pData;
01137     // check positive unate divisors
01138     Vec_PtrForEachEntry( p->vDivs1UP, pObj0, i )
01139     {
01140         puData0 = pObj0->pData;
01141         Vec_PtrForEachEntryStart( p->vDivs1UP, pObj1, k, i + 1 )
01142         {
01143             puData1 = pObj1->pData;
01144             Vec_PtrForEachEntryStart( p->vDivs1UP, pObj2, j, k + 1 )
01145             {
01146                 puData2 = pObj2->pData;
01147                 for ( w = 0; w < p->nWords; w++ )
01148 //                    if ( (puData0[w] | puData1[w] | puData2[w]) != puDataR[w] )
01149                     if ( ((puData0[w] | puData1[w] | puData2[w]) ^ puDataR[w]) & p->pCareSet[w] ) // care set
01150                         break;
01151                 if ( w == p->nWords )
01152                 {
01153                     LevelMax = ABC_MAX( pObj0->Level, ABC_MAX(pObj1->Level, pObj2->Level) );
01154                     assert( LevelMax <= Required - 1 );
01155 
01156                     pObjMax = NULL;
01157                     if ( (int)pObj0->Level == LevelMax )
01158                         pObjMax = pObj0, pObjMin0 = pObj1, pObjMin1 = pObj2;
01159                     if ( (int)pObj1->Level == LevelMax )
01160                     {
01161                         if ( pObjMax ) continue;
01162                         pObjMax = pObj1, pObjMin0 = pObj0, pObjMin1 = pObj2;
01163                     }
01164                     if ( (int)pObj2->Level == LevelMax )
01165                     {
01166                         if ( pObjMax ) continue;
01167                         pObjMax = pObj2, pObjMin0 = pObj0, pObjMin1 = pObj1;
01168                     }
01169 
01170                     p->nUsedNode2Or++;
01171                     return Abc_ManResubQuit21( p->pRoot, pObjMin0, pObjMin1, pObjMax, 1 );
01172                 }
01173             }
01174         }
01175     }
01176     // check negative unate divisors
01177     Vec_PtrForEachEntry( p->vDivs1UN, pObj0, i )
01178     {
01179         puData0 = pObj0->pData;
01180         Vec_PtrForEachEntryStart( p->vDivs1UN, pObj1, k, i + 1 )
01181         {
01182             puData1 = pObj1->pData;
01183             Vec_PtrForEachEntryStart( p->vDivs1UN, pObj2, j, k + 1 )
01184             {
01185                 puData2 = pObj2->pData;
01186                 for ( w = 0; w < p->nWords; w++ )
01187 //                    if ( (puData0[w] & puData1[w] & puData2[w]) != puDataR[w] )
01188                     if ( ((puData0[w] & puData1[w] & puData2[w]) ^ puDataR[w]) & p->pCareSet[w] ) // care set
01189                         break;
01190                 if ( w == p->nWords )
01191                 {
01192                     LevelMax = ABC_MAX( pObj0->Level, ABC_MAX(pObj1->Level, pObj2->Level) );
01193                     assert( LevelMax <= Required - 1 );
01194 
01195                     pObjMax = NULL;
01196                     if ( (int)pObj0->Level == LevelMax )
01197                         pObjMax = pObj0, pObjMin0 = pObj1, pObjMin1 = pObj2;
01198                     if ( (int)pObj1->Level == LevelMax )
01199                     {
01200                         if ( pObjMax ) continue;
01201                         pObjMax = pObj1, pObjMin0 = pObj0, pObjMin1 = pObj2;
01202                     }
01203                     if ( (int)pObj2->Level == LevelMax )
01204                     {
01205                         if ( pObjMax ) continue;
01206                         pObjMax = pObj2, pObjMin0 = pObj0, pObjMin1 = pObj1;
01207                     }
01208 
01209                     p->nUsedNode2And++;
01210                     return Abc_ManResubQuit21( p->pRoot, pObjMin0, pObjMin1, pObjMax, 0 );
01211                 }
01212             }
01213         }
01214     }
01215     return NULL;
01216 }

Dec_Graph_t * Abc_ManResubDivs2 ( Abc_ManRes_t *  p,
int  Required 
) [static]

Function*************************************************************

Synopsis []

Description []

SideEffects []

SeeAlso []

Definition at line 1229 of file abcResub.c.

01230 {
01231     Abc_Obj_t * pObj0, * pObj1, * pObj2;
01232     unsigned * puData0, * puData1, * puData2, * puDataR;
01233     int i, k, w;
01234     puDataR = p->pRoot->pData;
01235     // check positive unate divisors
01236     Vec_PtrForEachEntry( p->vDivs1UP, pObj0, i )
01237     {
01238         puData0 = pObj0->pData;
01239         Vec_PtrForEachEntry( p->vDivs2UP0, pObj1, k )
01240         {
01241             pObj2 = Vec_PtrEntry( p->vDivs2UP1, k );
01242 
01243             puData1 = Abc_ObjRegular(pObj1)->pData;
01244             puData2 = Abc_ObjRegular(pObj2)->pData;
01245             if ( Abc_ObjIsComplement(pObj1) && Abc_ObjIsComplement(pObj2) )
01246             {
01247                 for ( w = 0; w < p->nWords; w++ )
01248 //                    if ( (puData0[w] | (puData1[w] | puData2[w])) != puDataR[w] )
01249                     if ( ((puData0[w] | (puData1[w] | puData2[w])) ^ puDataR[w]) & p->pCareSet[w] ) // care set
01250                         break;
01251             }
01252             else if ( Abc_ObjIsComplement(pObj1) )
01253             {
01254                 for ( w = 0; w < p->nWords; w++ )
01255 //                    if ( (puData0[w] | (~puData1[w] & puData2[w])) != puDataR[w] )
01256                     if ( ((puData0[w] | (~puData1[w] & puData2[w])) ^ puDataR[w]) & p->pCareSet[w] ) // care set
01257                         break;
01258             }
01259             else if ( Abc_ObjIsComplement(pObj2) )
01260             {
01261                 for ( w = 0; w < p->nWords; w++ )
01262 //                    if ( (puData0[w] | (puData1[w] & ~puData2[w])) != puDataR[w] )
01263                     if ( ((puData0[w] | (puData1[w] & ~puData2[w])) ^ puDataR[w]) & p->pCareSet[w] ) // care set
01264                         break;
01265             }
01266             else 
01267             {
01268                 for ( w = 0; w < p->nWords; w++ )
01269 //                    if ( (puData0[w] | (puData1[w] & puData2[w])) != puDataR[w] )
01270                     if ( ((puData0[w] | (puData1[w] & puData2[w])) ^ puDataR[w]) & p->pCareSet[w] ) // care set
01271                         break;
01272             }
01273             if ( w == p->nWords )
01274             {
01275                 p->nUsedNode2OrAnd++;
01276                 return Abc_ManResubQuit2( p->pRoot, pObj0, pObj1, pObj2, 1 );
01277             }
01278         }
01279     }
01280     // check negative unate divisors
01281     Vec_PtrForEachEntry( p->vDivs1UN, pObj0, i )
01282     {
01283         puData0 = pObj0->pData;
01284         Vec_PtrForEachEntry( p->vDivs2UN0, pObj1, k )
01285         {
01286             pObj2 = Vec_PtrEntry( p->vDivs2UN1, k );
01287 
01288             puData1 = Abc_ObjRegular(pObj1)->pData;
01289             puData2 = Abc_ObjRegular(pObj2)->pData;
01290             if ( Abc_ObjIsComplement(pObj1) && Abc_ObjIsComplement(pObj2) )
01291             {
01292                 for ( w = 0; w < p->nWords; w++ )
01293 //                    if ( (puData0[w] & (puData1[w] | puData2[w])) != puDataR[w] )
01294                     if ( ((puData0[w] & (puData1[w] | puData2[w])) ^ puDataR[w]) & p->pCareSet[w] ) // care set
01295                         break;
01296             }
01297             else if ( Abc_ObjIsComplement(pObj1) )
01298             {
01299                 for ( w = 0; w < p->nWords; w++ )
01300 //                    if ( (puData0[w] & (~puData1[w] & puData2[w])) != puDataR[w] )
01301                     if ( ((puData0[w] & (~puData1[w] & puData2[w])) ^ puDataR[w]) & p->pCareSet[w] ) // care set
01302                         break;
01303             }
01304             else if ( Abc_ObjIsComplement(pObj2) )
01305             {
01306                 for ( w = 0; w < p->nWords; w++ )
01307 //                    if ( (puData0[w] & (puData1[w] & ~puData2[w])) != puDataR[w] )
01308                     if ( ((puData0[w] & (puData1[w] & ~puData2[w])) ^ puDataR[w]) & p->pCareSet[w] ) // care set
01309                         break;
01310             }
01311             else 
01312             {
01313                 for ( w = 0; w < p->nWords; w++ )
01314 //                    if ( (puData0[w] & (puData1[w] & puData2[w])) != puDataR[w] )
01315                     if ( ((puData0[w] & (puData1[w] & puData2[w])) ^ puDataR[w]) & p->pCareSet[w] ) // care set
01316                         break;
01317             }
01318             if ( w == p->nWords )
01319             {
01320                 p->nUsedNode2AndOr++;
01321                 return Abc_ManResubQuit2( p->pRoot, pObj0, pObj1, pObj2, 0 );
01322             }
01323         }
01324     }
01325     return NULL;
01326 }

Dec_Graph_t * Abc_ManResubDivs3 ( Abc_ManRes_t *  p,
int  Required 
) [static]

Function*************************************************************

Synopsis []

Description []

SideEffects []

SeeAlso []

Definition at line 1339 of file abcResub.c.

01340 {
01341     Abc_Obj_t * pObj0, * pObj1, * pObj2, * pObj3;
01342     unsigned * puData0, * puData1, * puData2, * puData3, * puDataR;
01343     int i, k, w, Flag;
01344     puDataR = p->pRoot->pData;
01345     // check positive unate divisors
01346     Vec_PtrForEachEntry( p->vDivs2UP0, pObj0, i )
01347     {
01348         pObj1 = Vec_PtrEntry( p->vDivs2UP1, i );
01349         puData0 = Abc_ObjRegular(pObj0)->pData;
01350         puData1 = Abc_ObjRegular(pObj1)->pData;
01351         Flag = (Abc_ObjIsComplement(pObj0) << 3) | (Abc_ObjIsComplement(pObj1) << 2);
01352 
01353         Vec_PtrForEachEntryStart( p->vDivs2UP0, pObj2, k, i + 1 )
01354         {
01355             pObj3 = Vec_PtrEntry( p->vDivs2UP1, k );
01356             puData2 = Abc_ObjRegular(pObj2)->pData;
01357             puData3 = Abc_ObjRegular(pObj3)->pData;
01358 
01359             Flag = (Flag & 12) | (Abc_ObjIsComplement(pObj2) << 1) | Abc_ObjIsComplement(pObj3);
01360             assert( Flag < 16 );
01361             switch( Flag )
01362             {
01363             case 0: // 0000
01364                 for ( w = 0; w < p->nWords; w++ )
01365 //                    if ( ((puData0[w] & puData1[w]) | (puData2[w] & puData3[w])) != puDataR[w] )
01366                     if ( (((puData0[w] & puData1[w]) | (puData2[w] & puData3[w])) ^ puDataR[w]) & p->pCareSet[w] ) // care set
01367                         break;
01368                 break;
01369             case 1: // 0001
01370                 for ( w = 0; w < p->nWords; w++ )
01371 //                    if ( ((puData0[w] & puData1[w]) | (puData2[w] & ~puData3[w])) != puDataR[w] )
01372                     if ( (((puData0[w] & puData1[w]) | (puData2[w] & ~puData3[w])) ^ puDataR[w]) & p->pCareSet[w] ) // care set
01373                         break;
01374                 break;
01375             case 2: // 0010
01376                 for ( w = 0; w < p->nWords; w++ )
01377 //                    if ( ((puData0[w] & puData1[w]) | (~puData2[w] & puData3[w])) != puDataR[w] )
01378                     if ( (((puData0[w] & puData1[w]) | (~puData2[w] & puData3[w])) ^ puDataR[w]) & p->pCareSet[w] ) // care set
01379                         break;
01380                 break;
01381             case 3: // 0011
01382                 for ( w = 0; w < p->nWords; w++ )
01383 //                    if ( ((puData0[w] & puData1[w]) | (puData2[w] | puData3[w])) != puDataR[w] )
01384                     if ( (((puData0[w] & puData1[w]) | (puData2[w] | puData3[w])) ^ puDataR[w]) & p->pCareSet[w] ) // care set
01385                         break;
01386                 break;
01387 
01388             case 4: // 0100
01389                 for ( w = 0; w < p->nWords; w++ )
01390 //                    if ( ((puData0[w] & ~puData1[w]) | (puData2[w] & puData3[w])) != puDataR[w] )
01391                     if ( (((puData0[w] & ~puData1[w]) | (puData2[w] & puData3[w])) ^ puDataR[w]) & p->pCareSet[w] ) // care set
01392                         break;
01393                 break;
01394             case 5: // 0101
01395                 for ( w = 0; w < p->nWords; w++ )
01396 //                    if ( ((puData0[w] & ~puData1[w]) | (puData2[w] & ~puData3[w])) != puDataR[w] )
01397                     if ( (((puData0[w] & ~puData1[w]) | (puData2[w] & ~puData3[w])) ^ puDataR[w]) & p->pCareSet[w] ) // care set
01398                         break;
01399                 break;
01400             case 6: // 0110
01401                 for ( w = 0; w < p->nWords; w++ )
01402 //                    if ( ((puData0[w] & ~puData1[w]) | (~puData2[w] & puData3[w])) != puDataR[w] )
01403                     if ( (((puData0[w] & ~puData1[w]) | (~puData2[w] & puData3[w])) ^ puDataR[w]) & p->pCareSet[w] ) // care set
01404                         break;
01405                 break;
01406             case 7: // 0111
01407                 for ( w = 0; w < p->nWords; w++ )
01408 //                    if ( ((puData0[w] & ~puData1[w]) | (puData2[w] | puData3[w])) != puDataR[w] )
01409                     if ( (((puData0[w] & ~puData1[w]) | (puData2[w] | puData3[w])) ^ puDataR[w]) & p->pCareSet[w] ) // care set
01410                         break;
01411                 break;
01412 
01413             case 8: // 1000
01414                 for ( w = 0; w < p->nWords; w++ )
01415 //                    if ( ((~puData0[w] & puData1[w]) | (puData2[w] & puData3[w])) != puDataR[w] )
01416                     if ( (((~puData0[w] & puData1[w]) | (puData2[w] & puData3[w])) ^ puDataR[w]) & p->pCareSet[w] ) // care set
01417                         break;
01418                 break;
01419             case 9: // 1001
01420                 for ( w = 0; w < p->nWords; w++ )
01421 //                    if ( ((~puData0[w] & puData1[w]) | (puData2[w] & ~puData3[w])) != puDataR[w] )
01422                     if ( (((~puData0[w] & puData1[w]) | (puData2[w] & ~puData3[w])) ^ puDataR[w]) & p->pCareSet[w] ) // care set
01423                         break;
01424                 break;
01425             case 10: // 1010
01426                 for ( w = 0; w < p->nWords; w++ )
01427 //                    if ( ((~puData0[w] & puData1[w]) | (~puData2[w] & puData3[w])) != puDataR[w] )
01428                     if ( (((~puData0[w] & puData1[w]) | (~puData2[w] & puData3[w])) ^ puDataR[w]) & p->pCareSet[w] ) // care set
01429                         break;
01430                 break;
01431             case 11: // 1011
01432                 for ( w = 0; w < p->nWords; w++ )
01433 //                    if ( ((~puData0[w] & puData1[w]) | (puData2[w] | puData3[w])) != puDataR[w] )
01434                     if ( (((~puData0[w] & puData1[w]) | (puData2[w] | puData3[w])) ^ puDataR[w]) & p->pCareSet[w] ) // care set
01435                         break;
01436                 break;
01437 
01438             case 12: // 1100
01439                 for ( w = 0; w < p->nWords; w++ )
01440 //                    if ( ((puData0[w] | puData1[w]) | (puData2[w] & puData3[w])) != puDataR[w] )
01441                     if ( (((puData0[w] | puData1[w]) | (puData2[w] & puData3[w])) ^ puDataR[w]) & p->pCareSet[w] ) // care set
01442                         break;
01443                 break;
01444             case 13: // 1101
01445                 for ( w = 0; w < p->nWords; w++ )
01446 //                    if ( ((puData0[w] | puData1[w]) | (puData2[w] & ~puData3[w])) != puDataR[w] )
01447                     if ( (((puData0[w] | puData1[w]) | (puData2[w] & ~puData3[w])) ^ puDataR[w]) & p->pCareSet[w] )
01448                         break;
01449                 break;
01450             case 14: // 1110
01451                 for ( w = 0; w < p->nWords; w++ )
01452 //                    if ( ((puData0[w] | puData1[w]) | (~puData2[w] & puData3[w])) != puDataR[w] )
01453                     if ( (((puData0[w] | puData1[w]) | (~puData2[w] & puData3[w])) ^ puDataR[w]) & p->pCareSet[w] )
01454                         break;
01455                 break;
01456             case 15: // 1111
01457                 for ( w = 0; w < p->nWords; w++ )
01458 //                    if ( ((puData0[w] | puData1[w]) | (puData2[w] | puData3[w])) != puDataR[w] )
01459                     if ( (((puData0[w] | puData1[w]) | (puData2[w] | puData3[w])) ^ puDataR[w]) & p->pCareSet[w] )
01460                         break;
01461                 break;
01462 
01463             }
01464             if ( w == p->nWords )
01465             {
01466                 p->nUsedNode3OrAnd++;
01467                 return Abc_ManResubQuit3( p->pRoot, pObj0, pObj1, pObj2, pObj3, 1 );
01468             }
01469         }
01470     }
01471 /*
01472     // check negative unate divisors
01473     Vec_PtrForEachEntry( p->vDivs2UN0, pObj0, i )
01474     {
01475         pObj1 = Vec_PtrEntry( p->vDivs2UN1, i );
01476         puData0 = Abc_ObjRegular(pObj0)->pData;
01477         puData1 = Abc_ObjRegular(pObj1)->pData;
01478         Flag = (Abc_ObjIsComplement(pObj0) << 3) | (Abc_ObjIsComplement(pObj1) << 2);
01479 
01480         Vec_PtrForEachEntryStart( p->vDivs2UN0, pObj2, k, i + 1 )
01481         {
01482             pObj3 = Vec_PtrEntry( p->vDivs2UN1, k );
01483             puData2 = Abc_ObjRegular(pObj2)->pData;
01484             puData3 = Abc_ObjRegular(pObj3)->pData;
01485 
01486             Flag = (Flag & 12) | (Abc_ObjIsComplement(pObj2) << 1) | Abc_ObjIsComplement(pObj3);
01487             assert( Flag < 16 );
01488             switch( Flag )
01489             {
01490             case 0: // 0000
01491                 for ( w = 0; w < p->nWords; w++ )
01492                     if ( ((puData0[w] & puData1[w]) & (puData2[w] & puData3[w])) != puDataR[w] )
01493                         break;
01494                 break;
01495             case 1: // 0001
01496                 for ( w = 0; w < p->nWords; w++ )
01497                     if ( ((puData0[w] & puData1[w]) & (puData2[w] & ~puData3[w])) != puDataR[w] )
01498                         break;
01499                 break;
01500             case 2: // 0010
01501                 for ( w = 0; w < p->nWords; w++ )
01502                     if ( ((puData0[w] & puData1[w]) & (~puData2[w] & puData3[w])) != puDataR[w] )
01503                         break;
01504                 break;
01505             case 3: // 0011
01506                 for ( w = 0; w < p->nWords; w++ )
01507                     if ( ((puData0[w] & puData1[w]) & (puData2[w] | puData3[w])) != puDataR[w] )
01508                         break;
01509                 break;
01510 
01511             case 4: // 0100
01512                 for ( w = 0; w < p->nWords; w++ )
01513                     if ( ((puData0[w] & ~puData1[w]) & (puData2[w] & puData3[w])) != puDataR[w] )
01514                         break;
01515                 break;
01516             case 5: // 0101
01517                 for ( w = 0; w < p->nWords; w++ )
01518                     if ( ((puData0[w] & ~puData1[w]) & (puData2[w] & ~puData3[w])) != puDataR[w] )
01519                         break;
01520                 break;
01521             case 6: // 0110
01522                 for ( w = 0; w < p->nWords; w++ )
01523                     if ( ((puData0[w] & ~puData1[w]) & (~puData2[w] & puData3[w])) != puDataR[w] )
01524                         break;
01525                 break;
01526             case 7: // 0111
01527                 for ( w = 0; w < p->nWords; w++ )
01528                     if ( ((puData0[w] & ~puData1[w]) & (puData2[w] | puData3[w])) != puDataR[w] )
01529                         break;
01530                 break;
01531 
01532             case 8: // 1000
01533                 for ( w = 0; w < p->nWords; w++ )
01534                     if ( ((~puData0[w] & puData1[w]) & (puData2[w] & puData3[w])) != puDataR[w] )
01535                         break;
01536                 break;
01537             case 9: // 1001
01538                 for ( w = 0; w < p->nWords; w++ )
01539                     if ( ((~puData0[w] & puData1[w]) & (puData2[w] & ~puData3[w])) != puDataR[w] )
01540                         break;
01541                 break;
01542             case 10: // 1010
01543                 for ( w = 0; w < p->nWords; w++ )
01544                     if ( ((~puData0[w] & puData1[w]) & (~puData2[w] & puData3[w])) != puDataR[w] )
01545                         break;
01546                 break;
01547             case 11: // 1011
01548                 for ( w = 0; w < p->nWords; w++ )
01549                     if ( ((~puData0[w] & puData1[w]) & (puData2[w] | puData3[w])) != puDataR[w] )
01550                         break;
01551                 break;
01552 
01553             case 12: // 1100
01554                 for ( w = 0; w < p->nWords; w++ )
01555                     if ( ((puData0[w] | puData1[w]) & (puData2[w] & puData3[w])) != puDataR[w] )
01556                         break;
01557                 break;
01558             case 13: // 1101
01559                 for ( w = 0; w < p->nWords; w++ )
01560                     if ( ((puData0[w] | puData1[w]) & (puData2[w] & ~puData3[w])) != puDataR[w] )
01561                         break;
01562                 break;
01563             case 14: // 1110
01564                 for ( w = 0; w < p->nWords; w++ )
01565                     if ( ((puData0[w] | puData1[w]) & (~puData2[w] & puData3[w])) != puDataR[w] )
01566                         break;
01567                 break;
01568             case 15: // 1111
01569                 for ( w = 0; w < p->nWords; w++ )
01570                     if ( ((puData0[w] | puData1[w]) & (puData2[w] | puData3[w])) != puDataR[w] )
01571                         break;
01572                 break;
01573 
01574             }
01575             if ( w == p->nWords )
01576             {
01577                 p->nUsedNode3AndOr++;
01578                 return Abc_ManResubQuit3( p->pRoot, pObj0, pObj1, pObj2, pObj3, 0 );
01579             }
01580         }
01581     }
01582 */
01583     return NULL;
01584 }

void Abc_ManResubDivsD ( Abc_ManRes_t *  p,
int  Required 
) [static]

Function*************************************************************

Synopsis [Derives double-node unate/binate divisors.]

Description []

SideEffects []

SeeAlso []

Definition at line 892 of file abcResub.c.

00893 {
00894     Abc_Obj_t * pObj0, * pObj1;
00895     unsigned * puData0, * puData1, * puDataR;
00896     int i, k, w;
00897     Vec_PtrClear( p->vDivs2UP0 );
00898     Vec_PtrClear( p->vDivs2UP1 );
00899     Vec_PtrClear( p->vDivs2UN0 );
00900     Vec_PtrClear( p->vDivs2UN1 );
00901     puDataR = p->pRoot->pData;
00902     Vec_PtrForEachEntry( p->vDivs1B, pObj0, i )
00903     {
00904         if ( (int)pObj0->Level > Required - 2 )
00905             continue;
00906 
00907         puData0 = pObj0->pData;
00908         Vec_PtrForEachEntryStart( p->vDivs1B, pObj1, k, i + 1 )
00909         {
00910             if ( (int)pObj1->Level > Required - 2 )
00911                 continue;
00912 
00913             puData1 = pObj1->pData;
00914 
00915             if ( Vec_PtrSize(p->vDivs2UP0) < ABC_RS_DIV2_MAX )
00916             {
00917                 // get positive unate divisors
00918                 for ( w = 0; w < p->nWords; w++ )
00919 //                    if ( (puData0[w] & puData1[w]) & ~puDataR[w] )
00920                     if ( (puData0[w] & puData1[w]) & ~puDataR[w] & p->pCareSet[w] ) // care set
00921                         break;
00922                 if ( w == p->nWords )
00923                 {
00924                     Vec_PtrPush( p->vDivs2UP0, pObj0 );
00925                     Vec_PtrPush( p->vDivs2UP1, pObj1 );
00926                 }
00927                 for ( w = 0; w < p->nWords; w++ )
00928 //                    if ( (~puData0[w] & puData1[w]) & ~puDataR[w] )
00929                     if ( (~puData0[w] & puData1[w]) & ~puDataR[w] & p->pCareSet[w] ) // care set
00930                         break;
00931                 if ( w == p->nWords )
00932                 {
00933                     Vec_PtrPush( p->vDivs2UP0, Abc_ObjNot(pObj0) );
00934                     Vec_PtrPush( p->vDivs2UP1, pObj1 );
00935                 }
00936                 for ( w = 0; w < p->nWords; w++ )
00937 //                    if ( (puData0[w] & ~puData1[w]) & ~puDataR[w] )
00938                     if ( (puData0[w] & ~puData1[w]) & ~puDataR[w] & p->pCareSet[w] ) // care set
00939                         break;
00940                 if ( w == p->nWords )
00941                 {
00942                     Vec_PtrPush( p->vDivs2UP0, pObj0 );
00943                     Vec_PtrPush( p->vDivs2UP1, Abc_ObjNot(pObj1) );
00944                 }
00945                 for ( w = 0; w < p->nWords; w++ )
00946 //                    if ( (puData0[w] | puData1[w]) & ~puDataR[w] )
00947                     if ( (puData0[w] | puData1[w]) & ~puDataR[w] & p->pCareSet[w] ) // care set
00948                         break;
00949                 if ( w == p->nWords )
00950                 {
00951                     Vec_PtrPush( p->vDivs2UP0, Abc_ObjNot(pObj0) );
00952                     Vec_PtrPush( p->vDivs2UP1, Abc_ObjNot(pObj1) );
00953                 }
00954             }
00955 
00956             if ( Vec_PtrSize(p->vDivs2UN0) < ABC_RS_DIV2_MAX )
00957             {
00958                 // get negative unate divisors
00959                 for ( w = 0; w < p->nWords; w++ )
00960 //                    if ( ~(puData0[w] & puData1[w]) & puDataR[w] )
00961                     if ( ~(puData0[w] & puData1[w]) & puDataR[w] & p->pCareSet[w] ) // care set
00962                         break;
00963                 if ( w == p->nWords )
00964                 {
00965                     Vec_PtrPush( p->vDivs2UN0, pObj0 );
00966                     Vec_PtrPush( p->vDivs2UN1, pObj1 );
00967                 }
00968                 for ( w = 0; w < p->nWords; w++ )
00969 //                    if ( ~(~puData0[w] & puData1[w]) & puDataR[w] )
00970                     if ( ~(~puData0[w] & puData1[w]) & puDataR[w] & p->pCareSet[w] ) // care set
00971                         break;
00972                 if ( w == p->nWords )
00973                 {
00974                     Vec_PtrPush( p->vDivs2UN0, Abc_ObjNot(pObj0) );
00975                     Vec_PtrPush( p->vDivs2UN1, pObj1 );
00976                 }
00977                 for ( w = 0; w < p->nWords; w++ )
00978 //                    if ( ~(puData0[w] & ~puData1[w]) & puDataR[w] )
00979                     if ( ~(puData0[w] & ~puData1[w]) & puDataR[w] & p->pCareSet[w] ) // care set
00980                         break;
00981                 if ( w == p->nWords )
00982                 {
00983                     Vec_PtrPush( p->vDivs2UN0, pObj0 );
00984                     Vec_PtrPush( p->vDivs2UN1, Abc_ObjNot(pObj1) );
00985                 }
00986                 for ( w = 0; w < p->nWords; w++ )
00987 //                    if ( ~(puData0[w] | puData1[w]) & puDataR[w] )
00988                     if ( ~(puData0[w] | puData1[w]) & puDataR[w] & p->pCareSet[w] ) // care set
00989                         break;
00990                 if ( w == p->nWords )
00991                 {
00992                     Vec_PtrPush( p->vDivs2UN0, Abc_ObjNot(pObj0) );
00993                     Vec_PtrPush( p->vDivs2UN1, Abc_ObjNot(pObj1) );
00994                 }
00995             }
00996         }
00997     }
00998 //    printf( "%d %d  ", Vec_PtrSize(p->vDivs2UP0), Vec_PtrSize(p->vDivs2UN0) );
00999 }

void Abc_ManResubDivsS ( Abc_ManRes_t *  p,
int  Required 
) [static]

Function*************************************************************

Synopsis [Derives single-node unate/binate divisors.]

Description []

SideEffects []

SeeAlso []

Definition at line 841 of file abcResub.c.

00842 {
00843     Abc_Obj_t * pObj;
00844     unsigned * puData, * puDataR;
00845     int i, w;
00846     Vec_PtrClear( p->vDivs1UP );
00847     Vec_PtrClear( p->vDivs1UN );
00848     Vec_PtrClear( p->vDivs1B );
00849     puDataR = p->pRoot->pData;
00850     Vec_PtrForEachEntryStop( p->vDivs, pObj, i, p->nDivs )
00851     {
00852         if ( (int)pObj->Level > Required - 1 )
00853             continue;
00854 
00855         puData = pObj->pData;
00856         // check positive containment
00857         for ( w = 0; w < p->nWords; w++ )
00858 //            if ( puData[w] & ~puDataR[w] )
00859             if ( puData[w] & ~puDataR[w] & p->pCareSet[w] ) // care set
00860                 break;
00861         if ( w == p->nWords )
00862         {
00863             Vec_PtrPush( p->vDivs1UP, pObj );
00864             continue;
00865         }
00866         // check negative containment
00867         for ( w = 0; w < p->nWords; w++ )
00868 //            if ( ~puData[w] & puDataR[w] )
00869             if ( ~puData[w] & puDataR[w] & p->pCareSet[w] ) // care set
00870                 break;
00871         if ( w == p->nWords )
00872         {
00873             Vec_PtrPush( p->vDivs1UN, pObj );
00874             continue;
00875         }
00876         // add the node to binates
00877         Vec_PtrPush( p->vDivs1B, pObj );
00878     }
00879 }

Dec_Graph_t * Abc_ManResubEval ( Abc_ManRes_t *  p,
Abc_Obj_t *  pRoot,
Vec_Ptr_t *  vLeaves,
int  nSteps,
bool  fUpdateLevel,
bool  fVerbose 
) [static]

Function*************************************************************

Synopsis [Evaluates resubstution of one cut.]

Description [Returns the graph to add if any.]

SideEffects []

SeeAlso []

Definition at line 1618 of file abcResub.c.

01619 {
01620     extern int Abc_NodeMffsInside( Abc_Obj_t * pNode, Vec_Ptr_t * vLeaves, Vec_Ptr_t * vInside );
01621     Dec_Graph_t * pGraph;
01622     int Required;
01623     int clk;
01624 
01625     Required = fUpdateLevel? Abc_ObjRequiredLevel(pRoot) : ABC_INFINITY;
01626 
01627     assert( nSteps >= 0 );
01628     assert( nSteps <= 3 );
01629     p->pRoot = pRoot;
01630     p->nLeaves = Vec_PtrSize(vLeaves);
01631     p->nLastGain = -1;
01632 
01633     // collect the MFFC
01634 clk = clock();
01635     p->nMffc = Abc_NodeMffsInside( pRoot, vLeaves, p->vTemp );
01636 p->timeMffc += clock() - clk;
01637     assert( p->nMffc > 0 );
01638 
01639     // collect the divisor nodes
01640 clk = clock();
01641     if ( !Abc_ManResubCollectDivs( p, pRoot, vLeaves, Required ) )
01642         return NULL;
01643     p->timeDiv += clock() - clk;
01644 
01645     p->nTotalDivs   += p->nDivs;
01646     p->nTotalLeaves += p->nLeaves;
01647 
01648     // simulate the nodes
01649 clk = clock();
01650     Abc_ManResubSimulate( p->vDivs, p->nLeaves, p->vSims, p->nLeavesMax, p->nWords );
01651 p->timeSim += clock() - clk;
01652 
01653 clk = clock();
01654     // consider constants
01655     if ( pGraph = Abc_ManResubQuit( p ) )
01656     {
01657         p->nUsedNodeC++;
01658         p->nLastGain = p->nMffc;
01659         return pGraph;
01660     }
01661 
01662     // consider equal nodes
01663     if ( pGraph = Abc_ManResubDivs0( p ) )
01664     {
01665 p->timeRes1 += clock() - clk;
01666         p->nUsedNode0++;
01667         p->nLastGain = p->nMffc;
01668         return pGraph;
01669     }
01670     if ( nSteps == 0 || p->nMffc == 1 )
01671     {
01672 p->timeRes1 += clock() - clk;
01673         return NULL;
01674     }
01675 
01676     // get the one level divisors
01677     Abc_ManResubDivsS( p, Required );
01678 
01679     // consider one node
01680     if ( pGraph = Abc_ManResubDivs1( p, Required ) )
01681     {
01682 p->timeRes1 += clock() - clk;
01683         p->nLastGain = p->nMffc - 1;
01684         return pGraph;
01685     }
01686 p->timeRes1 += clock() - clk;
01687     if ( nSteps == 1 || p->nMffc == 2 )
01688         return NULL;
01689 
01690 clk = clock();
01691     // consider triples
01692     if ( pGraph = Abc_ManResubDivs12( p, Required ) )
01693     {
01694 p->timeRes2 += clock() - clk;
01695         p->nLastGain = p->nMffc - 2;
01696         return pGraph;
01697     }
01698 p->timeRes2 += clock() - clk;
01699 
01700     // get the two level divisors
01701 clk = clock();
01702     Abc_ManResubDivsD( p, Required );
01703 p->timeResD += clock() - clk;
01704 
01705     // consider two nodes
01706 clk = clock();
01707     if ( pGraph = Abc_ManResubDivs2( p, Required ) )
01708     {
01709 p->timeRes2 += clock() - clk;
01710         p->nLastGain = p->nMffc - 2;
01711         return pGraph;
01712     }
01713 p->timeRes2 += clock() - clk;
01714     if ( nSteps == 2 || p->nMffc == 3 )
01715         return NULL;
01716 
01717     // consider two nodes
01718 clk = clock();
01719     if ( pGraph = Abc_ManResubDivs3( p, Required ) )
01720     {
01721 p->timeRes3 += clock() - clk;
01722         p->nLastGain = p->nMffc - 3;
01723         return pGraph;
01724     }
01725 p->timeRes3 += clock() - clk;
01726     if ( nSteps == 3 || p->nLeavesMax == 4 )
01727         return NULL;
01728     return NULL;
01729 }

void Abc_ManResubPrint ( Abc_ManRes_t *  p  )  [static]

Function*************************************************************

Synopsis []

Description []

SideEffects []

SeeAlso []

Definition at line 367 of file abcResub.c.

00368 {
00369     printf( "Used constants    = %6d.             ", p->nUsedNodeC );          PRT( "Cuts  ", p->timeCut );
00370     printf( "Used replacements = %6d.             ", p->nUsedNode0 );          PRT( "Resub ", p->timeRes );
00371     printf( "Used single ORs   = %6d.             ", p->nUsedNode1Or );        PRT( " Div  ", p->timeDiv );
00372     printf( "Used single ANDs  = %6d.             ", p->nUsedNode1And );       PRT( " Mffc ", p->timeMffc );
00373     printf( "Used double ORs   = %6d.             ", p->nUsedNode2Or );        PRT( " Sim  ", p->timeSim );
00374     printf( "Used double ANDs  = %6d.             ", p->nUsedNode2And );       PRT( " 1    ", p->timeRes1 );
00375     printf( "Used OR-AND       = %6d.             ", p->nUsedNode2OrAnd );     PRT( " D    ", p->timeResD );
00376     printf( "Used AND-OR       = %6d.             ", p->nUsedNode2AndOr );     PRT( " 2    ", p->timeRes2 );
00377     printf( "Used OR-2ANDs     = %6d.             ", p->nUsedNode3OrAnd );     PRT( "Truth ", p->timeTruth ); //PRT( " 3    ", p->timeRes3 );
00378     printf( "Used AND-2ORs     = %6d.             ", p->nUsedNode3AndOr );     PRT( "AIG   ", p->timeNtk );
00379     printf( "TOTAL             = %6d.             ", p->nUsedNodeC +
00380                                                      p->nUsedNode0 +
00381                                                      p->nUsedNode1Or +
00382                                                      p->nUsedNode1And +
00383                                                      p->nUsedNode2Or +
00384                                                      p->nUsedNode2And +
00385                                                      p->nUsedNode2OrAnd +
00386                                                      p->nUsedNode2AndOr +
00387                                                      p->nUsedNode3OrAnd +
00388                                                      p->nUsedNode3AndOr
00389                                                    );                          PRT( "TOTAL ", p->timeTotal );
00390     printf( "Total leaves   = %8d.\n", p->nTotalLeaves );
00391     printf( "Total divisors = %8d.\n", p->nTotalDivs );
00392 //    printf( "Total gain     = %8d.\n", p->nTotalGain );
00393     printf( "Gain           = %8d. (%6.2f %%).\n", p->nNodesBeg-p->nNodesEnd, 100.0*(p->nNodesBeg-p->nNodesEnd)/p->nNodesBeg );
00394 }

void Abc_ManResubPrintDivs ( Abc_ManRes_t *  p,
Abc_Obj_t *  pRoot,
Vec_Ptr_t *  vLeaves 
) [static]

Function*************************************************************

Synopsis []

Description []

SideEffects []

SeeAlso []

Definition at line 518 of file abcResub.c.

00519 {
00520     Abc_Obj_t * pFanin, * pNode;
00521     int i, k;
00522     // print the nodes
00523     Vec_PtrForEachEntry( p->vDivs, pNode, i )
00524     {
00525         if ( i < Vec_PtrSize(vLeaves) )
00526         {
00527             printf( "%6d : %c\n", pNode->Id, 'a'+i );
00528             continue;
00529         }
00530         printf( "%6d : %2d = ", pNode->Id, i );
00531         // find the first fanin
00532         Vec_PtrForEachEntry( p->vDivs, pFanin, k )
00533             if ( Abc_ObjFanin0(pNode) == pFanin )
00534                 break;
00535         if ( k < Vec_PtrSize(vLeaves) )
00536             printf( "%c", 'a' + k );
00537         else
00538             printf( "%d", k );
00539         printf( "%s ", Abc_ObjFaninC0(pNode)? "\'" : "" );
00540         // find the second fanin
00541         Vec_PtrForEachEntry( p->vDivs, pFanin, k )
00542             if ( Abc_ObjFanin1(pNode) == pFanin )
00543                 break;
00544         if ( k < Vec_PtrSize(vLeaves) )
00545             printf( "%c", 'a' + k );
00546         else
00547             printf( "%d", k );
00548         printf( "%s ", Abc_ObjFaninC1(pNode)? "\'" : "" );
00549         if ( pNode == pRoot )
00550             printf( " root" );
00551         printf( "\n" );
00552     }
00553     printf( "\n" );
00554 }

Dec_Graph_t * Abc_ManResubQuit ( Abc_ManRes_t *  p  )  [static]

Function*************************************************************

Synopsis []

Description []

SideEffects []

SeeAlso []

Definition at line 1014 of file abcResub.c.

01015 {
01016     Dec_Graph_t * pGraph;
01017     unsigned * upData;
01018     int w;
01019     upData = p->pRoot->pData;
01020     for ( w = 0; w < p->nWords; w++ )
01021 //        if ( upData[w] )
01022         if ( upData[w] & p->pCareSet[w] ) // care set
01023             break;
01024     if ( w != p->nWords )
01025         return NULL;
01026     // get constant node graph
01027     if ( p->pRoot->fPhase )
01028         pGraph = Dec_GraphCreateConst1();
01029     else 
01030         pGraph = Dec_GraphCreateConst0();
01031     return pGraph;
01032 }

Dec_Graph_t* Abc_ManResubQuit0 ( Abc_Obj_t *  pRoot,
Abc_Obj_t *  pObj 
)

Function*************************************************************

Synopsis []

Description []

SideEffects []

SeeAlso []

Definition at line 625 of file abcResub.c.

00626 {
00627     Dec_Graph_t * pGraph;
00628     Dec_Edge_t eRoot;
00629     pGraph = Dec_GraphCreate( 1 );
00630     Dec_GraphNode( pGraph, 0 )->pFunc = pObj;
00631     eRoot = Dec_EdgeCreate( 0, pObj->fPhase );
00632     Dec_GraphSetRoot( pGraph, eRoot );
00633     if ( pRoot->fPhase )
00634         Dec_GraphComplement( pGraph );
00635     return pGraph;
00636 }

Dec_Graph_t* Abc_ManResubQuit1 ( Abc_Obj_t *  pRoot,
Abc_Obj_t *  pObj0,
Abc_Obj_t *  pObj1,
int  fOrGate 
)

Function*************************************************************

Synopsis []

Description []

SideEffects []

SeeAlso []

Definition at line 649 of file abcResub.c.

00650 {
00651     Dec_Graph_t * pGraph;
00652     Dec_Edge_t eRoot, eNode0, eNode1;
00653     assert( pObj0 != pObj1 );
00654     assert( !Abc_ObjIsComplement(pObj0) );
00655     assert( !Abc_ObjIsComplement(pObj1) );
00656     pGraph = Dec_GraphCreate( 2 );
00657     Dec_GraphNode( pGraph, 0 )->pFunc = pObj0;
00658     Dec_GraphNode( pGraph, 1 )->pFunc = pObj1;
00659     eNode0 = Dec_EdgeCreate( 0, pObj0->fPhase );
00660     eNode1 = Dec_EdgeCreate( 1, pObj1->fPhase );
00661     if ( fOrGate ) 
00662         eRoot  = Dec_GraphAddNodeOr( pGraph, eNode0, eNode1 );
00663     else
00664         eRoot  = Dec_GraphAddNodeAnd( pGraph, eNode0, eNode1 );
00665     Dec_GraphSetRoot( pGraph, eRoot );
00666     if ( pRoot->fPhase )
00667         Dec_GraphComplement( pGraph );
00668     return pGraph;
00669 }

Dec_Graph_t* Abc_ManResubQuit2 ( Abc_Obj_t *  pRoot,
Abc_Obj_t *  pObj0,
Abc_Obj_t *  pObj1,
Abc_Obj_t *  pObj2,
int  fOrGate 
)

Function*************************************************************

Synopsis []

Description []

SideEffects []

SeeAlso []

Definition at line 724 of file abcResub.c.

00725 {
00726     Dec_Graph_t * pGraph;
00727     Dec_Edge_t eRoot, ePrev, eNode0, eNode1, eNode2;
00728     assert( pObj0 != pObj1 );
00729     assert( pObj0 != pObj2 );
00730     assert( pObj1 != pObj2 );
00731     assert( !Abc_ObjIsComplement(pObj0) );
00732     pGraph = Dec_GraphCreate( 3 );
00733     Dec_GraphNode( pGraph, 0 )->pFunc = Abc_ObjRegular(pObj0);
00734     Dec_GraphNode( pGraph, 1 )->pFunc = Abc_ObjRegular(pObj1);
00735     Dec_GraphNode( pGraph, 2 )->pFunc = Abc_ObjRegular(pObj2);
00736     eNode0 = Dec_EdgeCreate( 0, Abc_ObjRegular(pObj0)->fPhase );
00737     if ( Abc_ObjIsComplement(pObj1) && Abc_ObjIsComplement(pObj2) )
00738     {
00739         eNode1 = Dec_EdgeCreate( 1, Abc_ObjRegular(pObj1)->fPhase );
00740         eNode2 = Dec_EdgeCreate( 2, Abc_ObjRegular(pObj2)->fPhase );
00741         ePrev  = Dec_GraphAddNodeOr( pGraph, eNode1, eNode2 );
00742     }
00743     else
00744     {
00745         eNode1 = Dec_EdgeCreate( 1, Abc_ObjRegular(pObj1)->fPhase ^ Abc_ObjIsComplement(pObj1) );
00746         eNode2 = Dec_EdgeCreate( 2, Abc_ObjRegular(pObj2)->fPhase ^ Abc_ObjIsComplement(pObj2) );
00747         ePrev  = Dec_GraphAddNodeAnd( pGraph, eNode1, eNode2 );
00748     }
00749     if ( fOrGate ) 
00750         eRoot  = Dec_GraphAddNodeOr( pGraph, eNode0, ePrev );
00751     else
00752         eRoot  = Dec_GraphAddNodeAnd( pGraph, eNode0, ePrev );
00753     Dec_GraphSetRoot( pGraph, eRoot );
00754     if ( pRoot->fPhase )
00755         Dec_GraphComplement( pGraph );
00756     return pGraph;
00757 }

Dec_Graph_t* Abc_ManResubQuit21 ( Abc_Obj_t *  pRoot,
Abc_Obj_t *  pObj0,
Abc_Obj_t *  pObj1,
Abc_Obj_t *  pObj2,
int  fOrGate 
)

Function*************************************************************

Synopsis []

Description []

SideEffects []

SeeAlso []

Definition at line 682 of file abcResub.c.

00683 {
00684     Dec_Graph_t * pGraph;
00685     Dec_Edge_t eRoot, eNode0, eNode1, eNode2;
00686     assert( pObj0 != pObj1 );
00687     assert( !Abc_ObjIsComplement(pObj0) );
00688     assert( !Abc_ObjIsComplement(pObj1) );
00689     assert( !Abc_ObjIsComplement(pObj2) );
00690     pGraph = Dec_GraphCreate( 3 );
00691     Dec_GraphNode( pGraph, 0 )->pFunc = pObj0;
00692     Dec_GraphNode( pGraph, 1 )->pFunc = pObj1;
00693     Dec_GraphNode( pGraph, 2 )->pFunc = pObj2;
00694     eNode0 = Dec_EdgeCreate( 0, pObj0->fPhase );
00695     eNode1 = Dec_EdgeCreate( 1, pObj1->fPhase );
00696     eNode2 = Dec_EdgeCreate( 2, pObj2->fPhase );
00697     if ( fOrGate ) 
00698     {
00699         eRoot  = Dec_GraphAddNodeOr( pGraph, eNode0, eNode1 );
00700         eRoot  = Dec_GraphAddNodeOr( pGraph, eNode2, eRoot );
00701     }
00702     else
00703     {
00704         eRoot  = Dec_GraphAddNodeAnd( pGraph, eNode0, eNode1 );
00705         eRoot  = Dec_GraphAddNodeAnd( pGraph, eNode2, eRoot );
00706     }
00707     Dec_GraphSetRoot( pGraph, eRoot );
00708     if ( pRoot->fPhase )
00709         Dec_GraphComplement( pGraph );
00710     return pGraph;
00711 }

Dec_Graph_t* Abc_ManResubQuit3 ( Abc_Obj_t *  pRoot,
Abc_Obj_t *  pObj0,
Abc_Obj_t *  pObj1,
Abc_Obj_t *  pObj2,
Abc_Obj_t *  pObj3,
int  fOrGate 
)

Function*************************************************************

Synopsis []

Description []

SideEffects []

SeeAlso []

Definition at line 770 of file abcResub.c.

00771 {
00772     Dec_Graph_t * pGraph;
00773     Dec_Edge_t eRoot, ePrev0, ePrev1, eNode0, eNode1, eNode2, eNode3;
00774     assert( pObj0 != pObj1 );
00775     assert( pObj2 != pObj3 );
00776     pGraph = Dec_GraphCreate( 4 );
00777     Dec_GraphNode( pGraph, 0 )->pFunc = Abc_ObjRegular(pObj0);
00778     Dec_GraphNode( pGraph, 1 )->pFunc = Abc_ObjRegular(pObj1);
00779     Dec_GraphNode( pGraph, 2 )->pFunc = Abc_ObjRegular(pObj2);
00780     Dec_GraphNode( pGraph, 3 )->pFunc = Abc_ObjRegular(pObj3);
00781     if ( Abc_ObjIsComplement(pObj0) && Abc_ObjIsComplement(pObj1) )
00782     {
00783         eNode0 = Dec_EdgeCreate( 0, Abc_ObjRegular(pObj0)->fPhase );
00784         eNode1 = Dec_EdgeCreate( 1, Abc_ObjRegular(pObj1)->fPhase );
00785         ePrev0 = Dec_GraphAddNodeOr( pGraph, eNode0, eNode1 );
00786         if ( Abc_ObjIsComplement(pObj2) && Abc_ObjIsComplement(pObj3) )
00787         {
00788             eNode2 = Dec_EdgeCreate( 2, Abc_ObjRegular(pObj2)->fPhase );
00789             eNode3 = Dec_EdgeCreate( 3, Abc_ObjRegular(pObj3)->fPhase );
00790             ePrev1 = Dec_GraphAddNodeOr( pGraph, eNode2, eNode3 );
00791         }
00792         else
00793         {
00794             eNode2 = Dec_EdgeCreate( 2, Abc_ObjRegular(pObj2)->fPhase ^ Abc_ObjIsComplement(pObj2) );
00795             eNode3 = Dec_EdgeCreate( 3, Abc_ObjRegular(pObj3)->fPhase ^ Abc_ObjIsComplement(pObj3) );
00796             ePrev1 = Dec_GraphAddNodeAnd( pGraph, eNode2, eNode3 );
00797         }
00798     }
00799     else
00800     {
00801         eNode0 = Dec_EdgeCreate( 0, Abc_ObjRegular(pObj0)->fPhase ^ Abc_ObjIsComplement(pObj0) );
00802         eNode1 = Dec_EdgeCreate( 1, Abc_ObjRegular(pObj1)->fPhase ^ Abc_ObjIsComplement(pObj1) );
00803         ePrev0 = Dec_GraphAddNodeAnd( pGraph, eNode0, eNode1 );
00804         if ( Abc_ObjIsComplement(pObj2) && Abc_ObjIsComplement(pObj3) )
00805         {
00806             eNode2 = Dec_EdgeCreate( 2, Abc_ObjRegular(pObj2)->fPhase );
00807             eNode3 = Dec_EdgeCreate( 3, Abc_ObjRegular(pObj3)->fPhase );
00808             ePrev1 = Dec_GraphAddNodeOr( pGraph, eNode2, eNode3 );
00809         }
00810         else
00811         {
00812             eNode2 = Dec_EdgeCreate( 2, Abc_ObjRegular(pObj2)->fPhase ^ Abc_ObjIsComplement(pObj2) );
00813             eNode3 = Dec_EdgeCreate( 3, Abc_ObjRegular(pObj3)->fPhase ^ Abc_ObjIsComplement(pObj3) );
00814             ePrev1 = Dec_GraphAddNodeAnd( pGraph, eNode2, eNode3 );
00815         }
00816     }
00817     if ( fOrGate ) 
00818         eRoot = Dec_GraphAddNodeOr( pGraph, ePrev0, ePrev1 );
00819     else
00820         eRoot = Dec_GraphAddNodeAnd( pGraph, ePrev0, ePrev1 );
00821     Dec_GraphSetRoot( pGraph, eRoot );
00822     if ( pRoot->fPhase )
00823         Dec_GraphComplement( pGraph );
00824     return pGraph;
00825 }

void Abc_ManResubSimulate ( Vec_Ptr_t *  vDivs,
int  nLeaves,
Vec_Ptr_t *  vSims,
int  nLeavesMax,
int  nWords 
) [static]

Function*************************************************************

Synopsis [Performs simulation.]

Description []

SideEffects []

SeeAlso []

Definition at line 568 of file abcResub.c.

00569 {
00570     Abc_Obj_t * pObj;
00571     unsigned * puData0, * puData1, * puData;
00572     int i, k;
00573     assert( Vec_PtrSize(vDivs) - nLeaves <= Vec_PtrSize(vSims) - nLeavesMax );
00574     // simulate
00575     Vec_PtrForEachEntry( vDivs, pObj, i )
00576     {
00577         if ( i < nLeaves )
00578         { // initialize the leaf
00579             pObj->pData = Vec_PtrEntry( vSims, i );
00580             continue;
00581         }
00582         // set storage for the node's simulation info
00583         pObj->pData = Vec_PtrEntry( vSims, i - nLeaves + nLeavesMax );
00584         // get pointer to the simulation info
00585         puData  = pObj->pData;
00586         puData0 = Abc_ObjFanin0(pObj)->pData;
00587         puData1 = Abc_ObjFanin1(pObj)->pData;
00588         // simulate
00589         if ( Abc_ObjFaninC0(pObj) && Abc_ObjFaninC1(pObj) )
00590             for ( k = 0; k < nWords; k++ )
00591                 puData[k] = ~puData0[k] & ~puData1[k];
00592         else if ( Abc_ObjFaninC0(pObj) )
00593             for ( k = 0; k < nWords; k++ )
00594                 puData[k] = ~puData0[k] & puData1[k];
00595         else if ( Abc_ObjFaninC1(pObj) )
00596             for ( k = 0; k < nWords; k++ )
00597                 puData[k] = puData0[k] & ~puData1[k];
00598         else 
00599             for ( k = 0; k < nWords; k++ )
00600                 puData[k] = puData0[k] & puData1[k];
00601     }
00602     // normalize
00603     Vec_PtrForEachEntry( vDivs, pObj, i )
00604     {
00605         puData = pObj->pData;
00606         pObj->fPhase = (puData[0] & 1);
00607         if ( pObj->fPhase )
00608             for ( k = 0; k < nWords; k++ )
00609                 puData[k] = ~puData[k];
00610     }
00611 }

Abc_ManRes_t * Abc_ManResubStart ( int  nLeavesMax,
int  nDivsMax 
) [static]

Function*************************************************************

Synopsis []

Description []

SideEffects []

SeeAlso []

Definition at line 287 of file abcResub.c.

00288 {
00289     Abc_ManRes_t * p;
00290     unsigned * pData;
00291     int i, k;
00292     assert( sizeof(unsigned) == 4 );
00293     p = ALLOC( Abc_ManRes_t, 1 );
00294     memset( p, 0, sizeof(Abc_ManRes_t) );
00295     p->nLeavesMax = nLeavesMax;
00296     p->nDivsMax   = nDivsMax;
00297     p->vDivs      = Vec_PtrAlloc( p->nDivsMax );
00298     // allocate simulation info
00299     p->nBits      = (1 << p->nLeavesMax);
00300     p->nWords     = (p->nBits <= 32)? 1 : (p->nBits / 32);
00301     p->pInfo      = ALLOC( unsigned, p->nWords * (p->nDivsMax + 1) );
00302     memset( p->pInfo, 0, sizeof(unsigned) * p->nWords * p->nLeavesMax );
00303     p->vSims      = Vec_PtrAlloc( p->nDivsMax );
00304     for ( i = 0; i < p->nDivsMax; i++ )
00305         Vec_PtrPush( p->vSims, p->pInfo + i * p->nWords );
00306     // assign the care set
00307     p->pCareSet  = p->pInfo + p->nDivsMax * p->nWords;
00308     Abc_InfoFill( p->pCareSet, p->nWords );
00309     // set elementary truth tables
00310     for ( k = 0; k < p->nLeavesMax; k++ )
00311     {
00312         pData = p->vSims->pArray[k];
00313         for ( i = 0; i < p->nBits; i++ )
00314             if ( i & (1 << k) )
00315                 pData[i>>5] |= (1 << (i&31));
00316     }
00317     // create the remaining divisors
00318     p->vDivs1UP  = Vec_PtrAlloc( p->nDivsMax );
00319     p->vDivs1UN  = Vec_PtrAlloc( p->nDivsMax );
00320     p->vDivs1B   = Vec_PtrAlloc( p->nDivsMax );
00321     p->vDivs2UP0 = Vec_PtrAlloc( p->nDivsMax );
00322     p->vDivs2UP1 = Vec_PtrAlloc( p->nDivsMax );
00323     p->vDivs2UN0 = Vec_PtrAlloc( p->nDivsMax );
00324     p->vDivs2UN1 = Vec_PtrAlloc( p->nDivsMax );
00325     p->vTemp     = Vec_PtrAlloc( p->nDivsMax );
00326     return p;
00327 }

void Abc_ManResubStop ( Abc_ManRes_t *  p  )  [static]

Function*************************************************************

Synopsis []

Description []

SideEffects []

SeeAlso []

Definition at line 340 of file abcResub.c.

00341 {
00342     Vec_PtrFree( p->vDivs );
00343     Vec_PtrFree( p->vSims );
00344     Vec_PtrFree( p->vDivs1UP );
00345     Vec_PtrFree( p->vDivs1UN );
00346     Vec_PtrFree( p->vDivs1B );
00347     Vec_PtrFree( p->vDivs2UP0 );
00348     Vec_PtrFree( p->vDivs2UP1 );
00349     Vec_PtrFree( p->vDivs2UN0 );
00350     Vec_PtrFree( p->vDivs2UN1 );
00351     Vec_PtrFree( p->vTemp );
00352     free( p->pInfo );
00353     free( p );
00354 }

void* Abc_NtkDontCareAlloc ( int  nVarsMax,
int  nLevels,
int  fVerbose,
int  fVeryVerbose 
)

FUNCTION DEFINITIONS ///Function*************************************************************

Synopsis [Allocates the don't-care manager.]

Description [The parameters are the max number of cut variables, the number of fanout levels used for the ODC computation, and verbosiness.]

SideEffects []

SeeAlso []

Definition at line 166 of file abcOdc.c.

00167 {
00168     Odc_Man_t * p;
00169     unsigned * pData;
00170     int i, k;
00171     p = ALLOC( Odc_Man_t, 1 );
00172     memset( p, 0, sizeof(Odc_Man_t) );
00173     assert( nVarsMax > 4 && nVarsMax < 16 );
00174     assert( nLevels > 0 && nLevels < 10 );
00175 
00176     srand( 0xABC );
00177 
00178     // dont'-care parameters
00179     p->nVarsMax     = nVarsMax;
00180     p->nLevels      = nLevels;
00181     p->fVerbose     = fVerbose;
00182     p->fVeryVerbose = fVeryVerbose;
00183     p->nPercCutoff  = 10;
00184 
00185     // windowing
00186     p->vRoots    = Vec_PtrAlloc( 128 );
00187     p->vBranches = Vec_PtrAlloc( 128 );
00188 
00189     // internal AIG package
00190     // allocate room for objects
00191     p->nObjsAlloc = ABC_DC_MAX_NODES; 
00192     p->pObjs = ALLOC( Odc_Obj_t, p->nObjsAlloc * sizeof(Odc_Obj_t) );
00193     p->nPis  = nVarsMax + 32;
00194     p->nObjs = 1 + p->nPis;
00195     memset( p->pObjs, 0, p->nObjs * sizeof(Odc_Obj_t) );
00196     // set the PI masks
00197     for ( i = 0; i < 32; i++ )
00198         p->pObjs[1 + p->nVarsMax + i].uMask = (1 << i);
00199     // allocate hash table
00200     p->nTableSize = p->nObjsAlloc/3 + 1;
00201     p->pTable = ALLOC( Odc_Lit_t, p->nTableSize * sizeof(Odc_Lit_t) );
00202     memset( p->pTable, 0, p->nTableSize * sizeof(Odc_Lit_t) );
00203     p->vUsedSpots = Vec_IntAlloc( 1000 );
00204 
00205     // truth tables
00206     p->nWords = Abc_TruthWordNum( p->nVarsMax );
00207     p->nBits = p->nWords * 8 * sizeof(unsigned);
00208     p->vTruths = Vec_PtrAllocSimInfo( p->nObjsAlloc, p->nWords );
00209     p->vTruthsElem = Vec_PtrAllocSimInfo( p->nVarsMax, p->nWords );
00210 
00211     // set elementary truth tables
00212     Abc_InfoFill( Vec_PtrEntry(p->vTruths, 0), p->nWords );
00213     for ( k = 0; k < p->nVarsMax; k++ )
00214     {
00215 //        pData = Odc_ObjTruth( p, Odc_Var(p, k) );
00216         pData = Vec_PtrEntry( p->vTruthsElem, k );
00217         Abc_InfoClear( pData, p->nWords );
00218         for ( i = 0; i < p->nBits; i++ )
00219             if ( i & (1 << k) )
00220                 pData[i>>5] |= (1 << (i&31));
00221     }
00222 
00223     // set random truth table for the additional inputs
00224     for ( k = p->nVarsMax; k < p->nPis; k++ )
00225     {
00226         pData = Odc_ObjTruth( p, Odc_Var(p, k) );
00227         Abc_InfoRandom( pData, p->nWords );
00228     }
00229 
00230     // set the miter to the unused value
00231     p->iRoot = 0xffff;
00232     return p;
00233 }

void Abc_NtkDontCareClear ( void *  p  ) 
int Abc_NtkDontCareCompute ( void *  p,
Abc_Obj_t *  pNode,
Vec_Ptr_t *  vLeaves,
unsigned *  puTruth 
)
void Abc_NtkDontCareFree ( void *  p  ) 
int Abc_NtkResubstitute ( Abc_Ntk_t *  pNtk,
int  nCutMax,
int  nStepsMax,
int  nLevelsOdc,
bool  fUpdateLevel,
bool  fVerbose,
bool  fVeryVerbose 
)

FUNCTION DEFINITIONS ///Function*************************************************************

Synopsis [Performs incremental resynthesis of the AIG.]

Description []

SideEffects []

SeeAlso []

Definition at line 140 of file abcResub.c.

00141 {
00142     ProgressBar * pProgress;
00143     Abc_ManRes_t * pManRes;
00144     Abc_ManCut_t * pManCut;
00145     void * pManOdc = NULL;
00146     Dec_Graph_t * pFForm;
00147     Vec_Ptr_t * vLeaves;
00148     Abc_Obj_t * pNode;
00149     int clk, clkStart = clock();
00150     int i, nNodes;
00151 
00152     assert( Abc_NtkIsStrash(pNtk) );
00153 
00154     // cleanup the AIG
00155     Abc_AigCleanup(pNtk->pManFunc);
00156     // start the managers
00157     pManCut = Abc_NtkManCutStart( nCutMax, 100000, 100000, 100000 );
00158     pManRes = Abc_ManResubStart( nCutMax, ABC_RS_DIV1_MAX );
00159     if ( nLevelsOdc > 0 )
00160     pManOdc = Abc_NtkDontCareAlloc( nCutMax, nLevelsOdc, fVerbose, fVeryVerbose );
00161 
00162     // compute the reverse levels if level update is requested
00163     if ( fUpdateLevel )
00164         Abc_NtkStartReverseLevels( pNtk, 0 );
00165 
00166     if ( Abc_NtkLatchNum(pNtk) )
00167         Abc_NtkForEachLatch(pNtk, pNode, i)
00168             pNode->pNext = pNode->pData;
00169 
00170     // resynthesize each node once
00171     pManRes->nNodesBeg = Abc_NtkNodeNum(pNtk);
00172     nNodes = Abc_NtkObjNumMax(pNtk);
00173     pProgress = Extra_ProgressBarStart( stdout, nNodes );
00174     Abc_NtkForEachNode( pNtk, pNode, i )
00175     {
00176         Extra_ProgressBarUpdate( pProgress, i, NULL );
00177         // skip the constant node
00178 //        if ( Abc_NodeIsConst(pNode) )
00179 //            continue;
00180         // skip persistant nodes
00181         if ( Abc_NodeIsPersistant(pNode) )
00182             continue;
00183         // skip the nodes with many fanouts
00184         if ( Abc_ObjFanoutNum(pNode) > 1000 )
00185             continue;
00186         // stop if all nodes have been tried once
00187         if ( i >= nNodes )
00188             break;
00189 
00190         // compute a reconvergence-driven cut
00191 clk = clock();
00192         vLeaves = Abc_NodeFindCut( pManCut, pNode, 0 );
00193 //        vLeaves = Abc_CutFactorLarge( pNode, nCutMax );
00194 pManRes->timeCut += clock() - clk;
00195 /*
00196         if ( fVerbose && vLeaves )
00197         printf( "Node %6d : Leaves = %3d. Volume = %3d.\n", pNode->Id, Vec_PtrSize(vLeaves), Abc_CutVolumeCheck(pNode, vLeaves) );
00198         if ( vLeaves == NULL )
00199             continue;
00200 */
00201         // get the don't-cares
00202         if ( pManOdc )
00203         {
00204 clk = clock();
00205             Abc_NtkDontCareClear( pManOdc );
00206             Abc_NtkDontCareCompute( pManOdc, pNode, vLeaves, pManRes->pCareSet );
00207 pManRes->timeTruth += clock() - clk;
00208         }
00209 
00210         // evaluate this cut
00211 clk = clock();
00212         pFForm = Abc_ManResubEval( pManRes, pNode, vLeaves, nStepsMax, fUpdateLevel, fVerbose );
00213 //        Vec_PtrFree( vLeaves );
00214 //        Abc_ManResubCleanup( pManRes );
00215 pManRes->timeRes += clock() - clk;
00216         if ( pFForm == NULL )
00217             continue;
00218         pManRes->nTotalGain += pManRes->nLastGain;
00219 /*
00220         if ( pManRes->nLeaves == 4 && pManRes->nMffc == 2 && pManRes->nLastGain == 1 )
00221         {
00222             printf( "%6d :  L = %2d. V = %2d. Mffc = %2d. Divs = %3d.   Up = %3d. Un = %3d. B = %3d.\n", 
00223                    pNode->Id, pManRes->nLeaves, Abc_CutVolumeCheck(pNode, vLeaves), pManRes->nMffc, pManRes->nDivs, 
00224                    pManRes->vDivs1UP->nSize, pManRes->vDivs1UN->nSize, pManRes->vDivs1B->nSize );
00225             Abc_ManResubPrintDivs( pManRes, pNode, vLeaves );
00226         }
00227 */
00228         // acceptable replacement found, update the graph
00229 clk = clock();
00230         Dec_GraphUpdateNetwork( pNode, pFForm, fUpdateLevel, pManRes->nLastGain );
00231 pManRes->timeNtk += clock() - clk;
00232         Dec_GraphFree( pFForm );
00233     }
00234     Extra_ProgressBarStop( pProgress );
00235 pManRes->timeTotal = clock() - clkStart;
00236     pManRes->nNodesEnd = Abc_NtkNodeNum(pNtk);
00237 
00238     // print statistics
00239     if ( fVerbose )
00240     Abc_ManResubPrint( pManRes );
00241 
00242     // delete the managers
00243     Abc_ManResubStop( pManRes );
00244     Abc_NtkManCutStop( pManCut );
00245     if ( pManOdc ) Abc_NtkDontCareFree( pManOdc );
00246 
00247     // clean the data field
00248     Abc_NtkForEachObj( pNtk, pNode, i )
00249         pNode->pData = NULL;
00250 
00251     if ( Abc_NtkLatchNum(pNtk) )
00252         Abc_NtkForEachLatch(pNtk, pNode, i)
00253             pNode->pData = pNode->pNext, pNode->pNext = NULL;
00254 
00255     // put the nodes into the DFS order and reassign their IDs
00256     Abc_NtkReassignIds( pNtk );
00257 //    Abc_AigCheckFaninOrder( pNtk->pManFunc );
00258     // fix the levels
00259     if ( fUpdateLevel )
00260         Abc_NtkStopReverseLevels( pNtk );
00261     else
00262         Abc_NtkLevel( pNtk );
00263     // check
00264     if ( !Abc_NtkCheck( pNtk ) )
00265     {
00266         printf( "Abc_NtkRefactor: The network check has failed.\n" );
00267         return 0;
00268     }
00269 s_ResubTime = clock() - clkStart;
00270     return 1;
00271 }

Variable Documentation

int s_ResubTime

Definition at line 36 of file abcPrint.c.

Generated on Tue Jan 5 12:18:41 2010 for abc70930 by  doxygen 1.6.1