src/cuBdd/cuddMatMult.c File Reference
#include "util.h"#include "cuddInt.h"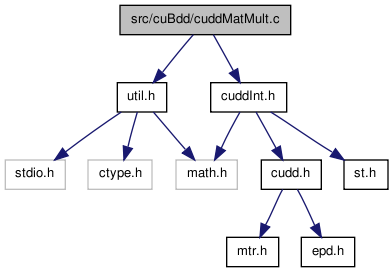
Go to the source code of this file.
Functions | |
| static DdNode * | addMMRecur (DdManager *dd, DdNode *A, DdNode *B, int topP, int *vars) |
| static DdNode * | addTriangleRecur (DdManager *dd, DdNode *f, DdNode *g, int *vars, DdNode *cube) |
| static DdNode * | cuddAddOuterSumRecur (DdManager *dd, DdNode *M, DdNode *r, DdNode *c) |
| DdNode * | Cudd_addMatrixMultiply (DdManager *dd, DdNode *A, DdNode *B, DdNode **z, int nz) |
| DdNode * | Cudd_addTimesPlus (DdManager *dd, DdNode *A, DdNode *B, DdNode **z, int nz) |
| DdNode * | Cudd_addTriangle (DdManager *dd, DdNode *f, DdNode *g, DdNode **z, int nz) |
| DdNode * | Cudd_addOuterSum (DdManager *dd, DdNode *M, DdNode *r, DdNode *c) |
Variables | |
| static char rcsid[] | DD_UNUSED = "$Id: cuddMatMult.c,v 1.17 2004/08/13 18:04:50 fabio Exp $" |
Function Documentation
| static DdNode * addMMRecur | ( | DdManager * | dd, | |
| DdNode * | A, | |||
| DdNode * | B, | |||
| int | topP, | |||
| int * | vars | |||
| ) | [static] |
AutomaticStart
Function********************************************************************
Synopsis [Performs the recursive step of Cudd_addMatrixMultiply.]
Description [Performs the recursive step of Cudd_addMatrixMultiply. Returns a pointer to the result if successful; NULL otherwise.]
SideEffects [None]
Definition at line 329 of file cuddMatMult.c.
00335 { 00336 DdNode *zero, 00337 *At, /* positive cofactor of first operand */ 00338 *Ae, /* negative cofactor of first operand */ 00339 *Bt, /* positive cofactor of second operand */ 00340 *Be, /* negative cofactor of second operand */ 00341 *t, /* positive cofactor of result */ 00342 *e, /* negative cofactor of result */ 00343 *scaled, /* scaled result */ 00344 *add_scale, /* ADD representing the scaling factor */ 00345 *res; 00346 int i; /* loop index */ 00347 double scale; /* scaling factor */ 00348 int index; /* index of the top variable */ 00349 CUDD_VALUE_TYPE value; 00350 unsigned int topA, topB, topV; 00351 DD_CTFP cacheOp; 00352 00353 statLine(dd); 00354 zero = DD_ZERO(dd); 00355 00356 if (A == zero || B == zero) { 00357 return(zero); 00358 } 00359 00360 if (cuddIsConstant(A) && cuddIsConstant(B)) { 00361 /* Compute the scaling factor. It is 2^k, where k is the 00362 ** number of summation variables below the current variable. 00363 ** Indeed, these constants represent blocks of 2^k identical 00364 ** constant values in both A and B. 00365 */ 00366 value = cuddV(A) * cuddV(B); 00367 for (i = 0; i < dd->size; i++) { 00368 if (vars[i]) { 00369 if (dd->perm[i] > topP) { 00370 value *= (CUDD_VALUE_TYPE) 2; 00371 } 00372 } 00373 } 00374 res = cuddUniqueConst(dd, value); 00375 return(res); 00376 } 00377 00378 /* Standardize to increase cache efficiency. Clearly, A*B != B*A 00379 ** in matrix multiplication. However, which matrix is which is 00380 ** determined by the variables appearing in the ADDs and not by 00381 ** which one is passed as first argument. 00382 */ 00383 if (A > B) { 00384 DdNode *tmp = A; 00385 A = B; 00386 B = tmp; 00387 } 00388 00389 topA = cuddI(dd,A->index); topB = cuddI(dd,B->index); 00390 topV = ddMin(topA,topB); 00391 00392 cacheOp = (DD_CTFP) addMMRecur; 00393 res = cuddCacheLookup2(dd,cacheOp,A,B); 00394 if (res != NULL) { 00395 /* If the result is 0, there is no need to normalize. 00396 ** Otherwise we count the number of z variables between 00397 ** the current depth and the top of the ADDs. These are 00398 ** the missing variables that determine the size of the 00399 ** constant blocks. 00400 */ 00401 if (res == zero) return(res); 00402 scale = 1.0; 00403 for (i = 0; i < dd->size; i++) { 00404 if (vars[i]) { 00405 if (dd->perm[i] > topP && (unsigned) dd->perm[i] < topV) { 00406 scale *= 2; 00407 } 00408 } 00409 } 00410 if (scale > 1.0) { 00411 cuddRef(res); 00412 add_scale = cuddUniqueConst(dd,(CUDD_VALUE_TYPE)scale); 00413 if (add_scale == NULL) { 00414 Cudd_RecursiveDeref(dd, res); 00415 return(NULL); 00416 } 00417 cuddRef(add_scale); 00418 scaled = cuddAddApplyRecur(dd,Cudd_addTimes,res,add_scale); 00419 if (scaled == NULL) { 00420 Cudd_RecursiveDeref(dd, add_scale); 00421 Cudd_RecursiveDeref(dd, res); 00422 return(NULL); 00423 } 00424 cuddRef(scaled); 00425 Cudd_RecursiveDeref(dd, add_scale); 00426 Cudd_RecursiveDeref(dd, res); 00427 res = scaled; 00428 cuddDeref(res); 00429 } 00430 return(res); 00431 } 00432 00433 /* compute the cofactors */ 00434 if (topV == topA) { 00435 At = cuddT(A); 00436 Ae = cuddE(A); 00437 } else { 00438 At = Ae = A; 00439 } 00440 if (topV == topB) { 00441 Bt = cuddT(B); 00442 Be = cuddE(B); 00443 } else { 00444 Bt = Be = B; 00445 } 00446 00447 t = addMMRecur(dd, At, Bt, (int)topV, vars); 00448 if (t == NULL) return(NULL); 00449 cuddRef(t); 00450 e = addMMRecur(dd, Ae, Be, (int)topV, vars); 00451 if (e == NULL) { 00452 Cudd_RecursiveDeref(dd, t); 00453 return(NULL); 00454 } 00455 cuddRef(e); 00456 00457 index = dd->invperm[topV]; 00458 if (vars[index] == 0) { 00459 /* We have split on either the rows of A or the columns 00460 ** of B. We just need to connect the two subresults, 00461 ** which correspond to two submatrices of the result. 00462 */ 00463 res = (t == e) ? t : cuddUniqueInter(dd,index,t,e); 00464 if (res == NULL) { 00465 Cudd_RecursiveDeref(dd, t); 00466 Cudd_RecursiveDeref(dd, e); 00467 return(NULL); 00468 } 00469 cuddRef(res); 00470 cuddDeref(t); 00471 cuddDeref(e); 00472 } else { 00473 /* we have simultaneously split on the columns of A and 00474 ** the rows of B. The two subresults must be added. 00475 */ 00476 res = cuddAddApplyRecur(dd,Cudd_addPlus,t,e); 00477 if (res == NULL) { 00478 Cudd_RecursiveDeref(dd, t); 00479 Cudd_RecursiveDeref(dd, e); 00480 return(NULL); 00481 } 00482 cuddRef(res); 00483 Cudd_RecursiveDeref(dd, t); 00484 Cudd_RecursiveDeref(dd, e); 00485 } 00486 00487 cuddCacheInsert2(dd,cacheOp,A,B,res); 00488 00489 /* We have computed (and stored in the computed table) a minimal 00490 ** result; that is, a result that assumes no summation variables 00491 ** between the current depth of the recursion and its top 00492 ** variable. We now take into account the z variables by properly 00493 ** scaling the result. 00494 */ 00495 if (res != zero) { 00496 scale = 1.0; 00497 for (i = 0; i < dd->size; i++) { 00498 if (vars[i]) { 00499 if (dd->perm[i] > topP && (unsigned) dd->perm[i] < topV) { 00500 scale *= 2; 00501 } 00502 } 00503 } 00504 if (scale > 1.0) { 00505 add_scale = cuddUniqueConst(dd,(CUDD_VALUE_TYPE)scale); 00506 if (add_scale == NULL) { 00507 Cudd_RecursiveDeref(dd, res); 00508 return(NULL); 00509 } 00510 cuddRef(add_scale); 00511 scaled = cuddAddApplyRecur(dd,Cudd_addTimes,res,add_scale); 00512 if (scaled == NULL) { 00513 Cudd_RecursiveDeref(dd, res); 00514 Cudd_RecursiveDeref(dd, add_scale); 00515 return(NULL); 00516 } 00517 cuddRef(scaled); 00518 Cudd_RecursiveDeref(dd, add_scale); 00519 Cudd_RecursiveDeref(dd, res); 00520 res = scaled; 00521 } 00522 } 00523 cuddDeref(res); 00524 return(res); 00525 00526 } /* end of addMMRecur */
| static DdNode * addTriangleRecur | ( | DdManager * | dd, | |
| DdNode * | f, | |||
| DdNode * | g, | |||
| int * | vars, | |||
| DdNode * | cube | |||
| ) | [static] |
Function********************************************************************
Synopsis [Performs the recursive step of Cudd_addTriangle.]
Description [Performs the recursive step of Cudd_addTriangle. Returns a pointer to the result if successful; NULL otherwise.]
SideEffects [None]
Definition at line 540 of file cuddMatMult.c.
00546 { 00547 DdNode *fv, *fvn, *gv, *gvn, *t, *e, *res; 00548 CUDD_VALUE_TYPE value; 00549 int top, topf, topg, index; 00550 00551 statLine(dd); 00552 if (f == DD_PLUS_INFINITY(dd) || g == DD_PLUS_INFINITY(dd)) { 00553 return(DD_PLUS_INFINITY(dd)); 00554 } 00555 00556 if (cuddIsConstant(f) && cuddIsConstant(g)) { 00557 value = cuddV(f) + cuddV(g); 00558 res = cuddUniqueConst(dd, value); 00559 return(res); 00560 } 00561 if (f < g) { 00562 DdNode *tmp = f; 00563 f = g; 00564 g = tmp; 00565 } 00566 00567 if (f->ref != 1 || g->ref != 1) { 00568 res = cuddCacheLookup(dd, DD_ADD_TRIANGLE_TAG, f, g, cube); 00569 if (res != NULL) { 00570 return(res); 00571 } 00572 } 00573 00574 topf = cuddI(dd,f->index); topg = cuddI(dd,g->index); 00575 top = ddMin(topf,topg); 00576 00577 if (top == topf) {fv = cuddT(f); fvn = cuddE(f);} else {fv = fvn = f;} 00578 if (top == topg) {gv = cuddT(g); gvn = cuddE(g);} else {gv = gvn = g;} 00579 00580 t = addTriangleRecur(dd, fv, gv, vars, cube); 00581 if (t == NULL) return(NULL); 00582 cuddRef(t); 00583 e = addTriangleRecur(dd, fvn, gvn, vars, cube); 00584 if (e == NULL) { 00585 Cudd_RecursiveDeref(dd, t); 00586 return(NULL); 00587 } 00588 cuddRef(e); 00589 00590 index = dd->invperm[top]; 00591 if (vars[index] < 0) { 00592 res = (t == e) ? t : cuddUniqueInter(dd,index,t,e); 00593 if (res == NULL) { 00594 Cudd_RecursiveDeref(dd, t); 00595 Cudd_RecursiveDeref(dd, e); 00596 return(NULL); 00597 } 00598 cuddDeref(t); 00599 cuddDeref(e); 00600 } else { 00601 res = cuddAddApplyRecur(dd,Cudd_addMinimum,t,e); 00602 if (res == NULL) { 00603 Cudd_RecursiveDeref(dd, t); 00604 Cudd_RecursiveDeref(dd, e); 00605 return(NULL); 00606 } 00607 cuddRef(res); 00608 Cudd_RecursiveDeref(dd, t); 00609 Cudd_RecursiveDeref(dd, e); 00610 cuddDeref(res); 00611 } 00612 00613 if (f->ref != 1 || g->ref != 1) { 00614 cuddCacheInsert(dd, DD_ADD_TRIANGLE_TAG, f, g, cube, res); 00615 } 00616 00617 return(res); 00618 00619 } /* end of addTriangleRecur */
AutomaticEnd Function********************************************************************
Synopsis [Calculates the product of two matrices represented as ADDs.]
Description [Calculates the product of two matrices, A and B, represented as ADDs. This procedure implements the quasiring multiplication algorithm. A is assumed to depend on variables x (rows) and z (columns). B is assumed to depend on variables z (rows) and y (columns). The product of A and B then depends on x (rows) and y (columns). Only the z variables have to be explicitly identified; they are the "summation" variables. Returns a pointer to the result if successful; NULL otherwise.]
SideEffects [None]
SeeAlso [Cudd_addTimesPlus Cudd_addTriangle Cudd_bddAndAbstract]
Definition at line 128 of file cuddMatMult.c.
00134 { 00135 int i, nvars, *vars; 00136 DdNode *res; 00137 00138 /* Array vars says what variables are "summation" variables. */ 00139 nvars = dd->size; 00140 vars = ALLOC(int,nvars); 00141 if (vars == NULL) { 00142 dd->errorCode = CUDD_MEMORY_OUT; 00143 return(NULL); 00144 } 00145 for (i = 0; i < nvars; i++) { 00146 vars[i] = 0; 00147 } 00148 for (i = 0; i < nz; i++) { 00149 vars[z[i]->index] = 1; 00150 } 00151 00152 do { 00153 dd->reordered = 0; 00154 res = addMMRecur(dd,A,B,-1,vars); 00155 } while (dd->reordered == 1); 00156 FREE(vars); 00157 return(res); 00158 00159 } /* end of Cudd_addMatrixMultiply */
Function********************************************************************
Synopsis [Takes the minimum of a matrix and the outer sum of two vectors.]
Description [Takes the pointwise minimum of a matrix and the outer sum of two vectors. This procedure is used in the Floyd-Warshall all-pair shortest path algorithm. Returns a pointer to the result if successful; NULL otherwise.]
SideEffects [None]
SeeAlso []
Definition at line 292 of file cuddMatMult.c.
00297 { 00298 DdNode *res; 00299 00300 do { 00301 dd->reordered = 0; 00302 res = cuddAddOuterSumRecur(dd, M, r, c); 00303 } while (dd->reordered == 1); 00304 return(res); 00305 00306 } /* end of Cudd_addOuterSum */
Function********************************************************************
Synopsis [Calculates the product of two matrices represented as ADDs.]
Description [Calculates the product of two matrices, A and B, represented as ADDs, using the CMU matrix by matrix multiplication procedure by Clarke et al.. Matrix A has x's as row variables and z's as column variables, while matrix B has z's as row variables and y's as column variables. Returns the pointer to the result if successful; NULL otherwise. The resulting matrix has x's as row variables and y's as column variables.]
SideEffects [None]
SeeAlso [Cudd_addMatrixMultiply]
Definition at line 181 of file cuddMatMult.c.
00187 { 00188 DdNode *w, *cube, *tmp, *res; 00189 int i; 00190 tmp = Cudd_addApply(dd,Cudd_addTimes,A,B); 00191 if (tmp == NULL) return(NULL); 00192 Cudd_Ref(tmp); 00193 Cudd_Ref(cube = DD_ONE(dd)); 00194 for (i = nz-1; i >= 0; i--) { 00195 w = Cudd_addIte(dd,z[i],cube,DD_ZERO(dd)); 00196 if (w == NULL) { 00197 Cudd_RecursiveDeref(dd,tmp); 00198 return(NULL); 00199 } 00200 Cudd_Ref(w); 00201 Cudd_RecursiveDeref(dd,cube); 00202 cube = w; 00203 } 00204 res = Cudd_addExistAbstract(dd,tmp,cube); 00205 if (res == NULL) { 00206 Cudd_RecursiveDeref(dd,tmp); 00207 Cudd_RecursiveDeref(dd,cube); 00208 return(NULL); 00209 } 00210 Cudd_Ref(res); 00211 Cudd_RecursiveDeref(dd,cube); 00212 Cudd_RecursiveDeref(dd,tmp); 00213 Cudd_Deref(res); 00214 return(res); 00215 00216 } /* end of Cudd_addTimesPlus */
Function********************************************************************
Synopsis [Performs the triangulation step for the shortest path computation.]
Description [Implements the semiring multiplication algorithm used in the triangulation step for the shortest path computation. f is assumed to depend on variables x (rows) and z (columns). g is assumed to depend on variables z (rows) and y (columns). The product of f and g then depends on x (rows) and y (columns). Only the z variables have to be explicitly identified; they are the "abstraction" variables. Returns a pointer to the result if successful; NULL otherwise. ]
SideEffects [None]
SeeAlso [Cudd_addMatrixMultiply Cudd_bddAndAbstract]
Definition at line 239 of file cuddMatMult.c.
00245 { 00246 int i, nvars, *vars; 00247 DdNode *res, *cube; 00248 00249 nvars = dd->size; 00250 vars = ALLOC(int, nvars); 00251 if (vars == NULL) { 00252 dd->errorCode = CUDD_MEMORY_OUT; 00253 return(NULL); 00254 } 00255 for (i = 0; i < nvars; i++) vars[i] = -1; 00256 for (i = 0; i < nz; i++) vars[z[i]->index] = i; 00257 cube = Cudd_addComputeCube(dd, z, NULL, nz); 00258 if (cube == NULL) { 00259 FREE(vars); 00260 return(NULL); 00261 } 00262 cuddRef(cube); 00263 00264 do { 00265 dd->reordered = 0; 00266 res = addTriangleRecur(dd, f, g, vars, cube); 00267 } while (dd->reordered == 1); 00268 if (res != NULL) cuddRef(res); 00269 Cudd_RecursiveDeref(dd,cube); 00270 if (res != NULL) cuddDeref(res); 00271 FREE(vars); 00272 return(res); 00273 00274 } /* end of Cudd_addTriangle */
| static DdNode * cuddAddOuterSumRecur | ( | DdManager * | dd, | |
| DdNode * | M, | |||
| DdNode * | r, | |||
| DdNode * | c | |||
| ) | [static] |
Function********************************************************************
Synopsis [Performs the recursive step of Cudd_addOuterSum.]
Description [Performs the recursive step of Cudd_addOuterSum. Returns a pointer to the result if successful; NULL otherwise.]
SideEffects [None]
SeeAlso []
Definition at line 635 of file cuddMatMult.c.
00640 { 00641 DdNode *P, *R, *Mt, *Me, *rt, *re, *ct, *ce, *Rt, *Re; 00642 int topM, topc, topr; 00643 int v, index; 00644 00645 statLine(dd); 00646 /* Check special cases. */ 00647 if (r == DD_PLUS_INFINITY(dd) || c == DD_PLUS_INFINITY(dd)) return(M); 00648 00649 if (cuddIsConstant(c) && cuddIsConstant(r)) { 00650 R = cuddUniqueConst(dd,Cudd_V(c)+Cudd_V(r)); 00651 cuddRef(R); 00652 if (cuddIsConstant(M)) { 00653 if (cuddV(R) <= cuddV(M)) { 00654 cuddDeref(R); 00655 return(R); 00656 } else { 00657 Cudd_RecursiveDeref(dd,R); 00658 return(M); 00659 } 00660 } else { 00661 P = Cudd_addApply(dd,Cudd_addMinimum,R,M); 00662 cuddRef(P); 00663 Cudd_RecursiveDeref(dd,R); 00664 cuddDeref(P); 00665 return(P); 00666 } 00667 } 00668 00669 /* Check the cache. */ 00670 R = cuddCacheLookup(dd,DD_ADD_OUT_SUM_TAG,M,r,c); 00671 if (R != NULL) return(R); 00672 00673 topM = cuddI(dd,M->index); topr = cuddI(dd,r->index); 00674 topc = cuddI(dd,c->index); 00675 v = ddMin(topM,ddMin(topr,topc)); 00676 00677 /* Compute cofactors. */ 00678 if (topM == v) { Mt = cuddT(M); Me = cuddE(M); } else { Mt = Me = M; } 00679 if (topr == v) { rt = cuddT(r); re = cuddE(r); } else { rt = re = r; } 00680 if (topc == v) { ct = cuddT(c); ce = cuddE(c); } else { ct = ce = c; } 00681 00682 /* Recursively solve. */ 00683 Rt = cuddAddOuterSumRecur(dd,Mt,rt,ct); 00684 if (Rt == NULL) return(NULL); 00685 cuddRef(Rt); 00686 Re = cuddAddOuterSumRecur(dd,Me,re,ce); 00687 if (Re == NULL) { 00688 Cudd_RecursiveDeref(dd, Rt); 00689 return(NULL); 00690 } 00691 cuddRef(Re); 00692 index = dd->invperm[v]; 00693 R = (Rt == Re) ? Rt : cuddUniqueInter(dd,index,Rt,Re); 00694 if (R == NULL) { 00695 Cudd_RecursiveDeref(dd, Rt); 00696 Cudd_RecursiveDeref(dd, Re); 00697 return(NULL); 00698 } 00699 cuddDeref(Rt); 00700 cuddDeref(Re); 00701 00702 /* Store the result in the cache. */ 00703 cuddCacheInsert(dd,DD_ADD_OUT_SUM_TAG,M,r,c,R); 00704 00705 return(R); 00706 00707 } /* end of cuddAddOuterSumRecur */
Variable Documentation
char rcsid [] DD_UNUSED = "$Id: cuddMatMult.c,v 1.17 2004/08/13 18:04:50 fabio Exp $" [static] |
CFile***********************************************************************
FileName [cuddMatMult.c]
PackageName [cudd]
Synopsis [Matrix multiplication functions.]
Description [External procedures included in this module:
Static procedures included in this module:
]
Author [Fabio Somenzi]
Copyright [Copyright (c) 1995-2004, Regents of the University of Colorado
All rights reserved.
Redistribution and use in source and binary forms, with or without modification, are permitted provided that the following conditions are met:
Redistributions of source code must retain the above copyright notice, this list of conditions and the following disclaimer.
Redistributions in binary form must reproduce the above copyright notice, this list of conditions and the following disclaimer in the documentation and/or other materials provided with the distribution.
Neither the name of the University of Colorado nor the names of its contributors may be used to endorse or promote products derived from this software without specific prior written permission.
THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.]
Definition at line 83 of file cuddMatMult.c.
 1.6.1
1.6.1