src/cuBdd/cuddSat.c File Reference

#include "util.h"
#include "cuddInt.h"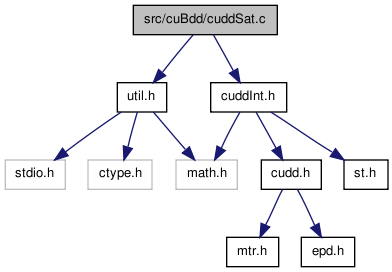

Include dependency graph for cuddSat.c:

Go to the source code of this file.

Data Structures
struct	cuddPathPair
Defines
#define	DD_BIGGY   1000000
#define	WEIGHT(weight, col)   ((weight) == NULL ? 1 : weight[col])
Functions
static enum st_retval	freePathPair (char *key, char *value, char *arg)
static cuddPathPair	getShortest (DdNode *root, int *cost, int *support, st_table *visited)
static DdNode *	getPath (DdManager *manager, st_table *visited, DdNode *f, int *weight, int cost)
static cuddPathPair	getLargest (DdNode *root, st_table *visited)
static DdNode *	getCube (DdManager *manager, st_table *visited, DdNode *f, int cost)
DdNode *	Cudd_Eval (DdManager *dd, DdNode *f, int *inputs)
DdNode *	Cudd_ShortestPath (DdManager *manager, DdNode *f, int *weight, int *support, int *length)
DdNode *	Cudd_LargestCube (DdManager *manager, DdNode *f, int *length)
int	Cudd_ShortestLength (DdManager *manager, DdNode *f, int *weight)
DdNode *	Cudd_Decreasing (DdManager *dd, DdNode *f, int i)
DdNode *	Cudd_Increasing (DdManager *dd, DdNode *f, int i)
int	Cudd_EquivDC (DdManager *dd, DdNode *F, DdNode *G, DdNode *D)
int	Cudd_bddLeqUnless (DdManager *dd, DdNode *f, DdNode *g, DdNode *D)
int	Cudd_EqualSupNorm (DdManager *dd, DdNode *f, DdNode *g, CUDD_VALUE_TYPE tolerance, int pr)
DdNode *	Cudd_bddMakePrime (DdManager *dd, DdNode *cube, DdNode *f)
DdNode *	cuddBddMakePrime (DdManager *dd, DdNode *cube, DdNode *f)
Variables
static char rcsid[]	DD_UNUSED = "$Id: cuddSat.c,v 1.36 2009/03/08 02:49:02 fabio Exp $"
static DdNode *	one
static DdNode *	zero

---

Define Documentation

#define DD_BIGGY   1000000

CFile***********************************************************************

FileName [cuddSat.c]

PackageName [cudd]

Synopsis [Functions for the solution of satisfiability related problems.]

Description [External procedures included in this file:

• Cudd_Eval()
• Cudd_ShortestPath()
• Cudd_LargestCube()
• Cudd_ShortestLength()
• Cudd_Decreasing()
• Cudd_Increasing()
• Cudd_EquivDC()
• Cudd_bddLeqUnless()
• Cudd_EqualSupNorm()
• Cudd_bddMakePrime()

Internal procedures included in this module:

• cuddBddMakePrime()

Static procedures included in this module:

• freePathPair()
• getShortest()
• getPath()
• getLargest()
• getCube()

]

Author [Seh-Woong Jeong, Fabio Somenzi]

Copyright [Copyright (c) 1995-2004, Regents of the University of Colorado

All rights reserved.

Redistribution and use in source and binary forms, with or without modification, are permitted provided that the following conditions are met:

Redistributions of source code must retain the above copyright notice, this list of conditions and the following disclaimer.

Redistributions in binary form must reproduce the above copyright notice, this list of conditions and the following disclaimer in the documentation and/or other materials provided with the distribution.

Neither the name of the University of Colorado nor the names of its contributors may be used to endorse or promote products derived from this software without specific prior written permission.

THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.]

Definition at line 79 of file cuddSat.c.

#define WEIGHT	(	weight,
		col		)	((weight) == NULL ? 1 : weight[col])

Definition at line 108 of file cuddSat.c.

---

Function Documentation

int Cudd_bddLeqUnless	(	DdManager *	dd,
		DdNode *	f,
		DdNode *	g,
		DdNode *	D
	)

Function********************************************************************

Synopsis [Tells whether f is less than of equal to G unless D is 1.]

Description [Tells whether f is less than of equal to G unless D is 1. f, g, and D are BDDs. The function returns 1 if f is less than of equal to G, and 0 otherwise. No new nodes are created.]

SideEffects [None]

SeeAlso [Cudd_EquivDC Cudd_bddLeq Cudd_bddIteConstant]

Definition at line 618 of file cuddSat.c.

{
    DdNode *tmp, *One, *F, *G;
    DdNode *Ft, *Fe, *Gt, *Ge, *Dt, *De;
    int res;
    unsigned int flevel, glevel, dlevel, top;

    statLine(dd);

    One = DD_ONE(dd);

    /* Check terminal cases. */
    if (f == g || g == One || f == Cudd_Not(One) || D == One ||
        D == f || D == Cudd_Not(g)) return(1);
    /* Check for two-operand cases. */
    if (D == Cudd_Not(One) || D == g || D == Cudd_Not(f))
        return(Cudd_bddLeq(dd,f,g));
    if (g == Cudd_Not(One) || g == Cudd_Not(f)) return(Cudd_bddLeq(dd,f,D));
    if (f == One) return(Cudd_bddLeq(dd,Cudd_Not(g),D));

    /* From now on, f, g, and D are non-constant, distinct, and
    ** non-complementary. */

    /* Normalize call to increase cache efficiency.  We rely on the
    ** fact that f <= g unless D is equivalent to not(g) <= not(f)
    ** unless D and to f <= D unless g.  We make sure that D is
    ** regular, and that at most one of f and g is complemented.  We also
    ** ensure that when two operands can be swapped, the one with the
    ** lowest address comes first. */

    if (Cudd_IsComplement(D)) {
        if (Cudd_IsComplement(g)) {
            /* Special case: if f is regular and g is complemented,
            ** f(1,...,1) = 1 > 0 = g(1,...,1).  If D(1,...,1) = 0, return 0.
            */
            if (!Cudd_IsComplement(f)) return(0);
            /* !g <= D unless !f  or  !D <= g unless !f */
            tmp = D;
            D = Cudd_Not(f);
            if (g < tmp) {
                f = Cudd_Not(g);
                g = tmp;
            } else {
                f = Cudd_Not(tmp);
            }
        } else {
            if (Cudd_IsComplement(f)) {
                /* !D <= !f unless g  or  !D <= g unless !f */
                tmp = f;
                f = Cudd_Not(D);
                if (tmp < g) {
                    D = g;
                    g = Cudd_Not(tmp);
                } else {
                    D = Cudd_Not(tmp);
                }
            } else {
                /* f <= D unless g  or  !D <= !f unless g */
                tmp = D;
                D = g;
                if (tmp < f) {
                    g = Cudd_Not(f);
                    f = Cudd_Not(tmp);
                } else {
                    g = tmp;
                }
            }
        }
    } else {
        if (Cudd_IsComplement(g)) {
            if (Cudd_IsComplement(f)) {
                /* !g <= !f unless D  or  !g <= D unless !f */
                tmp = f;
                f = Cudd_Not(g);
                if (D < tmp) {
                    g = D;
                    D = Cudd_Not(tmp);
                } else {
                    g = Cudd_Not(tmp);
                }
            } else {
                /* f <= g unless D  or  !g <= !f unless D */
                if (g < f) {
                    tmp = g;
                    g = Cudd_Not(f);
                    f = Cudd_Not(tmp);
                }
            }
        } else {
            /* f <= g unless D  or  f <= D unless g */
            if (D < g) {
                tmp = D;
                D = g;
                g = tmp;
            }
        }
    }

    /* From now on, D is regular. */

    /* Check cache. */
    tmp = cuddCacheLookup(dd,DD_BDD_LEQ_UNLESS_TAG,f,g,D);
    if (tmp != NULL) return(tmp == One);

    /* Find splitting variable. */
    F = Cudd_Regular(f);
    flevel = dd->perm[F->index];
    G = Cudd_Regular(g);
    glevel = dd->perm[G->index];
    top = ddMin(flevel,glevel);
    dlevel = dd->perm[D->index];
    top = ddMin(top,dlevel);

    /* Compute cofactors. */
    if (top == flevel) {
        Ft = cuddT(F);
        Fe = cuddE(F);
        if (F != f) {
            Ft = Cudd_Not(Ft);
            Fe = Cudd_Not(Fe);
        }
    } else {
        Ft = Fe = f;
    }
    if (top == glevel) {
        Gt = cuddT(G);
        Ge = cuddE(G);
        if (G != g) {
            Gt = Cudd_Not(Gt);
            Ge = Cudd_Not(Ge);
        }
    } else {
        Gt = Ge = g;
    }
    if (top == dlevel) {
        Dt = cuddT(D);
        De = cuddE(D);
    } else {
        Dt = De = D;
    }

    /* Solve recursively. */
    res = Cudd_bddLeqUnless(dd,Ft,Gt,Dt);
    if (res != 0) {
        res = Cudd_bddLeqUnless(dd,Fe,Ge,De);
    }
    cuddCacheInsert(dd,DD_BDD_LEQ_UNLESS_TAG,f,g,D,Cudd_NotCond(One,!res));

    return(res);

} /* end of Cudd_bddLeqUnless */

DdNode* Cudd_bddMakePrime	(	DdManager *	dd,
		DdNode *	cube,
		DdNode *	f
	)

Function********************************************************************

Synopsis [Expands cube to a prime implicant of f.]

Description [Expands cube to a prime implicant of f. Returns the prime if successful; NULL otherwise. In particular, NULL is returned if cube is not a real cube or is not an implicant of f.]

SideEffects [None]

SeeAlso []

Definition at line 860 of file cuddSat.c.

{
    DdNode *res;

    if (!Cudd_bddLeq(dd,cube,f)) return(NULL);

    do {
        dd->reordered = 0;
        res = cuddBddMakePrime(dd,cube,f);
    } while (dd->reordered == 1);
    return(res);

} /* end of Cudd_bddMakePrime */

DdNode* Cudd_Decreasing	(	DdManager *	dd,
		DdNode *	f,
		int	i
	)

Function********************************************************************

Synopsis [Determines whether a BDD is negative unate in a variable.]

Description [Determines whether the function represented by BDD f is negative unate (monotonic decreasing) in variable i. Returns the constant one is f is unate and the (logical) constant zero if it is not. This function does not generate any new nodes.]

SideEffects [None]

SeeAlso [Cudd_Increasing]

Definition at line 413 of file cuddSat.c.

{
    unsigned int topf, level;
    DdNode *F, *fv, *fvn, *res;
    DD_CTFP cacheOp;

    statLine(dd);
#ifdef DD_DEBUG
    assert(0 <= i && i < dd->size);
#endif

    F = Cudd_Regular(f);
    topf = cuddI(dd,F->index);

    /* Check terminal case. If topf > i, f does not depend on var.
    ** Therefore, f is unate in i.
    */
    level = (unsigned) dd->perm[i];
    if (topf > level) {
        return(DD_ONE(dd));
    }

    /* From now on, f is not constant. */

    /* Check cache. */
    cacheOp = (DD_CTFP) Cudd_Decreasing;
    res = cuddCacheLookup2(dd,cacheOp,f,dd->vars[i]);
    if (res != NULL) {
        return(res);
    }

    /* Compute cofactors. */
    fv = cuddT(F); fvn = cuddE(F);
    if (F != f) {
        fv = Cudd_Not(fv);
        fvn = Cudd_Not(fvn);
    }

    if (topf == (unsigned) level) {
        /* Special case: if fv is regular, fv(1,...,1) = 1;
        ** If in addition fvn is complemented, fvn(1,...,1) = 0.
        ** But then f(1,1,...,1) > f(0,1,...,1). Hence f is not
        ** monotonic decreasing in i.
        */
        if (!Cudd_IsComplement(fv) && Cudd_IsComplement(fvn)) {
            return(Cudd_Not(DD_ONE(dd)));
        }
        res = Cudd_bddLeq(dd,fv,fvn) ? DD_ONE(dd) : Cudd_Not(DD_ONE(dd));
    } else {
        res = Cudd_Decreasing(dd,fv,i);
        if (res == DD_ONE(dd)) {
            res = Cudd_Decreasing(dd,fvn,i);
        }
    }

    cuddCacheInsert2(dd,cacheOp,f,dd->vars[i],res);
    return(res);

} /* end of Cudd_Decreasing */

int Cudd_EqualSupNorm	(	DdManager *	dd,
		DdNode *	f,
		DdNode *	g,
		CUDD_VALUE_TYPE	tolerance,
		int	pr
	)

Function********************************************************************

Synopsis [Compares two ADDs for equality within tolerance.]

Description [Compares two ADDs for equality within tolerance. Two ADDs are reported to be equal if the maximum difference between them (the sup norm of their difference) is less than or equal to the tolerance parameter. Returns 1 if the two ADDs are equal (within tolerance); 0 otherwise. If parameter pr is positive the first failure is reported to the standard output.]

SideEffects [None]

SeeAlso []

Definition at line 792 of file cuddSat.c.

{
    DdNode *fv, *fvn, *gv, *gvn, *r;
    unsigned int topf, topg;

    statLine(dd);
    /* Check terminal cases. */
    if (f == g) return(1);
    if (Cudd_IsConstant(f) && Cudd_IsConstant(g)) {
        if (ddEqualVal(cuddV(f),cuddV(g),tolerance)) {
            return(1);
        } else {
            if (pr>0) {
                (void) fprintf(dd->out,"Offending nodes:\n");
                (void) fprintf(dd->out,
                               "f: address = %p\t value = %40.30f\n",
                               (void *) f, cuddV(f));
                (void) fprintf(dd->out,
                               "g: address = %p\t value = %40.30f\n",
                               (void *) g, cuddV(g));
            }
            return(0);
        }
    }

    /* We only insert the result in the cache if the comparison is
    ** successful. Therefore, if we hit we return 1. */
    r = cuddCacheLookup2(dd,(DD_CTFP)Cudd_EqualSupNorm,f,g);
    if (r != NULL) {
        return(1);
    }

    /* Compute the cofactors and solve the recursive subproblems. */
    topf = cuddI(dd,f->index);
    topg = cuddI(dd,g->index);

    if (topf <= topg) {fv = cuddT(f); fvn = cuddE(f);} else {fv = fvn = f;}
    if (topg <= topf) {gv = cuddT(g); gvn = cuddE(g);} else {gv = gvn = g;}

    if (!Cudd_EqualSupNorm(dd,fv,gv,tolerance,pr)) return(0);
    if (!Cudd_EqualSupNorm(dd,fvn,gvn,tolerance,pr)) return(0);

    cuddCacheInsert2(dd,(DD_CTFP)Cudd_EqualSupNorm,f,g,DD_ONE(dd));

    return(1);

} /* end of Cudd_EqualSupNorm */

int Cudd_EquivDC	(	DdManager *	dd,
		DdNode *	F,
		DdNode *	G,
		DdNode *	D
	)

Function********************************************************************

Synopsis [Tells whether F and G are identical wherever D is 0.]

Description [Tells whether F and G are identical wherever D is 0. F and G are either two ADDs or two BDDs. D is either a 0-1 ADD or a BDD. The function returns 1 if F and G are equivalent, and 0 otherwise. No new nodes are created.]

SideEffects [None]

SeeAlso [Cudd_bddLeqUnless]

Definition at line 518 of file cuddSat.c.

{
    DdNode *tmp, *One, *Gr, *Dr;
    DdNode *Fv, *Fvn, *Gv, *Gvn, *Dv, *Dvn;
    int res;
    unsigned int flevel, glevel, dlevel, top;

    One = DD_ONE(dd);

    statLine(dd);
    /* Check terminal cases. */
    if (D == One || F == G) return(1);
    if (D == Cudd_Not(One) || D == DD_ZERO(dd) || F == Cudd_Not(G)) return(0);

    /* From now on, D is non-constant. */

    /* Normalize call to increase cache efficiency. */
    if (F > G) {
        tmp = F;
        F = G;
        G = tmp;
    }
    if (Cudd_IsComplement(F)) {
        F = Cudd_Not(F);
        G = Cudd_Not(G);
    }

    /* From now on, F is regular. */

    /* Check cache. */
    tmp = cuddCacheLookup(dd,DD_EQUIV_DC_TAG,F,G,D);
    if (tmp != NULL) return(tmp == One);

    /* Find splitting variable. */
    flevel = cuddI(dd,F->index);
    Gr = Cudd_Regular(G);
    glevel = cuddI(dd,Gr->index);
    top = ddMin(flevel,glevel);
    Dr = Cudd_Regular(D);
    dlevel = dd->perm[Dr->index];
    top = ddMin(top,dlevel);

    /* Compute cofactors. */
    if (top == flevel) {
        Fv = cuddT(F);
        Fvn = cuddE(F);
    } else {
        Fv = Fvn = F;
    }
    if (top == glevel) {
        Gv = cuddT(Gr);
        Gvn = cuddE(Gr);
        if (G != Gr) {
            Gv = Cudd_Not(Gv);
            Gvn = Cudd_Not(Gvn);
        }
    } else {
        Gv = Gvn = G;
    }
    if (top == dlevel) {
        Dv = cuddT(Dr);
        Dvn = cuddE(Dr);
        if (D != Dr) {
            Dv = Cudd_Not(Dv);
            Dvn = Cudd_Not(Dvn);
        }
    } else {
        Dv = Dvn = D;
    }

    /* Solve recursively. */
    res = Cudd_EquivDC(dd,Fv,Gv,Dv);
    if (res != 0) {
        res = Cudd_EquivDC(dd,Fvn,Gvn,Dvn);
    }
    cuddCacheInsert(dd,DD_EQUIV_DC_TAG,F,G,D,(res) ? One : Cudd_Not(One));

    return(res);

} /* end of Cudd_EquivDC */

DdNode* Cudd_Eval	(	DdManager *	dd,
		DdNode *	f,
		int *	inputs
	)

AutomaticEnd Function********************************************************************

Synopsis [Returns the value of a DD for a given variable assignment.]

Description [Finds the value of a DD for a given variable assignment. The variable assignment is passed in an array of int's, that should specify a zero or a one for each variable in the support of the function. Returns a pointer to a constant node. No new nodes are produced.]

SideEffects [None]

SeeAlso [Cudd_bddLeq Cudd_addEvalConst]

Definition at line 153 of file cuddSat.c.

{
    int comple;
    DdNode *ptr;

    comple = Cudd_IsComplement(f);
    ptr = Cudd_Regular(f);

    while (!cuddIsConstant(ptr)) {
        if (inputs[ptr->index] == 1) {
            ptr = cuddT(ptr);
        } else {
            comple ^= Cudd_IsComplement(cuddE(ptr));
            ptr = Cudd_Regular(cuddE(ptr));
        }
    }
    return(Cudd_NotCond(ptr,comple));

} /* end of Cudd_Eval */

DdNode* Cudd_Increasing	(	DdManager *	dd,
		DdNode *	f,
		int	i
	)

Function********************************************************************

Synopsis [Determines whether a BDD is positive unate in a variable.]

Description [Determines whether the function represented by BDD f is positive unate (monotonic increasing) in variable i. It is based on Cudd_Decreasing and the fact that f is monotonic increasing in i if and only if its complement is monotonic decreasing in i.]

SideEffects [None]

SeeAlso [Cudd_Decreasing]

Definition at line 493 of file cuddSat.c.

{
    return(Cudd_Decreasing(dd,Cudd_Not(f),i));

} /* end of Cudd_Increasing */

DdNode* Cudd_LargestCube	(	DdManager *	manager,
		DdNode *	f,
		int *	length
	)

Function********************************************************************

Synopsis [Finds a largest cube in a DD.]

Description [Finds a largest cube in a DD. f is the DD we want to get the largest cube for. The problem is translated into the one of finding a shortest path in f, when both THEN and ELSE arcs are assumed to have unit length. This yields a largest cube in the disjoint cover corresponding to the DD. Therefore, it is not necessarily the largest implicant of f. Returns the largest cube as a BDD.]

SideEffects [The number of literals of the cube is returned in length.]

SeeAlso [Cudd_ShortestPath]

Definition at line 281 of file cuddSat.c.

{
    register    DdNode  *F;
    st_table    *visited;
    DdNode      *sol;
    cuddPathPair *rootPair;
    int         complement, cost;

    one = DD_ONE(manager);
    zero = DD_ZERO(manager);

    if (f == Cudd_Not(one) || f == zero) {
        *length = DD_BIGGY;
        return(Cudd_Not(one));
    }
    /* From this point on, a path exists. */

    do {
        manager->reordered = 0;

        /* Initialize visited table. */
        visited = st_init_table(st_ptrcmp, st_ptrhash);

        /* Now get the length of the shortest path(s) from f to 1. */
        (void) getLargest(f, visited);

        complement = Cudd_IsComplement(f);

        F = Cudd_Regular(f);

        if (!st_lookup(visited, F, &rootPair)) return(NULL);

        if (complement) {
          cost = rootPair->neg;
        } else {
          cost = rootPair->pos;
        }

        /* Recover an actual shortest path. */
        sol = getCube(manager,visited,f,cost);

        st_foreach(visited, freePathPair, NULL);
        st_free_table(visited);

    } while (manager->reordered == 1);

    *length = cost;
    return(sol);

} /* end of Cudd_LargestCube */

int Cudd_ShortestLength	(	DdManager *	manager,
		DdNode *	f,
		int *	weight
	)

Function********************************************************************

Synopsis [Find the length of the shortest path(s) in a DD.]

Description [Find the length of the shortest path(s) in a DD. f is the DD we want to get the shortest path for; weight\[i\] is the weight of the THEN edge coming from the node whose index is i. All ELSE edges have 0 weight. Returns the length of the shortest path(s) if such a path is found; a large number if the function is identically 0, and CUDD_OUT_OF_MEM in case of failure.]

SideEffects [None]

SeeAlso [Cudd_ShortestPath]

Definition at line 353 of file cuddSat.c.

{
    register    DdNode  *F;
    st_table    *visited;
    cuddPathPair *my_pair;
    int         complement, cost;

    one = DD_ONE(manager);
    zero = DD_ZERO(manager);

    if (f == Cudd_Not(one) || f == zero) {
        return(DD_BIGGY);
    }

    /* From this point on, a path exists. */
    /* Initialize visited table and support. */
    visited = st_init_table(st_ptrcmp, st_ptrhash);

    /* Now get the length of the shortest path(s) from f to 1. */
    (void) getShortest(f, weight, NULL, visited);

    complement = Cudd_IsComplement(f);

    F = Cudd_Regular(f);

    if (!st_lookup(visited, F, &my_pair)) return(CUDD_OUT_OF_MEM);
    
    if (complement) {
        cost = my_pair->neg;
    } else {
        cost = my_pair->pos;
    }

    st_foreach(visited, freePathPair, NULL);
    st_free_table(visited);

    return(cost);

} /* end of Cudd_ShortestLength */

DdNode* Cudd_ShortestPath	(	DdManager *	manager,
		DdNode *	f,
		int *	weight,
		int *	support,
		int *	length
	)

Function********************************************************************

Synopsis [Finds a shortest path in a DD.]

Description [Finds a shortest path in a DD. f is the DD we want to get the shortest path for; weight\[i\] is the weight of the THEN arc coming from the node whose index is i. If weight is NULL, then unit weights are assumed for all THEN arcs. All ELSE arcs have 0 weight. If non-NULL, both weight and support should point to arrays with at least as many entries as there are variables in the manager. Returns the shortest path as the BDD of a cube.]

SideEffects [support contains on return the true support of f. If support is NULL on entry, then Cudd_ShortestPath does not compute the true support info. length contains the length of the path.]

SeeAlso [Cudd_ShortestLength Cudd_LargestCube]

Definition at line 197 of file cuddSat.c.

{
    DdNode      *F;
    st_table    *visited;
    DdNode      *sol;
    cuddPathPair *rootPair;
    int         complement, cost;
    int         i;

    one = DD_ONE(manager);
    zero = DD_ZERO(manager);

    /* Initialize support. Support does not depend on variable order.
    ** Hence, it does not need to be reinitialized if reordering occurs.
    */
    if (support) {
      for (i = 0; i < manager->size; i++) {
        support[i] = 0;
      }
    }

    if (f == Cudd_Not(one) || f == zero) {
      *length = DD_BIGGY;
      return(Cudd_Not(one));
    }
    /* From this point on, a path exists. */

    do {
        manager->reordered = 0;

        /* Initialize visited table. */
        visited = st_init_table(st_ptrcmp, st_ptrhash);

        /* Now get the length of the shortest path(s) from f to 1. */
        (void) getShortest(f, weight, support, visited);

        complement = Cudd_IsComplement(f);

        F = Cudd_Regular(f);

        if (!st_lookup(visited, F, &rootPair)) return(NULL);

        if (complement) {
          cost = rootPair->neg;
        } else {
          cost = rootPair->pos;
        }

        /* Recover an actual shortest path. */
        sol = getPath(manager,visited,f,weight,cost);

        st_foreach(visited, freePathPair, NULL);
        st_free_table(visited);

    } while (manager->reordered == 1);

    *length = cost;
    return(sol);

} /* end of Cudd_ShortestPath */

DdNode* cuddBddMakePrime	(	DdManager *	dd,
		DdNode *	cube,
		DdNode *	f
	)

Function********************************************************************

Synopsis [Performs the recursive step of Cudd_bddMakePrime.]

Description [Performs the recursive step of Cudd_bddMakePrime. Returns the prime if successful; NULL otherwise.]

SideEffects [None]

SeeAlso []

Definition at line 896 of file cuddSat.c.

{
    DdNode *scan;
    DdNode *t, *e;
    DdNode *res = cube;
    DdNode *zero = Cudd_Not(DD_ONE(dd));

    Cudd_Ref(res);
    scan = cube;
    while (!Cudd_IsConstant(scan)) {
        DdNode *reg = Cudd_Regular(scan);
        DdNode *var = dd->vars[reg->index];
        DdNode *expanded = Cudd_bddExistAbstract(dd,res,var);
        if (expanded == NULL) {
            return(NULL);
        }
        Cudd_Ref(expanded);
        if (Cudd_bddLeq(dd,expanded,f)) {
            Cudd_RecursiveDeref(dd,res);
            res = expanded;
        } else {
            Cudd_RecursiveDeref(dd,expanded);
        }
        cuddGetBranches(scan,&t,&e);
        if (t == zero) {
            scan = e;
        } else if (e == zero) {
            scan = t;
        } else {
            Cudd_RecursiveDeref(dd,res);
            return(NULL);       /* cube is not a cube */
        }
    }

    if (scan == DD_ONE(dd)) {
        Cudd_Deref(res);
        return(res);
    } else {
        Cudd_RecursiveDeref(dd,res);
        return(NULL);
    }

} /* end of cuddBddMakePrime */

static enum st_retval freePathPair	(	char *	key,
		char *	value,
		char *	arg
	)			[static]

AutomaticStart

Function********************************************************************

Synopsis [Frees the entries of the visited symbol table.]

Description [Frees the entries of the visited symbol table. Returns ST_CONTINUE.]

SideEffects [None]

Definition at line 960 of file cuddSat.c.

{
    cuddPathPair *pair;

    pair = (cuddPathPair *) value;
        FREE(pair);
    return(ST_CONTINUE);

} /* end of freePathPair */

static DdNode * getCube	(	DdManager *	manager,
		st_table *	visited,
		DdNode *	f,
		int	cost
	)			[static]

Function********************************************************************

Synopsis [Build a BDD for a largest cube of f.]

Description [Build a BDD for a largest cube of f. Given the minimum length from the root, and the minimum lengths for each node (in visited), apply triangulation at each node. Of the two children of each node on a shortest path, at least one is on a shortest path. In case of ties the procedure chooses the THEN children. Returns a pointer to the cube BDD representing the path if successful; NULL otherwise.]

SideEffects [None]

SeeAlso []

Definition at line 1270 of file cuddSat.c.

{
    DdNode      *sol, *tmp;
    DdNode      *my_dd, *T, *E;
    cuddPathPair *T_pair, *E_pair;
    int         Tcost, Ecost;
    int         complement;

    my_dd = Cudd_Regular(f);
    complement = Cudd_IsComplement(f);

    sol = one;
    cuddRef(sol);

    while (!cuddIsConstant(my_dd)) {
        Tcost = cost - 1;
        Ecost = cost - 1;

        T = cuddT(my_dd);
        E = cuddE(my_dd);

        if (complement) {T = Cudd_Not(T); E = Cudd_Not(E);}

        if (!st_lookup(visited, Cudd_Regular(T), &T_pair)) return(NULL);
        if ((Cudd_IsComplement(T) && T_pair->neg == Tcost) ||
        (!Cudd_IsComplement(T) && T_pair->pos == Tcost)) {
            tmp = cuddBddAndRecur(manager,manager->vars[my_dd->index],sol);
            if (tmp == NULL) {
                Cudd_RecursiveDeref(manager,sol);
                return(NULL);
            }
            cuddRef(tmp);
            Cudd_RecursiveDeref(manager,sol);
            sol = tmp;

            complement =  Cudd_IsComplement(T);
            my_dd = Cudd_Regular(T);
            cost = Tcost;
            continue;
        }
        if (!st_lookup(visited, Cudd_Regular(E), &E_pair)) return(NULL);
        if ((Cudd_IsComplement(E) && E_pair->neg == Ecost) ||
        (!Cudd_IsComplement(E) && E_pair->pos == Ecost)) {
            tmp = cuddBddAndRecur(manager,Cudd_Not(manager->vars[my_dd->index]),sol);
            if (tmp == NULL) {
                Cudd_RecursiveDeref(manager,sol);
                return(NULL);
            }
            cuddRef(tmp);
            Cudd_RecursiveDeref(manager,sol);
            sol = tmp;
            complement = Cudd_IsComplement(E);
            my_dd = Cudd_Regular(E);
            cost = Ecost;
            continue;
        }
        (void) fprintf(manager->err,"We shouldn't be here!\n");
        manager->errorCode = CUDD_INTERNAL_ERROR;
        return(NULL);
    }

    cuddDeref(sol);
    return(sol);

} /* end of getCube */

static cuddPathPair getLargest	(	DdNode *	root,
		st_table *	visited
	)			[static]

Function********************************************************************

Synopsis [Finds the size of the largest cube(s) in a DD.]

Description [Finds the size of the largest cube(s) in a DD. This problem is translated into finding the shortest paths from a node when both THEN and ELSE arcs have unit lengths. Uses a local symbol table to store the lengths for each node. Only the lengths for the regular nodes are entered in the table, because those for the complement nodes are simply obtained by swapping the two lenghts. Returns a pair of lengths: the length of the shortest path to 1; and the length of the shortest path to 0. This is done so as to take complement arcs into account.]

SideEffects [none]

SeeAlso []

Definition at line 1182 of file cuddSat.c.

{
    cuddPathPair *my_pair, res_pair, pair_T, pair_E;
    DdNode      *my_root, *T, *E;

    my_root = Cudd_Regular(root);

    if (st_lookup(visited, my_root, &my_pair)) {
        if (Cudd_IsComplement(root)) {
            res_pair.pos = my_pair->neg;
            res_pair.neg = my_pair->pos;
        } else {
            res_pair.pos = my_pair->pos;
            res_pair.neg = my_pair->neg;
        }
        return(res_pair);
    }

    /* In the case of a BDD the following test is equivalent to
    ** testing whether the BDD is the constant 1. This formulation,
    ** however, works for ADDs as well, by assuming the usual
    ** dichotomy of 0 and != 0.
    */
    if (cuddIsConstant(my_root)) {
        if (my_root != zero) {
            res_pair.pos = 0;
            res_pair.neg = DD_BIGGY;
        } else {
            res_pair.pos = DD_BIGGY;
            res_pair.neg = 0;
        }
    } else {
        T = cuddT(my_root);
        E = cuddE(my_root);

        pair_T = getLargest(T, visited);
        pair_E = getLargest(E, visited);
        res_pair.pos = ddMin(pair_T.pos, pair_E.pos) + 1;
        res_pair.neg = ddMin(pair_T.neg, pair_E.neg) + 1;
    }

    my_pair = ALLOC(cuddPathPair, 1);
    if (my_pair == NULL) {      /* simply do not cache this result */
        if (Cudd_IsComplement(root)) {
            int tmp = res_pair.pos;
            res_pair.pos = res_pair.neg;
            res_pair.neg = tmp;
        }
        return(res_pair);
    }
    my_pair->pos = res_pair.pos;
    my_pair->neg = res_pair.neg;

    /* Caching may fail without affecting correctness. */
    st_insert(visited, (char *)my_root, (char *)my_pair);
    if (Cudd_IsComplement(root)) {
        res_pair.pos = my_pair->neg;
        res_pair.neg = my_pair->pos;
    } else {
        res_pair.pos = my_pair->pos;
        res_pair.neg = my_pair->neg;
    }
    return(res_pair);

} /* end of getLargest */

static DdNode * getPath	(	DdManager *	manager,
		st_table *	visited,
		DdNode *	f,
		int *	weight,
		int	cost
	)			[static]

Function********************************************************************

Synopsis [Build a BDD for a shortest path of f.]

Description [Build a BDD for a shortest path of f. Given the minimum length from the root, and the minimum lengths for each node (in visited), apply triangulation at each node. Of the two children of each node on a shortest path, at least one is on a shortest path. In case of ties the procedure chooses the THEN children. Returns a pointer to the cube BDD representing the path if successful; NULL otherwise.]

SideEffects [None]

SeeAlso []

Definition at line 1089 of file cuddSat.c.

{
    DdNode      *sol, *tmp;
    DdNode      *my_dd, *T, *E;
    cuddPathPair *T_pair, *E_pair;
    int         Tcost, Ecost;
    int         complement;

    my_dd = Cudd_Regular(f);
    complement = Cudd_IsComplement(f);

    sol = one;
    cuddRef(sol);

    while (!cuddIsConstant(my_dd)) {
        Tcost = cost - WEIGHT(weight, my_dd->index);
        Ecost = cost;

        T = cuddT(my_dd);
        E = cuddE(my_dd);

        if (complement) {T = Cudd_Not(T); E = Cudd_Not(E);}

        st_lookup(visited, Cudd_Regular(T), &T_pair);
        if ((Cudd_IsComplement(T) && T_pair->neg == Tcost) ||
        (!Cudd_IsComplement(T) && T_pair->pos == Tcost)) {
            tmp = cuddBddAndRecur(manager,manager->vars[my_dd->index],sol);
            if (tmp == NULL) {
                Cudd_RecursiveDeref(manager,sol);
                return(NULL);
            }
            cuddRef(tmp);
            Cudd_RecursiveDeref(manager,sol);
            sol = tmp;

            complement =  Cudd_IsComplement(T);
            my_dd = Cudd_Regular(T);
            cost = Tcost;
            continue;
        }
        st_lookup(visited, Cudd_Regular(E), &E_pair);
        if ((Cudd_IsComplement(E) && E_pair->neg == Ecost) ||
        (!Cudd_IsComplement(E) && E_pair->pos == Ecost)) {
            tmp = cuddBddAndRecur(manager,Cudd_Not(manager->vars[my_dd->index]),sol);
            if (tmp == NULL) {
                Cudd_RecursiveDeref(manager,sol);
                return(NULL);
            }
            cuddRef(tmp);
            Cudd_RecursiveDeref(manager,sol);
            sol = tmp;
            complement = Cudd_IsComplement(E);
            my_dd = Cudd_Regular(E);
            cost = Ecost;
            continue;
        }
        (void) fprintf(manager->err,"We shouldn't be here!!\n");
        manager->errorCode = CUDD_INTERNAL_ERROR;
        return(NULL);
    }

    cuddDeref(sol);
    return(sol);

} /* end of getPath */

static cuddPathPair getShortest	(	DdNode *	root,
		int *	cost,
		int *	support,
		st_table *	visited
	)			[static]

Function********************************************************************

Synopsis [Finds the length of the shortest path(s) in a DD.]

Description [Finds the length of the shortest path(s) in a DD. Uses a local symbol table to store the lengths for each node. Only the lengths for the regular nodes are entered in the table, because those for the complement nodes are simply obtained by swapping the two lenghts. Returns a pair of lengths: the length of the shortest path to 1; and the length of the shortest path to 0. This is done so as to take complement arcs into account.]

SideEffects [Accumulates the support of the DD in support.]

SeeAlso []

Definition at line 993 of file cuddSat.c.

{
    cuddPathPair *my_pair, res_pair, pair_T, pair_E;
    DdNode      *my_root, *T, *E;
    int         weight;

    my_root = Cudd_Regular(root);

    if (st_lookup(visited, my_root, &my_pair)) {
        if (Cudd_IsComplement(root)) {
            res_pair.pos = my_pair->neg;
            res_pair.neg = my_pair->pos;
        } else {
            res_pair.pos = my_pair->pos;
            res_pair.neg = my_pair->neg;
        }
        return(res_pair);
    }

    /* In the case of a BDD the following test is equivalent to
    ** testing whether the BDD is the constant 1. This formulation,
    ** however, works for ADDs as well, by assuming the usual
    ** dichotomy of 0 and != 0.
    */
    if (cuddIsConstant(my_root)) {
        if (my_root != zero) {
            res_pair.pos = 0;
            res_pair.neg = DD_BIGGY;
        } else {
            res_pair.pos = DD_BIGGY;
            res_pair.neg = 0;
        }
    } else {
        T = cuddT(my_root);
        E = cuddE(my_root);

        pair_T = getShortest(T, cost, support, visited);
        pair_E = getShortest(E, cost, support, visited);
        weight = WEIGHT(cost, my_root->index);
        res_pair.pos = ddMin(pair_T.pos+weight, pair_E.pos);
        res_pair.neg = ddMin(pair_T.neg+weight, pair_E.neg);

        /* Update support. */
        if (support != NULL) {
            support[my_root->index] = 1;
        }
    }

    my_pair = ALLOC(cuddPathPair, 1);
    if (my_pair == NULL) {
        if (Cudd_IsComplement(root)) {
            int tmp = res_pair.pos;
            res_pair.pos = res_pair.neg;
            res_pair.neg = tmp;
        }
        return(res_pair);
    }
    my_pair->pos = res_pair.pos;
    my_pair->neg = res_pair.neg;

    st_insert(visited, (char *)my_root, (char *)my_pair);
    if (Cudd_IsComplement(root)) {
        res_pair.pos = my_pair->neg;
        res_pair.neg = my_pair->pos;
    } else {
        res_pair.pos = my_pair->pos;
        res_pair.neg = my_pair->neg;
    }
    return(res_pair);

} /* end of getShortest */

---

Variable Documentation

char rcsid [] DD_UNUSED = "$Id: cuddSat.c,v 1.36 2009/03/08 02:49:02 fabio Exp $" [static]

Definition at line 99 of file cuddSat.c.

DdNode* one [static]

Definition at line 102 of file cuddSat.c.

DdNode * zero [static]

Definition at line 102 of file cuddSat.c.