src/opt/cut/cutExpand.c File Reference
#include "cutInt.h"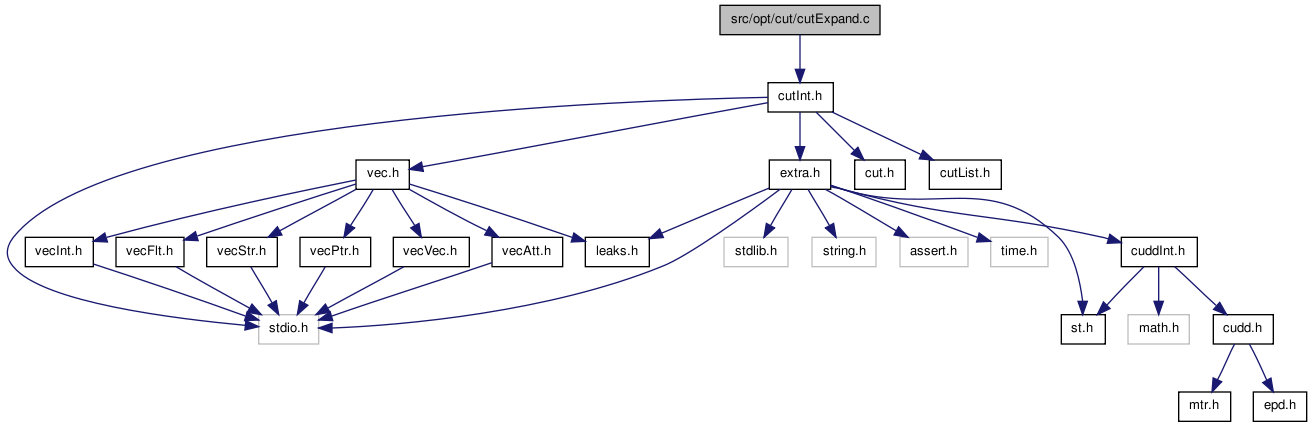
Go to the source code of this file.
Defines | |
| #define | CUT_CELL_MVAR 9 |
Functions | |
| static unsigned | Cut_TruthPhase (Cut_Cut_t *pCut, Cut_Cut_t *pCut1) |
| void | Cut_TruthCompose (Cut_Cut_t *pCutF, int Node, Cut_Cut_t *pCutT, Cut_Cut_t *pCutRes) |
Define Documentation
| #define CUT_CELL_MVAR 9 |
CFile****************************************************************
FileName [cutExpand.c]
SystemName [ABC: Logic synthesis and verification system.]
PackageName [K-feasible cut computation package.]
Synopsis [Computes the truth table of the cut after expansion.]
Author [Alan Mishchenko]
Affiliation [UC Berkeley]
Date [Ver. 1.0. Started - June 20, 2005.]
Revision [
- Id
- cutExpand.c,v 1.00 2005/06/20 00:00:00 alanmi Exp
] DECLARATIONS ///
Definition at line 27 of file cutExpand.c.
Function Documentation
Function*************************************************************
Synopsis [Computes the truth table of the composition of cuts.]
Description [Inputs are:
- a factor cut (truth table is stored inside)
- a node in the factor cut
- a tree cut to be substituted (truth table is stored inside)
- the resulting cut (truth table will be filled in). Note that all cuts, including the resulting one, should be already computed and the nodes should be stored in the ascending order.]
SideEffects []
SeeAlso []
Definition at line 78 of file cutExpand.c.
00079 { 00080 static unsigned uCof0[1<<(CUT_CELL_MVAR-5)]; 00081 static unsigned uCof1[1<<(CUT_CELL_MVAR-5)]; 00082 static unsigned uTemp[1<<(CUT_CELL_MVAR-5)]; 00083 unsigned * pIn, * pOut, * pTemp; 00084 unsigned uPhase; 00085 int NodeIndex, i, k; 00086 00087 // sanity checks 00088 assert( pCutF->nVarsMax == pCutT->nVarsMax ); 00089 assert( pCutF->nVarsMax == pCutRes->nVarsMax ); 00090 assert( pCutF->nVarsMax <= CUT_CELL_MVAR ); 00091 // the factor cut (pCutF) should have its nodes sorted in the ascending order 00092 assert( pCutF->nLeaves <= pCutF->nVarsMax ); 00093 for ( i = 0; i < (int)pCutF->nLeaves - 1; i++ ) 00094 assert( pCutF->pLeaves[i] < pCutF->pLeaves[i+1] ); 00095 // the tree cut (pCutT) should have its nodes sorted in the ascending order 00096 assert( pCutT->nLeaves <= pCutT->nVarsMax ); 00097 for ( i = 0; i < (int)pCutT->nLeaves - 1; i++ ) 00098 assert( pCutT->pLeaves[i] < pCutT->pLeaves[i+1] ); 00099 // the resulting cut (pCutRes) should have its nodes sorted in the ascending order 00100 assert( pCutRes->nLeaves <= pCutRes->nVarsMax ); 00101 for ( i = 0; i < (int)pCutRes->nLeaves - 1; i++ ) 00102 assert( pCutRes->pLeaves[i] < pCutRes->pLeaves[i+1] ); 00103 // make sure that every node in pCutF (except Node) appears in pCutRes 00104 for ( i = 0; i < (int)pCutF->nLeaves; i++ ) 00105 { 00106 if ( pCutF->pLeaves[i] == Node ) 00107 continue; 00108 for ( k = 0; k < (int)pCutRes->nLeaves; k++ ) 00109 if ( pCutF->pLeaves[i] == pCutRes->pLeaves[k] ) 00110 break; 00111 assert( k < (int)pCutRes->nLeaves ); // node i from pCutF is not found in pCutRes!!! 00112 } 00113 // make sure that every node in pCutT appears in pCutRes 00114 for ( i = 0; i < (int)pCutT->nLeaves; i++ ) 00115 { 00116 for ( k = 0; k < (int)pCutRes->nLeaves; k++ ) 00117 if ( pCutT->pLeaves[i] == pCutRes->pLeaves[k] ) 00118 break; 00119 assert( k < (int)pCutRes->nLeaves ); // node i from pCutT is not found in pCutRes!!! 00120 } 00121 00122 00123 // find the index of the given node in the factor cut 00124 NodeIndex = -1; 00125 for ( NodeIndex = 0; NodeIndex < (int)pCutF->nLeaves; NodeIndex++ ) 00126 if ( pCutF->pLeaves[NodeIndex] == Node ) 00127 break; 00128 assert( NodeIndex >= 0 ); // Node should be in pCutF 00129 00130 // copy the truth table 00131 Extra_TruthCopy( uTemp, Cut_CutReadTruth(pCutF), pCutF->nLeaves ); 00132 00133 // bubble-move the NodeIndex variable to be the last one (the most significant one) 00134 pIn = uTemp; pOut = uCof0; // uCof0 is used for temporary storage here 00135 for ( i = NodeIndex; i < (int)pCutF->nLeaves - 1; i++ ) 00136 { 00137 Extra_TruthSwapAdjacentVars( pOut, pIn, pCutF->nLeaves, i ); 00138 pTemp = pIn; pIn = pOut; pOut = pTemp; 00139 } 00140 if ( (pCutF->nLeaves - 1 - NodeIndex) & 1 ) 00141 Extra_TruthCopy( pOut, pIn, pCutF->nLeaves ); 00142 // the result of stretching is in uTemp 00143 00144 // cofactor the factor cut with respect to the node 00145 Extra_TruthCopy( uCof0, uTemp, pCutF->nLeaves ); 00146 Extra_TruthCofactor0( uCof0, pCutF->nLeaves, pCutF->nLeaves-1 ); 00147 Extra_TruthCopy( uCof1, uTemp, pCutF->nLeaves ); 00148 Extra_TruthCofactor1( uCof1, pCutF->nLeaves, pCutF->nLeaves-1 ); 00149 00150 // temporarily shrink the factor cut's variables by removing Node 00151 for ( i = NodeIndex; i < (int)pCutF->nLeaves - 1; i++ ) 00152 pCutF->pLeaves[i] = pCutF->pLeaves[i+1]; 00153 pCutF->nLeaves--; 00154 00155 // spread out the cofactors' truth tables to the same var order as the resulting cut 00156 uPhase = Cut_TruthPhase(pCutRes, pCutF); 00157 assert( Extra_WordCountOnes(uPhase) == (int)pCutF->nLeaves ); 00158 Extra_TruthStretch( uTemp, uCof0, pCutF->nLeaves, pCutF->nVarsMax, uPhase ); 00159 Extra_TruthCopy( uCof0, uTemp, pCutF->nVarsMax ); 00160 Extra_TruthStretch( uTemp, uCof1, pCutF->nLeaves, pCutF->nVarsMax, uPhase ); 00161 Extra_TruthCopy( uCof1, uTemp, pCutF->nVarsMax ); 00162 00163 // spread out the tree cut's truth table to the same var order as the resulting cut 00164 uPhase = Cut_TruthPhase(pCutRes, pCutT); 00165 assert( Extra_WordCountOnes(uPhase) == (int)pCutT->nLeaves ); 00166 Extra_TruthStretch( uTemp, Cut_CutReadTruth(pCutT), pCutT->nLeaves, pCutT->nVarsMax, uPhase ); 00167 00168 // create the resulting truth table 00169 pTemp = Cut_CutReadTruth(pCutRes); 00170 for ( i = Extra_TruthWordNum(pCutRes->nLeaves)-1; i >= 0; i-- ) 00171 pTemp[i] = (uCof0[i] & ~uTemp[i]) | (uCof1[i] & uTemp[i]); 00172 00173 // undo the removal of the node from the cut 00174 for ( i = (int)pCutF->nLeaves - 1; i >= NodeIndex; --i ) 00175 pCutF->pLeaves[i+1] = pCutF->pLeaves[i]; 00176 pCutF->pLeaves[NodeIndex] = Node; 00177 pCutF->nLeaves++; 00178 }
FUNCTION DEFINITIONS ///Function*************************************************************
Synopsis [Computes the stretching phase of the cut w.r.t. the merged cut.]
Description []
SideEffects []
SeeAlso []
Definition at line 44 of file cutExpand.c.
00045 { 00046 unsigned uPhase = 0; 00047 int i, k; 00048 for ( i = k = 0; i < (int)pCut->nLeaves; i++ ) 00049 { 00050 if ( k == (int)pCut1->nLeaves ) 00051 break; 00052 if ( pCut->pLeaves[i] < pCut1->pLeaves[k] ) 00053 continue; 00054 assert( pCut->pLeaves[i] == pCut1->pLeaves[k] ); 00055 uPhase |= (1 << i); 00056 k++; 00057 } 00058 return uPhase; 00059 }
 1.6.1
1.6.1