src/map/mapper/mapperTime.c File Reference
#include "mapperInt.h"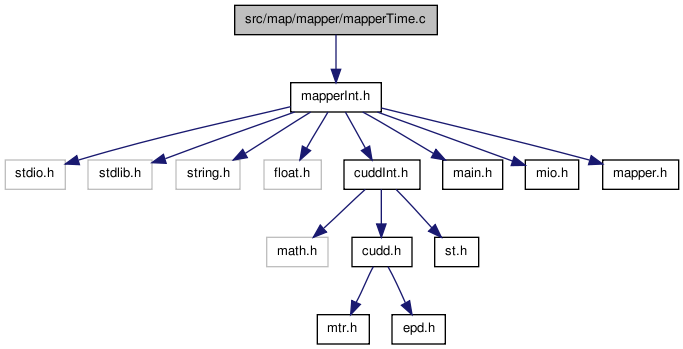
Go to the source code of this file.
Functions | |
| static void | Map_TimePropagateRequired (Map_Man_t *p, Map_NodeVec_t *vNodes) |
| static void | Map_TimePropagateRequiredPhase (Map_Man_t *p, Map_Node_t *pNode, int fPhase) |
| static float | Map_MatchComputeReqTimes (Map_Cut_t *pCut, int fPhase, Map_Time_t *ptArrRes) |
| float | Map_TimeMatchWithInverter (Map_Man_t *p, Map_Match_t *pMatch) |
| void | Map_TimeCutComputeArrival_rec (Map_Cut_t *pCut, int fPhase) |
| float | Map_TimeCutComputeArrival (Map_Node_t *pNode, Map_Cut_t *pCut, int fPhase, float tWorstLimit) |
| float | Map_TimeComputeArrivalMax (Map_Man_t *p) |
| void | Map_TimeComputeRequiredGlobal (Map_Man_t *p) |
| void | Map_TimeComputeRequired (Map_Man_t *p, float fRequired) |
Function Documentation
| float Map_MatchComputeReqTimes | ( | Map_Cut_t * | pCut, | |
| int | fPhase, | |||
| Map_Time_t * | ptArrRes | |||
| ) | [static] |
Function*************************************************************
Synopsis [Computes the arrival times of the cut.]
Description [Computes the arrival times of the cut if it is implemented using the given supergate with the given phase. Uses the constraint-type specification of rise/fall arrival times.]
SideEffects []
SeeAlso []
Definition at line 448 of file mapperTime.c.
00449 { 00450 Map_Time_t * ptArrIn; 00451 Map_Super_t * pSuper; 00452 unsigned uPhaseTot; 00453 int fPinPhase, i; 00454 float tDelay; 00455 00456 // get the supergate and the phase 00457 pSuper = pCut->M[fPhase].pSuperBest; 00458 uPhaseTot = pCut->M[fPhase].uPhaseBest; 00459 00460 // propagate the arrival times 00461 ptArrRes->Rise = ptArrRes->Fall = -MAP_FLOAT_LARGE; 00462 for ( i = 0; i < pCut->nLeaves; i++ ) 00463 { 00464 // get the phase of the given pin 00465 fPinPhase = ((uPhaseTot & (1 << i)) == 0); 00466 ptArrIn = pCut->ppLeaves[i]->tRequired + fPinPhase; 00467 // assert( ptArrIn->Worst < MAP_FLOAT_LARGE ); 00468 00469 // get the rise of the output due to rise of the inputs 00470 if ( pSuper->tDelaysR[i].Rise > 0 ) 00471 { 00472 tDelay = ptArrIn->Rise + pSuper->tDelaysR[i].Rise; 00473 if ( ptArrRes->Rise < tDelay ) 00474 ptArrRes->Rise = tDelay; 00475 } 00476 00477 // get the rise of the output due to fall of the inputs 00478 if ( pSuper->tDelaysR[i].Fall > 0 ) 00479 { 00480 tDelay = ptArrIn->Fall + pSuper->tDelaysR[i].Fall; 00481 if ( ptArrRes->Rise < tDelay ) 00482 ptArrRes->Rise = tDelay; 00483 } 00484 00485 // get the fall of the output due to rise of the inputs 00486 if ( pSuper->tDelaysF[i].Rise > 0 ) 00487 { 00488 tDelay = ptArrIn->Rise + pSuper->tDelaysF[i].Rise; 00489 if ( ptArrRes->Fall < tDelay ) 00490 ptArrRes->Fall = tDelay; 00491 } 00492 00493 // get the fall of the output due to fall of the inputs 00494 if ( pSuper->tDelaysF[i].Fall > 0 ) 00495 { 00496 tDelay = ptArrIn->Fall + pSuper->tDelaysF[i].Fall; 00497 if ( ptArrRes->Fall < tDelay ) 00498 ptArrRes->Fall = tDelay; 00499 } 00500 } 00501 // return the worst-case of rise/fall arrival times 00502 return MAP_MAX(ptArrRes->Rise, ptArrRes->Fall); 00503 }
| float Map_TimeComputeArrivalMax | ( | Map_Man_t * | p | ) |
Function*************************************************************
Synopsis [Computes the maximum arrival times.]
Description []
SideEffects []
SeeAlso []
Definition at line 168 of file mapperTime.c.
00169 { 00170 float tReqMax, tReq; 00171 int i, fPhase; 00172 // get the critical PO arrival time 00173 tReqMax = -MAP_FLOAT_LARGE; 00174 for ( i = 0; i < p->nOutputs; i++ ) 00175 { 00176 if ( Map_NodeIsConst(p->pOutputs[i]) ) 00177 continue; 00178 fPhase = !Map_IsComplement(p->pOutputs[i]); 00179 tReq = Map_Regular(p->pOutputs[i])->tArrival[fPhase].Worst; 00180 tReqMax = MAP_MAX( tReqMax, tReq ); 00181 } 00182 return tReqMax; 00183 }
| void Map_TimeComputeRequired | ( | Map_Man_t * | p, | |
| float | fRequired | |||
| ) |
Function*************************************************************
Synopsis [Computes the required times of all nodes.]
Description [This procedure assumes that the nodes used in the mapping are collected in p->vMapping.]
SideEffects []
SeeAlso []
Definition at line 229 of file mapperTime.c.
00230 { 00231 Map_Time_t * ptTime; 00232 int fPhase, i; 00233 00234 // clean the required times 00235 for ( i = 0; i < p->vAnds->nSize; i++ ) 00236 { 00237 p->vAnds->pArray[i]->tRequired[0].Rise = MAP_FLOAT_LARGE; 00238 p->vAnds->pArray[i]->tRequired[0].Fall = MAP_FLOAT_LARGE; 00239 p->vAnds->pArray[i]->tRequired[0].Worst = MAP_FLOAT_LARGE; 00240 p->vAnds->pArray[i]->tRequired[1].Rise = MAP_FLOAT_LARGE; 00241 p->vAnds->pArray[i]->tRequired[1].Fall = MAP_FLOAT_LARGE; 00242 p->vAnds->pArray[i]->tRequired[1].Worst = MAP_FLOAT_LARGE; 00243 } 00244 00245 // set the required times for the POs 00246 for ( i = 0; i < p->nOutputs; i++ ) 00247 { 00248 fPhase = !Map_IsComplement(p->pOutputs[i]); 00249 ptTime = Map_Regular(p->pOutputs[i])->tRequired + fPhase; 00250 ptTime->Rise = ptTime->Fall = ptTime->Worst = fRequired; 00251 } 00252 00253 // sorts the nodes in the decreasing order of levels 00254 // this puts the nodes in reverse topological order 00255 // Map_MappingSortByLevel( p, p->vMapping ); 00256 // the array is already sorted by construction in Map_MappingSetRefs() 00257 00258 Map_TimePropagateRequired( p, p->vMapping ); 00259 }
| void Map_TimeComputeRequiredGlobal | ( | Map_Man_t * | p | ) |
Function*************************************************************
Synopsis [Computes the required times of all nodes.]
Description []
SideEffects []
SeeAlso []
Definition at line 196 of file mapperTime.c.
00197 { 00198 p->fRequiredGlo = Map_TimeComputeArrivalMax( p ); 00199 // update the required times according to the target 00200 if ( p->DelayTarget != -1 ) 00201 { 00202 if ( p->fRequiredGlo > p->DelayTarget + p->fEpsilon ) 00203 { 00204 if ( p->fMappingMode == 1 ) 00205 printf( "Cannot meet the target required times (%4.2f). Continue anyway.\n", p->DelayTarget ); 00206 } 00207 else if ( p->fRequiredGlo < p->DelayTarget - p->fEpsilon ) 00208 { 00209 if ( p->fMappingMode == 1 ) 00210 printf( "Relaxing the required times from (%4.2f) to the target (%4.2f).\n", p->fRequiredGlo, p->DelayTarget ); 00211 p->fRequiredGlo = p->DelayTarget; 00212 } 00213 } 00214 Map_TimeComputeRequired( p, p->fRequiredGlo ); 00215 }
| float Map_TimeCutComputeArrival | ( | Map_Node_t * | pNode, | |
| Map_Cut_t * | pCut, | |||
| int | fPhase, | |||
| float | tWorstLimit | |||
| ) |
Function*************************************************************
Synopsis [Computes the arrival times of the cut.]
Description [Computes the arrival times of the cut if it is implemented using the given supergate with the given phase. Uses the constraint-type specification of rise/fall arrival times.]
SideEffects []
SeeAlso []
Definition at line 92 of file mapperTime.c.
00093 { 00094 Map_Match_t * pM = pCut->M + fPhase; 00095 Map_Super_t * pSuper = pM->pSuperBest; 00096 unsigned uPhaseTot = pM->uPhaseBest; 00097 Map_Time_t * ptArrRes = &pM->tArrive; 00098 Map_Time_t * ptArrIn; 00099 bool fPinPhase; 00100 float tDelay; 00101 int i; 00102 00103 ptArrRes->Rise = ptArrRes->Fall = 0.0; 00104 ptArrRes->Worst = MAP_FLOAT_LARGE; 00105 for ( i = pCut->nLeaves - 1; i >= 0; i-- ) 00106 { 00107 // get the phase of the given pin 00108 fPinPhase = ((uPhaseTot & (1 << i)) == 0); 00109 ptArrIn = pCut->ppLeaves[i]->tArrival + fPinPhase; 00110 00111 // get the rise of the output due to rise of the inputs 00112 if ( pSuper->tDelaysR[i].Rise > 0 ) 00113 { 00114 tDelay = ptArrIn->Rise + pSuper->tDelaysR[i].Rise; 00115 if ( tDelay > tWorstLimit ) 00116 return MAP_FLOAT_LARGE; 00117 if ( ptArrRes->Rise < tDelay ) 00118 ptArrRes->Rise = tDelay; 00119 } 00120 00121 // get the rise of the output due to fall of the inputs 00122 if ( pSuper->tDelaysR[i].Fall > 0 ) 00123 { 00124 tDelay = ptArrIn->Fall + pSuper->tDelaysR[i].Fall; 00125 if ( tDelay > tWorstLimit ) 00126 return MAP_FLOAT_LARGE; 00127 if ( ptArrRes->Rise < tDelay ) 00128 ptArrRes->Rise = tDelay; 00129 } 00130 00131 // get the fall of the output due to rise of the inputs 00132 if ( pSuper->tDelaysF[i].Rise > 0 ) 00133 { 00134 tDelay = ptArrIn->Rise + pSuper->tDelaysF[i].Rise; 00135 if ( tDelay > tWorstLimit ) 00136 return MAP_FLOAT_LARGE; 00137 if ( ptArrRes->Fall < tDelay ) 00138 ptArrRes->Fall = tDelay; 00139 } 00140 00141 // get the fall of the output due to fall of the inputs 00142 if ( pSuper->tDelaysF[i].Fall > 0 ) 00143 { 00144 tDelay = ptArrIn->Fall + pSuper->tDelaysF[i].Fall; 00145 if ( tDelay > tWorstLimit ) 00146 return MAP_FLOAT_LARGE; 00147 if ( ptArrRes->Fall < tDelay ) 00148 ptArrRes->Fall = tDelay; 00149 } 00150 } 00151 // return the worst-case of rise/fall arrival times 00152 ptArrRes->Worst = MAP_MAX(ptArrRes->Rise, ptArrRes->Fall); 00153 return ptArrRes->Worst; 00154 }
| void Map_TimeCutComputeArrival_rec | ( | Map_Cut_t * | pCut, | |
| int | fPhase | |||
| ) |
Function*************************************************************
Synopsis [Computes the arrival times of the cut recursively.]
Description [When computing the arrival time for the previously unused cuts, their arrival time may be incorrect because their fanins have incorrect arrival time. This procedure is called to fix this problem.]
SideEffects []
SeeAlso []
Definition at line 66 of file mapperTime.c.
00067 { 00068 int i, fPhaseLeaf; 00069 for ( i = 0; i < pCut->nLeaves; i++ ) 00070 { 00071 fPhaseLeaf = Map_CutGetLeafPhase( pCut, fPhase, i ); 00072 if ( pCut->ppLeaves[i]->nRefAct[fPhaseLeaf] > 0 ) 00073 continue; 00074 Map_TimeCutComputeArrival_rec( pCut->ppLeaves[i]->pCutBest[fPhaseLeaf], fPhaseLeaf ); 00075 } 00076 Map_TimeCutComputeArrival( NULL, pCut, fPhase, MAP_FLOAT_LARGE ); 00077 }
| float Map_TimeMatchWithInverter | ( | Map_Man_t * | p, | |
| Map_Match_t * | pMatch | |||
| ) |
FUNCTION DEFINITIONS ///function*************************************************************
synopsis [Computes the exact area associated with the cut.]
description []
sideeffects []
seealso []
Definition at line 44 of file mapperTime.c.
| void Map_TimePropagateRequired | ( | Map_Man_t * | p, | |
| Map_NodeVec_t * | vNodes | |||
| ) | [static] |
CFile****************************************************************
FileName [mapperTime.c]
PackageName [MVSIS 1.3: Multi-valued logic synthesis system.]
Synopsis [Generic technology mapping engine.]
Author [MVSIS Group]
Affiliation [UC Berkeley]
Date [Ver. 2.0. Started - June 1, 2004.]
Revision [
- Id
- mapperTime.c,v 1.3 2005/03/02 02:35:54 alanmi Exp
] DECLARATIONS ///
Function*************************************************************
Synopsis [Computes the required times of the given nodes.]
Description []
SideEffects []
SeeAlso []
Definition at line 272 of file mapperTime.c.
00273 { 00274 Map_Node_t * pNode; 00275 Map_Time_t tReqOutTest, * ptReqOutTest = &tReqOutTest; 00276 Map_Time_t * ptReqIn, * ptReqOut; 00277 int fPhase, k; 00278 00279 // go through the nodes in the reverse topological order 00280 for ( k = 0; k < vNodes->nSize; k++ ) 00281 { 00282 pNode = vNodes->pArray[k]; 00283 00284 // this computation works for regular nodes only 00285 assert( !Map_IsComplement(pNode) ); 00286 // at least one phase should be mapped 00287 assert( pNode->pCutBest[0] != NULL || pNode->pCutBest[1] != NULL ); 00288 // the node should be used in the currently assigned mapping 00289 assert( pNode->nRefAct[0] > 0 || pNode->nRefAct[1] > 0 ); 00290 00291 // if one of the cuts is not given, project the required times from the other cut 00292 if ( pNode->pCutBest[0] == NULL || pNode->pCutBest[1] == NULL ) 00293 { 00294 // assert( 0 ); 00295 // get the missing phase 00296 fPhase = (pNode->pCutBest[1] == NULL); 00297 // check if the missing phase is needed in the mapping 00298 if ( pNode->nRefAct[fPhase] > 0 ) 00299 { 00300 // get the pointers to the required times of the missing phase 00301 ptReqOut = pNode->tRequired + fPhase; 00302 // assert( ptReqOut->Fall < MAP_FLOAT_LARGE ); 00303 // get the pointers to the required times of the present phase 00304 ptReqIn = pNode->tRequired + !fPhase; 00305 // propagate the required times from the missing phase to the present phase 00306 // tArrInv.Fall = pMatch->tArrive.Rise + p->pSuperLib->tDelayInv.Fall; 00307 // tArrInv.Rise = pMatch->tArrive.Fall + p->pSuperLib->tDelayInv.Rise; 00308 ptReqIn->Fall = MAP_MIN( ptReqIn->Fall, ptReqOut->Rise - p->pSuperLib->tDelayInv.Rise ); 00309 ptReqIn->Rise = MAP_MIN( ptReqIn->Rise, ptReqOut->Fall - p->pSuperLib->tDelayInv.Fall ); 00310 } 00311 } 00312 00313 // finalize the worst case computation 00314 pNode->tRequired[0].Worst = MAP_MIN( pNode->tRequired[0].Fall, pNode->tRequired[0].Rise ); 00315 pNode->tRequired[1].Worst = MAP_MIN( pNode->tRequired[1].Fall, pNode->tRequired[1].Rise ); 00316 00317 // skip the PIs 00318 if ( !Map_NodeIsAnd(pNode) ) 00319 continue; 00320 00321 // propagate required times of different phases of the node 00322 // the ordering of phases does not matter since they are mapped independently 00323 if ( pNode->pCutBest[0] && pNode->tRequired[0].Worst < MAP_FLOAT_LARGE ) 00324 Map_TimePropagateRequiredPhase( p, pNode, 0 ); 00325 if ( pNode->pCutBest[1] && pNode->tRequired[1].Worst < MAP_FLOAT_LARGE ) 00326 Map_TimePropagateRequiredPhase( p, pNode, 1 ); 00327 } 00328 00329 // in the end, we verify the required times 00330 // for this, we compute the arrival times of the outputs of each phase 00331 // of the supergates using the fanins' required times as the fanins' arrival times 00332 // the resulting arrival time of the supergate should be less than the actual required time 00333 for ( k = 0; k < vNodes->nSize; k++ ) 00334 { 00335 pNode = vNodes->pArray[k]; 00336 if ( !Map_NodeIsAnd(pNode) ) 00337 continue; 00338 // verify that the required times are propagated correctly 00339 // if ( pNode->pCutBest[0] && (pNode->nRefAct[0] > 0 || pNode->pCutBest[1] == NULL) ) 00340 if ( pNode->pCutBest[0] && pNode->tRequired[0].Worst < MAP_FLOAT_LARGE ) 00341 { 00342 Map_MatchComputeReqTimes( pNode->pCutBest[0], 0, ptReqOutTest ); 00343 assert( ptReqOutTest->Rise < pNode->tRequired[0].Rise + p->fEpsilon ); 00344 assert( ptReqOutTest->Fall < pNode->tRequired[0].Fall + p->fEpsilon ); 00345 } 00346 // if ( pNode->pCutBest[1] && (pNode->nRefAct[1] > 0 || pNode->pCutBest[0] == NULL) ) 00347 if ( pNode->pCutBest[1] && pNode->tRequired[1].Worst < MAP_FLOAT_LARGE ) 00348 { 00349 Map_MatchComputeReqTimes( pNode->pCutBest[1], 1, ptReqOutTest ); 00350 assert( ptReqOutTest->Rise < pNode->tRequired[1].Rise + p->fEpsilon ); 00351 assert( ptReqOutTest->Fall < pNode->tRequired[1].Fall + p->fEpsilon ); 00352 } 00353 } 00354 00355 }
| void Map_TimePropagateRequiredPhase | ( | Map_Man_t * | p, | |
| Map_Node_t * | pNode, | |||
| int | fPhase | |||
| ) | [static] |
Function*************************************************************
Synopsis [Computes the required times of the given nodes.]
Description []
SideEffects []
SeeAlso []
Definition at line 368 of file mapperTime.c.
00369 { 00370 Map_Time_t * ptReqIn, * ptReqOut; 00371 Map_Cut_t * pCut; 00372 Map_Super_t * pSuper; 00373 float tNewReqTime; 00374 unsigned uPhase; 00375 int fPinPhase, i; 00376 00377 // get the cut to be propagated 00378 pCut = pNode->pCutBest[fPhase]; 00379 assert( pCut != NULL ); 00380 // get the supergate and its polarity 00381 pSuper = pCut->M[fPhase].pSuperBest; 00382 uPhase = pCut->M[fPhase].uPhaseBest; 00383 // get the required time of the output of the supergate 00384 ptReqOut = pNode->tRequired + fPhase; 00385 // set the required time of the children 00386 for ( i = 0; i < pCut->nLeaves; i++ ) 00387 { 00388 // get the phase of the given pin of the supergate 00389 fPinPhase = ((uPhase & (1 << i)) == 0); 00390 ptReqIn = pCut->ppLeaves[i]->tRequired + fPinPhase; 00391 assert( pCut->ppLeaves[i]->nRefAct[2] > 0 ); 00392 00393 // get the rise of the output due to rise of the inputs 00394 // if ( ptArrOut->Rise < ptArrIn->Rise + pSuper->tDelaysR[i].Rise ) 00395 // ptArrOut->Rise = ptArrIn->Rise + pSuper->tDelaysR[i].Rise; 00396 if ( pSuper->tDelaysR[i].Rise > 0 ) 00397 { 00398 tNewReqTime = ptReqOut->Rise - pSuper->tDelaysR[i].Rise; 00399 ptReqIn->Rise = MAP_MIN( ptReqIn->Rise, tNewReqTime ); 00400 } 00401 00402 // get the rise of the output due to fall of the inputs 00403 // if ( ptArrOut->Rise < ptArrIn->Fall + pSuper->tDelaysR[i].Fall ) 00404 // ptArrOut->Rise = ptArrIn->Fall + pSuper->tDelaysR[i].Fall; 00405 if ( pSuper->tDelaysR[i].Fall > 0 ) 00406 { 00407 tNewReqTime = ptReqOut->Rise - pSuper->tDelaysR[i].Fall; 00408 ptReqIn->Fall = MAP_MIN( ptReqIn->Fall, tNewReqTime ); 00409 } 00410 00411 // get the fall of the output due to rise of the inputs 00412 // if ( ptArrOut->Fall < ptArrIn->Rise + pSuper->tDelaysF[i].Rise ) 00413 // ptArrOut->Fall = ptArrIn->Rise + pSuper->tDelaysF[i].Rise; 00414 if ( pSuper->tDelaysF[i].Rise > 0 ) 00415 { 00416 tNewReqTime = ptReqOut->Fall - pSuper->tDelaysF[i].Rise; 00417 ptReqIn->Rise = MAP_MIN( ptReqIn->Rise, tNewReqTime ); 00418 } 00419 00420 // get the fall of the output due to fall of the inputs 00421 // if ( ptArrOut->Fall < ptArrIn->Fall + pSuper->tDelaysF[i].Fall ) 00422 // ptArrOut->Fall = ptArrIn->Fall + pSuper->tDelaysF[i].Fall; 00423 if ( pSuper->tDelaysF[i].Fall > 0 ) 00424 { 00425 tNewReqTime = ptReqOut->Fall - pSuper->tDelaysF[i].Fall; 00426 ptReqIn->Fall = MAP_MIN( ptReqIn->Fall, tNewReqTime ); 00427 } 00428 } 00429 00430 // compare the required times with the arrival times 00431 assert( pNode->tArrival[fPhase].Rise < ptReqOut->Rise + p->fEpsilon ); 00432 assert( pNode->tArrival[fPhase].Fall < ptReqOut->Fall + p->fEpsilon ); 00433 }
 1.6.1
1.6.1