src/opt/cut/cutMerge.c File Reference
#include "cutInt.h"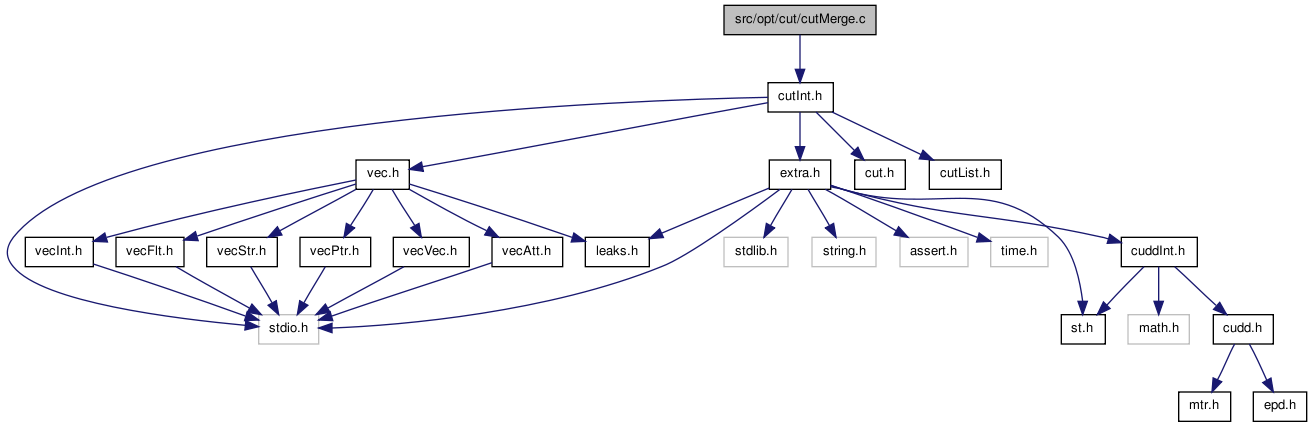
Go to the source code of this file.
Functions | |
| Cut_Cut_t * | Cut_CutMergeTwo2 (Cut_Man_t *p, Cut_Cut_t *pCut0, Cut_Cut_t *pCut1) |
| Cut_Cut_t * | Cut_CutMergeTwo (Cut_Man_t *p, Cut_Cut_t *pCut0, Cut_Cut_t *pCut1) |
| Cut_Cut_t * | Cut_CutMergeTwo3 (Cut_Man_t *p, Cut_Cut_t *pCut0, Cut_Cut_t *pCut1) |
| Cut_Cut_t * | Cut_CutMergeTwo4 (Cut_Man_t *p, Cut_Cut_t *pCut0, Cut_Cut_t *pCut1) |
| Cut_Cut_t * | Cut_CutMergeTwo5 (Cut_Man_t *p, Cut_Cut_t *pCut0, Cut_Cut_t *pCut1) |
Function Documentation
Function*************************************************************
Synopsis [Merges two cuts.]
Description []
SideEffects []
SeeAlso []
Definition at line 167 of file cutMerge.c.
00168 { 00169 Cut_Cut_t * pRes; 00170 int * pLeaves; 00171 int Limit, nLeaves0, nLeaves1; 00172 int i, k, c; 00173 00174 assert( pCut0->nLeaves >= pCut1->nLeaves ); 00175 00176 // consider two cuts 00177 nLeaves0 = pCut0->nLeaves; 00178 nLeaves1 = pCut1->nLeaves; 00179 00180 // the case of the largest cut sizes 00181 Limit = p->pParams->nVarsMax; 00182 if ( nLeaves0 == Limit && nLeaves1 == Limit ) 00183 { 00184 for ( i = 0; i < nLeaves0; i++ ) 00185 if ( pCut0->pLeaves[i] != pCut1->pLeaves[i] ) 00186 return NULL; 00187 pRes = Cut_CutAlloc( p ); 00188 for ( i = 0; i < nLeaves0; i++ ) 00189 pRes->pLeaves[i] = pCut0->pLeaves[i]; 00190 pRes->nLeaves = pCut0->nLeaves; 00191 return pRes; 00192 } 00193 // the case when one of the cuts is the largest 00194 if ( nLeaves0 == Limit ) 00195 { 00196 for ( i = 0; i < nLeaves1; i++ ) 00197 { 00198 for ( k = nLeaves0 - 1; k >= 0; k-- ) 00199 if ( pCut0->pLeaves[k] == pCut1->pLeaves[i] ) 00200 break; 00201 if ( k == -1 ) // did not find 00202 return NULL; 00203 } 00204 pRes = Cut_CutAlloc( p ); 00205 for ( i = 0; i < nLeaves0; i++ ) 00206 pRes->pLeaves[i] = pCut0->pLeaves[i]; 00207 pRes->nLeaves = pCut0->nLeaves; 00208 return pRes; 00209 } 00210 00211 // prepare the cut 00212 if ( p->pReady == NULL ) 00213 p->pReady = Cut_CutAlloc( p ); 00214 pLeaves = p->pReady->pLeaves; 00215 00216 // compare two cuts with different numbers 00217 i = k = 0; 00218 for ( c = 0; c < Limit; c++ ) 00219 { 00220 if ( k == nLeaves1 ) 00221 { 00222 if ( i == nLeaves0 ) 00223 { 00224 p->pReady->nLeaves = c; 00225 pRes = p->pReady; p->pReady = NULL; 00226 return pRes; 00227 } 00228 pLeaves[c] = pCut0->pLeaves[i++]; 00229 continue; 00230 } 00231 if ( i == nLeaves0 ) 00232 { 00233 if ( k == nLeaves1 ) 00234 { 00235 p->pReady->nLeaves = c; 00236 pRes = p->pReady; p->pReady = NULL; 00237 return pRes; 00238 } 00239 pLeaves[c] = pCut1->pLeaves[k++]; 00240 continue; 00241 } 00242 if ( pCut0->pLeaves[i] < pCut1->pLeaves[k] ) 00243 { 00244 pLeaves[c] = pCut0->pLeaves[i++]; 00245 continue; 00246 } 00247 if ( pCut0->pLeaves[i] > pCut1->pLeaves[k] ) 00248 { 00249 pLeaves[c] = pCut1->pLeaves[k++]; 00250 continue; 00251 } 00252 pLeaves[c] = pCut0->pLeaves[i++]; 00253 k++; 00254 } 00255 if ( i < nLeaves0 || k < nLeaves1 ) 00256 return NULL; 00257 p->pReady->nLeaves = c; 00258 pRes = p->pReady; p->pReady = NULL; 00259 return pRes; 00260 }
CFile****************************************************************
FileName [cutMerge.c]
SystemName [ABC: Logic synthesis and verification system.]
PackageName [K-feasible cut computation package.]
Synopsis [Procedure to merge two cuts.]
Author [Alan Mishchenko]
Affiliation [UC Berkeley]
Date [Ver. 1.0. Started - June 20, 2005.]
Revision [
- Id
- cutMerge.c,v 1.00 2005/06/20 00:00:00 alanmi Exp
] DECLARATIONS /// FUNCTION DEFINITIONS ///Function*************************************************************
Synopsis [Merges two cuts.]
Description [This procedure works.]
SideEffects []
SeeAlso []
Definition at line 42 of file cutMerge.c.
00043 { 00044 static int M[7][3] = {{0},{0},{0},{0},{0},{0},{0}}; 00045 Cut_Cut_t * pRes; 00046 int * pRow; 00047 int nLeaves0, nLeaves1, Limit; 00048 int i, k, Count, nNodes; 00049 00050 assert( pCut0->nLeaves >= pCut1->nLeaves ); 00051 00052 // the case of the largest cut sizes 00053 Limit = p->pParams->nVarsMax; 00054 nLeaves0 = pCut0->nLeaves; 00055 nLeaves1 = pCut1->nLeaves; 00056 if ( nLeaves0 == Limit && nLeaves1 == Limit ) 00057 { 00058 for ( i = 0; i < nLeaves0; i++ ) 00059 if ( pCut0->pLeaves[i] != pCut1->pLeaves[i] ) 00060 return NULL; 00061 pRes = Cut_CutAlloc( p ); 00062 for ( i = 0; i < nLeaves0; i++ ) 00063 pRes->pLeaves[i] = pCut0->pLeaves[i]; 00064 pRes->nLeaves = nLeaves0; 00065 return pRes; 00066 } 00067 // the case when one of the cuts is the largest 00068 if ( nLeaves0 == Limit ) 00069 { 00070 for ( i = 0; i < nLeaves1; i++ ) 00071 { 00072 for ( k = nLeaves0 - 1; k >= 0; k-- ) 00073 if ( pCut0->pLeaves[k] == pCut1->pLeaves[i] ) 00074 break; 00075 if ( k == -1 ) // did not find 00076 return NULL; 00077 } 00078 pRes = Cut_CutAlloc( p ); 00079 for ( i = 0; i < nLeaves0; i++ ) 00080 pRes->pLeaves[i] = pCut0->pLeaves[i]; 00081 pRes->nLeaves = nLeaves0; 00082 return pRes; 00083 } 00084 // other cases 00085 nNodes = nLeaves0; 00086 for ( i = 0; i < nLeaves1; i++ ) 00087 { 00088 for ( k = nLeaves0 - 1; k >= 0; k-- ) 00089 { 00090 if ( pCut0->pLeaves[k] > pCut1->pLeaves[i] ) 00091 continue; 00092 if ( pCut0->pLeaves[k] < pCut1->pLeaves[i] ) 00093 { 00094 pRow = M[k+1]; 00095 if ( pRow[0] == 0 ) 00096 pRow[0] = pCut1->pLeaves[i], pRow[1] = 0; 00097 else if ( pRow[1] == 0 ) 00098 pRow[1] = pCut1->pLeaves[i], pRow[2] = 0; 00099 else if ( pRow[2] == 0 ) 00100 pRow[2] = pCut1->pLeaves[i]; 00101 else 00102 assert( 0 ); 00103 if ( ++nNodes > Limit ) 00104 { 00105 for ( i = 0; i <= nLeaves0; i++ ) 00106 M[i][0] = 0; 00107 return NULL; 00108 } 00109 } 00110 break; 00111 } 00112 if ( k == -1 ) 00113 { 00114 pRow = M[0]; 00115 if ( pRow[0] == 0 ) 00116 pRow[0] = pCut1->pLeaves[i], pRow[1] = 0; 00117 else if ( pRow[1] == 0 ) 00118 pRow[1] = pCut1->pLeaves[i], pRow[2] = 0; 00119 else if ( pRow[2] == 0 ) 00120 pRow[2] = pCut1->pLeaves[i]; 00121 else 00122 assert( 0 ); 00123 if ( ++nNodes > Limit ) 00124 { 00125 for ( i = 0; i <= nLeaves0; i++ ) 00126 M[i][0] = 0; 00127 return NULL; 00128 } 00129 continue; 00130 } 00131 } 00132 00133 pRes = Cut_CutAlloc( p ); 00134 for ( Count = 0, i = 0; i <= nLeaves0; i++ ) 00135 { 00136 if ( i > 0 ) 00137 pRes->pLeaves[Count++] = pCut0->pLeaves[i-1]; 00138 pRow = M[i]; 00139 if ( pRow[0] ) 00140 { 00141 pRes->pLeaves[Count++] = pRow[0]; 00142 if ( pRow[1] ) 00143 { 00144 pRes->pLeaves[Count++] = pRow[1]; 00145 if ( pRow[2] ) 00146 pRes->pLeaves[Count++] = pRow[2]; 00147 } 00148 pRow[0] = 0; 00149 } 00150 } 00151 assert( Count == nNodes ); 00152 pRes->nLeaves = nNodes; 00153 return pRes; 00154 }
Function*************************************************************
Synopsis [Merges two cuts.]
Description []
SideEffects []
SeeAlso []
Definition at line 274 of file cutMerge.c.
00275 { 00276 Cut_Cut_t * pRes; 00277 int * pLeaves; 00278 int Limit, nLeaves0, nLeaves1; 00279 int i, k, c; 00280 00281 assert( pCut0->nLeaves >= pCut1->nLeaves ); 00282 00283 // prepare the cut 00284 if ( p->pReady == NULL ) 00285 p->pReady = Cut_CutAlloc( p ); 00286 pLeaves = p->pReady->pLeaves; 00287 00288 // consider two cuts 00289 Limit = p->pParams->nVarsMax; 00290 nLeaves0 = pCut0->nLeaves; 00291 nLeaves1 = pCut1->nLeaves; 00292 if ( nLeaves0 == Limit ) 00293 { // the case when one of the cuts is the largest 00294 if ( nLeaves1 == Limit ) 00295 { // the case when both cuts are the largest 00296 for ( i = 0; i < nLeaves0; i++ ) 00297 { 00298 pLeaves[i] = pCut0->pLeaves[i]; 00299 if ( pLeaves[i] != pCut1->pLeaves[i] ) 00300 return NULL; 00301 } 00302 } 00303 else 00304 { 00305 for ( i = k = 0; i < nLeaves0; i++ ) 00306 { 00307 pLeaves[i] = pCut0->pLeaves[i]; 00308 if ( k == (int)nLeaves1 ) 00309 continue; 00310 if ( pLeaves[i] < pCut1->pLeaves[k] ) 00311 continue; 00312 if ( pLeaves[i] == pCut1->pLeaves[k++] ) 00313 continue; 00314 return NULL; 00315 } 00316 if ( k < nLeaves1 ) 00317 return NULL; 00318 } 00319 p->pReady->nLeaves = nLeaves0; 00320 pRes = p->pReady; p->pReady = NULL; 00321 return pRes; 00322 } 00323 00324 // compare two cuts with different numbers 00325 i = k = 0; 00326 for ( c = 0; c < Limit; c++ ) 00327 { 00328 if ( k == nLeaves1 ) 00329 { 00330 if ( i == nLeaves0 ) 00331 { 00332 p->pReady->nLeaves = c; 00333 pRes = p->pReady; p->pReady = NULL; 00334 return pRes; 00335 } 00336 pLeaves[c] = pCut0->pLeaves[i++]; 00337 continue; 00338 } 00339 if ( i == nLeaves0 ) 00340 { 00341 if ( k == nLeaves1 ) 00342 { 00343 p->pReady->nLeaves = c; 00344 pRes = p->pReady; p->pReady = NULL; 00345 return pRes; 00346 } 00347 pLeaves[c] = pCut1->pLeaves[k++]; 00348 continue; 00349 } 00350 if ( pCut0->pLeaves[i] < pCut1->pLeaves[k] ) 00351 { 00352 pLeaves[c] = pCut0->pLeaves[i++]; 00353 continue; 00354 } 00355 if ( pCut0->pLeaves[i] > pCut1->pLeaves[k] ) 00356 { 00357 pLeaves[c] = pCut1->pLeaves[k++]; 00358 continue; 00359 } 00360 pLeaves[c] = pCut0->pLeaves[i++]; 00361 k++; 00362 } 00363 if ( i < nLeaves0 || k < nLeaves1 ) 00364 return NULL; 00365 p->pReady->nLeaves = c; 00366 pRes = p->pReady; p->pReady = NULL; 00367 return pRes; 00368 }
Function*************************************************************
Synopsis [Merges two cuts.]
Description []
SideEffects []
SeeAlso []
Definition at line 381 of file cutMerge.c.
00382 { 00383 Cut_Cut_t * pRes; 00384 int * pLeaves; 00385 int i, k, min, NodeTemp, Limit, nTotal; 00386 00387 assert( pCut0->nLeaves >= pCut1->nLeaves ); 00388 00389 // prepare the cut 00390 if ( p->pReady == NULL ) 00391 p->pReady = Cut_CutAlloc( p ); 00392 pLeaves = p->pReady->pLeaves; 00393 00394 // consider two cuts 00395 Limit = p->pParams->nVarsMax; 00396 if ( pCut0->nLeaves == (unsigned)Limit ) 00397 { // the case when one of the cuts is the largest 00398 if ( pCut1->nLeaves == (unsigned)Limit ) 00399 { // the case when both cuts are the largest 00400 for ( i = 0; i < (int)pCut0->nLeaves; i++ ) 00401 { 00402 pLeaves[i] = pCut0->pLeaves[i]; 00403 if ( pLeaves[i] != pCut1->pLeaves[i] ) 00404 return NULL; 00405 } 00406 } 00407 else 00408 { 00409 for ( i = k = 0; i < (int)pCut0->nLeaves; i++ ) 00410 { 00411 pLeaves[i] = pCut0->pLeaves[i]; 00412 if ( k == (int)pCut1->nLeaves ) 00413 continue; 00414 if ( pLeaves[i] < pCut1->pLeaves[k] ) 00415 continue; 00416 if ( pLeaves[i] == pCut1->pLeaves[k++] ) 00417 continue; 00418 return NULL; 00419 } 00420 if ( k < (int)pCut1->nLeaves ) 00421 return NULL; 00422 } 00423 p->pReady->nLeaves = pCut0->nLeaves; 00424 pRes = p->pReady; p->pReady = NULL; 00425 return pRes; 00426 } 00427 00428 // count the number of unique entries in pCut1 00429 nTotal = pCut0->nLeaves; 00430 for ( i = 0; i < (int)pCut1->nLeaves; i++ ) 00431 { 00432 // try to find this entry among the leaves of pCut0 00433 for ( k = 0; k < (int)pCut0->nLeaves; k++ ) 00434 if ( pCut1->pLeaves[i] == pCut0->pLeaves[k] ) 00435 break; 00436 if ( k < (int)pCut0->nLeaves ) // found 00437 continue; 00438 // we found a new entry to add 00439 if ( nTotal == Limit ) 00440 return NULL; 00441 pLeaves[nTotal++] = pCut1->pLeaves[i]; 00442 } 00443 // we know that the feasible cut exists 00444 00445 // add the starting entries 00446 for ( k = 0; k < (int)pCut0->nLeaves; k++ ) 00447 pLeaves[k] = pCut0->pLeaves[k]; 00448 00449 // selection-sort the entries 00450 for ( i = 0; i < nTotal - 1; i++ ) 00451 { 00452 min = i; 00453 for ( k = i+1; k < nTotal; k++ ) 00454 if ( pLeaves[k] < pLeaves[min] ) 00455 min = k; 00456 NodeTemp = pLeaves[i]; 00457 pLeaves[i] = pLeaves[min]; 00458 pLeaves[min] = NodeTemp; 00459 } 00460 p->pReady->nLeaves = nTotal; 00461 pRes = p->pReady; p->pReady = NULL; 00462 return pRes; 00463 }
Function*************************************************************
Synopsis [Merges two cuts.]
Description [This procedure works.]
SideEffects []
SeeAlso []
Definition at line 476 of file cutMerge.c.
00477 { 00478 static int M[7][3] = {{0},{0},{0},{0},{0},{0},{0}}; 00479 Cut_Cut_t * pRes; 00480 int * pRow; 00481 unsigned uSign0, uSign1; 00482 int i, k, nNodes, Count; 00483 unsigned Limit = p->pParams->nVarsMax; 00484 00485 assert( pCut0->nLeaves >= pCut1->nLeaves ); 00486 00487 // the case of the largest cut sizes 00488 if ( pCut0->nLeaves == Limit && pCut1->nLeaves == Limit ) 00489 { 00490 for ( i = 0; i < (int)pCut0->nLeaves; i++ ) 00491 if ( pCut0->pLeaves[i] != pCut1->pLeaves[i] ) 00492 return NULL; 00493 pRes = Cut_CutAlloc( p ); 00494 for ( i = 0; i < (int)pCut0->nLeaves; i++ ) 00495 pRes->pLeaves[i] = pCut0->pLeaves[i]; 00496 pRes->nLeaves = pCut0->nLeaves; 00497 return pRes; 00498 } 00499 // the case when one of the cuts is the largest 00500 if ( pCut0->nLeaves == Limit ) 00501 { 00502 if ( !p->pParams->fTruth ) 00503 { 00504 for ( i = 0; i < (int)pCut1->nLeaves; i++ ) 00505 { 00506 for ( k = pCut0->nLeaves - 1; k >= 0; k-- ) 00507 if ( pCut0->pLeaves[k] == pCut1->pLeaves[i] ) 00508 break; 00509 if ( k == -1 ) // did not find 00510 return NULL; 00511 } 00512 pRes = Cut_CutAlloc( p ); 00513 } 00514 else 00515 { 00516 uSign1 = 0; 00517 for ( i = 0; i < (int)pCut1->nLeaves; i++ ) 00518 { 00519 for ( k = pCut0->nLeaves - 1; k >= 0; k-- ) 00520 if ( pCut0->pLeaves[k] == pCut1->pLeaves[i] ) 00521 { 00522 uSign1 |= (1 << i); 00523 break; 00524 } 00525 if ( k == -1 ) // did not find 00526 return NULL; 00527 } 00528 pRes = Cut_CutAlloc( p ); 00529 pRes->Num1 = uSign1; 00530 } 00531 for ( i = 0; i < (int)pCut0->nLeaves; i++ ) 00532 pRes->pLeaves[i] = pCut0->pLeaves[i]; 00533 pRes->nLeaves = pCut0->nLeaves; 00534 return pRes; 00535 } 00536 // other cases 00537 nNodes = pCut0->nLeaves; 00538 for ( i = 0; i < (int)pCut1->nLeaves; i++ ) 00539 { 00540 for ( k = pCut0->nLeaves - 1; k >= 0; k-- ) 00541 { 00542 if ( pCut0->pLeaves[k] > pCut1->pLeaves[i] ) 00543 continue; 00544 if ( pCut0->pLeaves[k] < pCut1->pLeaves[i] ) 00545 { 00546 pRow = M[k+1]; 00547 if ( pRow[0] == 0 ) 00548 pRow[0] = pCut1->pLeaves[i], pRow[1] = 0; 00549 else if ( pRow[1] == 0 ) 00550 pRow[1] = pCut1->pLeaves[i], pRow[2] = 0; 00551 else if ( pRow[2] == 0 ) 00552 pRow[2] = pCut1->pLeaves[i]; 00553 else 00554 assert( 0 ); 00555 if ( ++nNodes > (int)Limit ) 00556 { 00557 for ( i = 0; i <= (int)pCut0->nLeaves; i++ ) 00558 M[i][0] = 0; 00559 return NULL; 00560 } 00561 } 00562 break; 00563 } 00564 if ( k == -1 ) 00565 { 00566 pRow = M[0]; 00567 if ( pRow[0] == 0 ) 00568 pRow[0] = pCut1->pLeaves[i], pRow[1] = 0; 00569 else if ( pRow[1] == 0 ) 00570 pRow[1] = pCut1->pLeaves[i], pRow[2] = 0; 00571 else if ( pRow[2] == 0 ) 00572 pRow[2] = pCut1->pLeaves[i]; 00573 else 00574 assert( 0 ); 00575 if ( ++nNodes > (int)Limit ) 00576 { 00577 for ( i = 0; i <= (int)pCut0->nLeaves; i++ ) 00578 M[i][0] = 0; 00579 return NULL; 00580 } 00581 continue; 00582 } 00583 } 00584 00585 pRes = Cut_CutAlloc( p ); 00586 if ( !p->pParams->fTruth ) 00587 { 00588 for ( Count = 0, i = 0; i <= (int)pCut0->nLeaves; i++ ) 00589 { 00590 if ( i > 0 ) 00591 pRes->pLeaves[Count++] = pCut0->pLeaves[i-1]; 00592 pRow = M[i]; 00593 if ( pRow[0] ) 00594 { 00595 pRes->pLeaves[Count++] = pRow[0]; 00596 if ( pRow[1] ) 00597 { 00598 pRes->pLeaves[Count++] = pRow[1]; 00599 if ( pRow[2] ) 00600 pRes->pLeaves[Count++] = pRow[2]; 00601 } 00602 pRow[0] = 0; 00603 } 00604 } 00605 assert( Count == nNodes ); 00606 pRes->nLeaves = nNodes; 00607 /* 00608 // make sure that the cut is correct 00609 { 00610 for ( i = 1; i < (int)pRes->nLeaves; i++ ) 00611 if ( pRes->pLeaves[i-1] >= pRes->pLeaves[i] ) 00612 { 00613 int v = 0; 00614 } 00615 } 00616 */ 00617 return pRes; 00618 } 00619 00620 uSign0 = uSign1 = 0; 00621 for ( Count = 0, i = 0; i <= (int)pCut0->nLeaves; i++ ) 00622 { 00623 if ( i > 0 ) 00624 { 00625 uSign0 |= (1 << Count); 00626 pRes->pLeaves[Count++] = pCut1->pLeaves[i-1]; 00627 } 00628 pRow = M[i]; 00629 if ( pRow[0] ) 00630 { 00631 uSign1 |= (1 << Count); 00632 pRes->pLeaves[Count++] = pRow[0]; 00633 if ( pRow[1] ) 00634 { 00635 uSign1 |= (1 << Count); 00636 pRes->pLeaves[Count++] = pRow[1]; 00637 if ( pRow[2] ) 00638 { 00639 uSign1 |= (1 << Count); 00640 pRes->pLeaves[Count++] = pRow[2]; 00641 } 00642 } 00643 pRow[0] = 0; 00644 } 00645 } 00646 assert( Count == nNodes ); 00647 pRes->nLeaves = nNodes; 00648 pRes->Num1 = uSign1; 00649 pRes->Num0 = uSign0; 00650 return pRes; 00651 }
 1.6.1
1.6.1