src/base/abci/abcSat.c File Reference

#include "abc.h"
#include "satSolver.h"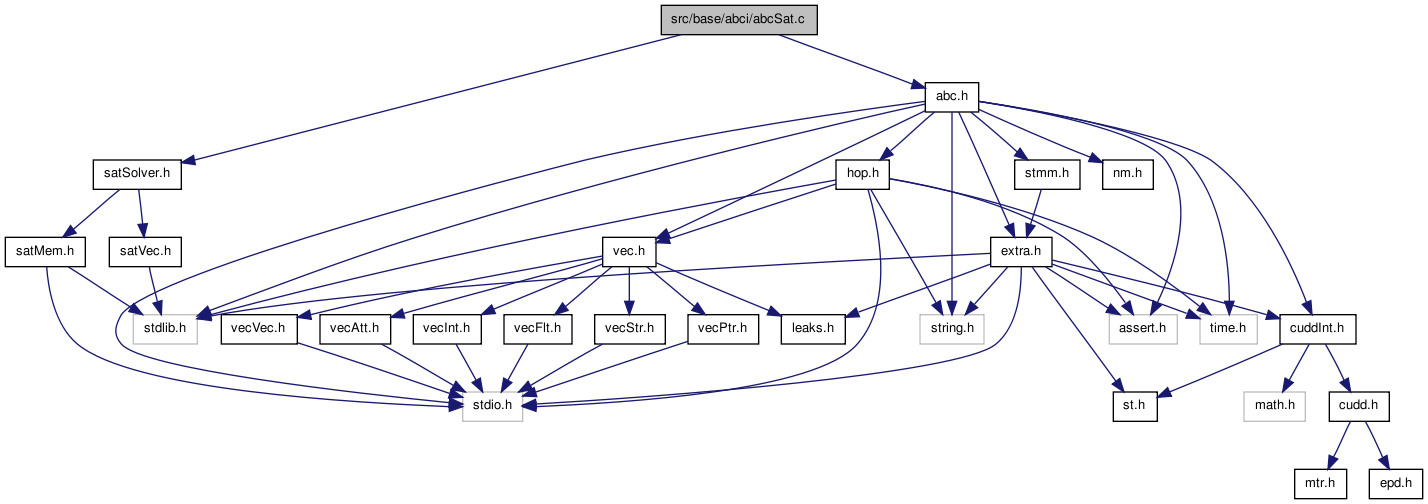
Include dependency graph for abcSat.c:

Go to the source code of this file.

Functions

static sat_solver * Abc_NtkMiterSatCreateLogic (Abc_Ntk_t *pNtk, int fAllPrimes)
Vec_Int_t * Abc_NtkGetCiSatVarNums (Abc_Ntk_t *pNtk)
int Abc_NtkMiterSat (Abc_Ntk_t *pNtk, sint64 nConfLimit, sint64 nInsLimit, int fVerbose, sint64 *pNumConfs, sint64 *pNumInspects)
int Abc_NtkClauseTriv (sat_solver *pSat, Abc_Obj_t *pNode, Vec_Int_t *vVars)
int Abc_NtkClauseTop (sat_solver *pSat, Vec_Ptr_t *vNodes, Vec_Int_t *vVars)
int Abc_NtkClauseAnd (sat_solver *pSat, Abc_Obj_t *pNode, Vec_Ptr_t *vSuper, Vec_Int_t *vVars)
int Abc_NtkClauseMux (sat_solver *pSat, Abc_Obj_t *pNode, Abc_Obj_t *pNodeC, Abc_Obj_t *pNodeT, Abc_Obj_t *pNodeE, Vec_Int_t *vVars)
int Abc_NtkCollectSupergate_rec (Abc_Obj_t *pNode, Vec_Ptr_t *vSuper, int fFirst, int fStopAtMux)
void Abc_NtkCollectSupergate (Abc_Obj_t *pNode, int fStopAtMux, Vec_Ptr_t *vNodes)
int Abc_NtkNodeFactor (Abc_Obj_t *pObj, int nLevelMax)
int Abc_NtkMiterSatCreateInt (sat_solver *pSat, Abc_Ntk_t *pNtk)
void * Abc_NtkMiterSatCreate (Abc_Ntk_t *pNtk, int fAllPrimes)
int Abc_NodeAddClauses (sat_solver *pSat, char *pSop0, char *pSop1, Abc_Obj_t *pNode, Vec_Int_t *vVars)
int Abc_NodeAddClausesTop (sat_solver *pSat, Abc_Obj_t *pNode, Vec_Int_t *vVars)

Variables

static nMuxes

Function Documentation

int Abc_NodeAddClauses ( sat_solver *  pSat,
char *  pSop0,
char *  pSop1,
Abc_Obj_t *  pNode,
Vec_Int_t *  vVars 
)

Function*************************************************************

Synopsis [Adds clauses for the internal node.]

Description []

SideEffects []

SeeAlso []

Definition at line 657 of file abcSat.c.

00658 {
00659     Abc_Obj_t * pFanin;
00660     int i, c, nFanins;
00661     int RetValue;
00662     char * pCube;
00663 
00664     nFanins = Abc_ObjFaninNum( pNode );
00665     assert( nFanins == Abc_SopGetVarNum( pSop0 ) );
00666 
00667 //    if ( nFanins == 0 )
00668     if ( Cudd_Regular(pNode->pData) == Cudd_ReadOne(pNode->pNtk->pManFunc) )
00669     {
00670         vVars->nSize = 0;
00671 //        if ( Abc_SopIsConst1(pSop1) )
00672         if ( !Cudd_IsComplement(pNode->pData) )
00673             Vec_IntPush( vVars, toLit(pNode->Id) );
00674         else
00675             Vec_IntPush( vVars, lit_neg(toLit(pNode->Id)) );
00676         RetValue = sat_solver_addclause( pSat, vVars->pArray, vVars->pArray + vVars->nSize );
00677         if ( !RetValue ) 
00678         {
00679             printf( "The CNF is trivially UNSAT.\n" );
00680             return 0;
00681         }
00682         return 1;
00683     }
00684  
00685     // add clauses for the negative phase
00686     for ( c = 0; ; c++ )
00687     {
00688         // get the cube
00689         pCube = pSop0 + c * (nFanins + 3);
00690         if ( *pCube == 0 )
00691             break;
00692         // add the clause
00693         vVars->nSize = 0;
00694         Abc_ObjForEachFanin( pNode, pFanin, i )
00695         {
00696             if ( pCube[i] == '0' )
00697                 Vec_IntPush( vVars, toLit(pFanin->Id) );
00698             else if ( pCube[i] == '1' )
00699                 Vec_IntPush( vVars, lit_neg(toLit(pFanin->Id)) );
00700         }
00701         Vec_IntPush( vVars, lit_neg(toLit(pNode->Id)) );
00702         RetValue = sat_solver_addclause( pSat, vVars->pArray, vVars->pArray + vVars->nSize );
00703         if ( !RetValue ) 
00704         {
00705             printf( "The CNF is trivially UNSAT.\n" );
00706             return 0;
00707         }
00708     }
00709 
00710     // add clauses for the positive phase
00711     for ( c = 0; ; c++ )
00712     {
00713         // get the cube
00714         pCube = pSop1 + c * (nFanins + 3);
00715         if ( *pCube == 0 )
00716             break;
00717         // add the clause
00718         vVars->nSize = 0;
00719         Abc_ObjForEachFanin( pNode, pFanin, i )
00720         {
00721             if ( pCube[i] == '0' )
00722                 Vec_IntPush( vVars, toLit(pFanin->Id) );
00723             else if ( pCube[i] == '1' )
00724                 Vec_IntPush( vVars, lit_neg(toLit(pFanin->Id)) );
00725         }
00726         Vec_IntPush( vVars, toLit(pNode->Id) );
00727         RetValue = sat_solver_addclause( pSat, vVars->pArray, vVars->pArray + vVars->nSize );
00728         if ( !RetValue ) 
00729         {
00730             printf( "The CNF is trivially UNSAT.\n" );
00731             return 0;
00732         }
00733     }
00734     return 1;
00735 }

int Abc_NodeAddClausesTop ( sat_solver *  pSat,
Abc_Obj_t *  pNode,
Vec_Int_t *  vVars 
)

Function*************************************************************

Synopsis [Adds clauses for the PO node.]

Description []

SideEffects []

SeeAlso []

Definition at line 748 of file abcSat.c.

00749 {
00750     Abc_Obj_t * pFanin;
00751     int RetValue;
00752 
00753     pFanin = Abc_ObjFanin0(pNode);
00754     if ( Abc_ObjFaninC0(pNode) )
00755     {
00756         vVars->nSize = 0;
00757         Vec_IntPush( vVars, toLit(pFanin->Id) );
00758         Vec_IntPush( vVars, toLit(pNode->Id) );
00759         RetValue = sat_solver_addclause( pSat, vVars->pArray, vVars->pArray + vVars->nSize );
00760         if ( !RetValue ) 
00761         {
00762             printf( "The CNF is trivially UNSAT.\n" );
00763             return 0;
00764         }
00765 
00766         vVars->nSize = 0;
00767         Vec_IntPush( vVars, lit_neg(toLit(pFanin->Id)) );
00768         Vec_IntPush( vVars, lit_neg(toLit(pNode->Id)) );
00769         RetValue = sat_solver_addclause( pSat, vVars->pArray, vVars->pArray + vVars->nSize );
00770         if ( !RetValue ) 
00771         {
00772             printf( "The CNF is trivially UNSAT.\n" );
00773             return 0;
00774         }
00775     }
00776     else
00777     {
00778         vVars->nSize = 0;
00779         Vec_IntPush( vVars, lit_neg(toLit(pFanin->Id)) );
00780         Vec_IntPush( vVars, toLit(pNode->Id) );
00781         RetValue = sat_solver_addclause( pSat, vVars->pArray, vVars->pArray + vVars->nSize );
00782         if ( !RetValue ) 
00783         {
00784             printf( "The CNF is trivially UNSAT.\n" );
00785             return 0;
00786         }
00787 
00788         vVars->nSize = 0;
00789         Vec_IntPush( vVars, toLit(pFanin->Id) );
00790         Vec_IntPush( vVars, lit_neg(toLit(pNode->Id)) );
00791         RetValue = sat_solver_addclause( pSat, vVars->pArray, vVars->pArray + vVars->nSize );
00792         if ( !RetValue ) 
00793         {
00794             printf( "The CNF is trivially UNSAT.\n" );
00795             return 0;
00796         }
00797     }
00798 
00799     vVars->nSize = 0;
00800     Vec_IntPush( vVars, toLit(pNode->Id) );
00801     RetValue = sat_solver_addclause( pSat, vVars->pArray, vVars->pArray + vVars->nSize );
00802     if ( !RetValue ) 
00803     {
00804         printf( "The CNF is trivially UNSAT.\n" );
00805         return 0;
00806     }
00807     return 1;
00808 }

int Abc_NtkClauseAnd ( sat_solver *  pSat,
Abc_Obj_t *  pNode,
Vec_Ptr_t *  vSuper,
Vec_Int_t *  vVars 
)

Function*************************************************************

Synopsis [Adds trivial clause.]

Description []

SideEffects []

SeeAlso []

Definition at line 214 of file abcSat.c.

00215 {
00216     int fComp1, Var, Var1, i;
00217 //printf( "Adding AND %d.  (%d)    %d\n", pNode->Id, vSuper->nSize+1, (int)pSat->sat_solver_stats.clauses );
00218 
00219     assert( !Abc_ObjIsComplement( pNode ) );
00220     assert( Abc_ObjIsNode( pNode ) );
00221 
00222 //    nVars = sat_solver_nvars(pSat);
00223     Var = (int)pNode->pCopy;
00224 //    Var = pNode->Id;
00225 
00226 //    assert( Var  < nVars ); 
00227     for ( i = 0; i < vSuper->nSize; i++ )
00228     {
00229         // get the predecessor nodes
00230         // get the complemented attributes of the nodes
00231         fComp1 = Abc_ObjIsComplement(vSuper->pArray[i]);
00232         // determine the variable numbers
00233         Var1 = (int)Abc_ObjRegular(vSuper->pArray[i])->pCopy;
00234 //        Var1 = (int)Abc_ObjRegular(vSuper->pArray[i])->Id;
00235 
00236         // check that the variables are in the SAT manager
00237 //        assert( Var1 < nVars );
00238 
00239         // suppose the AND-gate is A * B = C
00240         // add !A => !C   or   A + !C
00241     //  fprintf( pFile, "%d %d 0%c", Var1, -Var, 10 );
00242         vVars->nSize = 0;
00243         Vec_IntPush( vVars, toLitCond(Var1, fComp1) );
00244         Vec_IntPush( vVars, toLitCond(Var,  1     ) );
00245         if ( !sat_solver_addclause( pSat, vVars->pArray, vVars->pArray + vVars->nSize ) )
00246             return 0;
00247     }
00248 
00249     // add A & B => C   or   !A + !B + C
00250 //  fprintf( pFile, "%d %d %d 0%c", -Var1, -Var2, Var, 10 );
00251     vVars->nSize = 0;
00252     for ( i = 0; i < vSuper->nSize; i++ )
00253     {
00254         // get the predecessor nodes
00255         // get the complemented attributes of the nodes
00256         fComp1 = Abc_ObjIsComplement(vSuper->pArray[i]);
00257         // determine the variable numbers
00258         Var1 = (int)Abc_ObjRegular(vSuper->pArray[i])->pCopy;
00259 //        Var1 = (int)Abc_ObjRegular(vSuper->pArray[i])->Id;
00260         // add this variable to the array
00261         Vec_IntPush( vVars, toLitCond(Var1, !fComp1) );
00262     }
00263     Vec_IntPush( vVars, toLitCond(Var, 0) );
00264     return sat_solver_addclause( pSat, vVars->pArray, vVars->pArray + vVars->nSize );
00265 }

int Abc_NtkClauseMux ( sat_solver *  pSat,
Abc_Obj_t *  pNode,
Abc_Obj_t *  pNodeC,
Abc_Obj_t *  pNodeT,
Abc_Obj_t *  pNodeE,
Vec_Int_t *  vVars 
)

Function*************************************************************

Synopsis [Adds trivial clause.]

Description []

SideEffects []

SeeAlso []

Definition at line 278 of file abcSat.c.

00279 {
00280     int VarF, VarI, VarT, VarE, fCompT, fCompE;
00281 //printf( "Adding mux %d.         %d\n", pNode->Id, (int)pSat->sat_solver_stats.clauses );
00282 
00283     assert( !Abc_ObjIsComplement( pNode ) );
00284     assert( Abc_NodeIsMuxType( pNode ) );
00285     // get the variable numbers
00286     VarF = (int)pNode->pCopy;
00287     VarI = (int)pNodeC->pCopy;
00288     VarT = (int)Abc_ObjRegular(pNodeT)->pCopy;
00289     VarE = (int)Abc_ObjRegular(pNodeE)->pCopy;
00290 //    VarF = (int)pNode->Id;
00291 //    VarI = (int)pNodeC->Id;
00292 //    VarT = (int)Abc_ObjRegular(pNodeT)->Id;
00293 //    VarE = (int)Abc_ObjRegular(pNodeE)->Id;
00294 
00295     // get the complementation flags
00296     fCompT = Abc_ObjIsComplement(pNodeT);
00297     fCompE = Abc_ObjIsComplement(pNodeE);
00298 
00299     // f = ITE(i, t, e)
00300     // i' + t' + f
00301     // i' + t  + f'
00302     // i  + e' + f
00303     // i  + e  + f'
00304     // create four clauses
00305     vVars->nSize = 0;
00306     Vec_IntPush( vVars, toLitCond(VarI,  1) );
00307     Vec_IntPush( vVars, toLitCond(VarT,  1^fCompT) );
00308     Vec_IntPush( vVars, toLitCond(VarF,  0) );
00309     if ( !sat_solver_addclause( pSat, vVars->pArray, vVars->pArray + vVars->nSize ) )
00310         return 0;
00311     vVars->nSize = 0;
00312     Vec_IntPush( vVars, toLitCond(VarI,  1) );
00313     Vec_IntPush( vVars, toLitCond(VarT,  0^fCompT) );
00314     Vec_IntPush( vVars, toLitCond(VarF,  1) );
00315     if ( !sat_solver_addclause( pSat, vVars->pArray, vVars->pArray + vVars->nSize ) )
00316         return 0;
00317     vVars->nSize = 0;
00318     Vec_IntPush( vVars, toLitCond(VarI,  0) );
00319     Vec_IntPush( vVars, toLitCond(VarE,  1^fCompE) );
00320     Vec_IntPush( vVars, toLitCond(VarF,  0) );
00321     if ( !sat_solver_addclause( pSat, vVars->pArray, vVars->pArray + vVars->nSize ) )
00322         return 0;
00323     vVars->nSize = 0;
00324     Vec_IntPush( vVars, toLitCond(VarI,  0) );
00325     Vec_IntPush( vVars, toLitCond(VarE,  0^fCompE) );
00326     Vec_IntPush( vVars, toLitCond(VarF,  1) );
00327     if ( !sat_solver_addclause( pSat, vVars->pArray, vVars->pArray + vVars->nSize ) )
00328         return 0;
00329  
00330     if ( VarT == VarE )
00331     {
00332 //        assert( fCompT == !fCompE );
00333         return 1;
00334     }
00335 
00336     // two additional clauses
00337     // t' & e' -> f'       t  + e   + f'
00338     // t  & e  -> f        t' + e'  + f 
00339     vVars->nSize = 0;
00340     Vec_IntPush( vVars, toLitCond(VarT,  0^fCompT) );
00341     Vec_IntPush( vVars, toLitCond(VarE,  0^fCompE) );
00342     Vec_IntPush( vVars, toLitCond(VarF,  1) );
00343     if ( !sat_solver_addclause( pSat, vVars->pArray, vVars->pArray + vVars->nSize ) )
00344         return 0;
00345     vVars->nSize = 0;
00346     Vec_IntPush( vVars, toLitCond(VarT,  1^fCompT) );
00347     Vec_IntPush( vVars, toLitCond(VarE,  1^fCompE) );
00348     Vec_IntPush( vVars, toLitCond(VarF,  0) );
00349     return sat_solver_addclause( pSat, vVars->pArray, vVars->pArray + vVars->nSize );
00350 }

int Abc_NtkClauseTop ( sat_solver *  pSat,
Vec_Ptr_t *  vNodes,
Vec_Int_t *  vVars 
)

Function*************************************************************

Synopsis [Adds trivial clause.]

Description []

SideEffects []

SeeAlso []

Definition at line 191 of file abcSat.c.

00192 {
00193     Abc_Obj_t * pNode;
00194     int i;
00195 //printf( "Adding triv %d.         %d\n", Abc_ObjRegular(pNode)->Id, (int)pSat->sat_solver_stats.clauses );
00196     vVars->nSize = 0;
00197     Vec_PtrForEachEntry( vNodes, pNode, i )
00198         Vec_IntPush( vVars, toLitCond( (int)Abc_ObjRegular(pNode)->pCopy, Abc_ObjIsComplement(pNode) ) );
00199 //    Vec_IntPush( vVars, toLitCond( (int)Abc_ObjRegular(pNode)->Id, Abc_ObjIsComplement(pNode) ) );
00200     return sat_solver_addclause( pSat, vVars->pArray, vVars->pArray + vVars->nSize );
00201 }

int Abc_NtkClauseTriv ( sat_solver *  pSat,
Abc_Obj_t *  pNode,
Vec_Int_t *  vVars 
)

Function*************************************************************

Synopsis [Adds trivial clause.]

Description []

SideEffects []

SeeAlso []

Definition at line 171 of file abcSat.c.

00172 {
00173 //printf( "Adding triv %d.         %d\n", Abc_ObjRegular(pNode)->Id, (int)pSat->sat_solver_stats.clauses );
00174     vVars->nSize = 0;
00175     Vec_IntPush( vVars, toLitCond( (int)Abc_ObjRegular(pNode)->pCopy, Abc_ObjIsComplement(pNode) ) );
00176 //    Vec_IntPush( vVars, toLitCond( (int)Abc_ObjRegular(pNode)->Id, Abc_ObjIsComplement(pNode) ) );
00177     return sat_solver_addclause( pSat, vVars->pArray, vVars->pArray + vVars->nSize );
00178 }

void Abc_NtkCollectSupergate ( Abc_Obj_t *  pNode,
int  fStopAtMux,
Vec_Ptr_t *  vNodes 
)

Function*************************************************************

Synopsis [Returns the array of nodes to be combined into one multi-input AND-gate.]

Description []

SideEffects []

SeeAlso []

Definition at line 410 of file abcSat.c.

00411 {
00412     int RetValue, i;
00413     assert( !Abc_ObjIsComplement(pNode) );
00414     // collect the nodes in the implication supergate
00415     Vec_PtrClear( vNodes );
00416     RetValue = Abc_NtkCollectSupergate_rec( pNode, vNodes, 1, fStopAtMux );
00417     assert( vNodes->nSize > 1 );
00418     // unmark the visited nodes
00419     for ( i = 0; i < vNodes->nSize; i++ )
00420         Abc_ObjRegular((Abc_Obj_t *)vNodes->pArray[i])->fMarkB = 0;
00421     // if we found the node and its complement in the same implication supergate, 
00422     // return empty set of nodes (meaning that we should use constant-0 node)
00423     if ( RetValue == -1 )
00424         vNodes->nSize = 0;
00425 }

int Abc_NtkCollectSupergate_rec ( Abc_Obj_t *  pNode,
Vec_Ptr_t *  vSuper,
int  fFirst,
int  fStopAtMux 
)

Function*************************************************************

Synopsis [Returns the array of nodes to be combined into one multi-input AND-gate.]

Description []

SideEffects []

SeeAlso []

Definition at line 363 of file abcSat.c.

00364 {
00365     int RetValue1, RetValue2, i;
00366     // check if the node is visited
00367     if ( Abc_ObjRegular(pNode)->fMarkB )
00368     {
00369         // check if the node occurs in the same polarity
00370         for ( i = 0; i < vSuper->nSize; i++ )
00371             if ( vSuper->pArray[i] == pNode )
00372                 return 1;
00373         // check if the node is present in the opposite polarity
00374         for ( i = 0; i < vSuper->nSize; i++ )
00375             if ( vSuper->pArray[i] == Abc_ObjNot(pNode) )
00376                 return -1;
00377         assert( 0 );
00378         return 0;
00379     }
00380     // if the new node is complemented or a PI, another gate begins
00381     if ( !fFirst )
00382     if ( Abc_ObjIsComplement(pNode) || !Abc_ObjIsNode(pNode) || Abc_ObjFanoutNum(pNode) > 1 || fStopAtMux && Abc_NodeIsMuxType(pNode) )
00383     {
00384         Vec_PtrPush( vSuper, pNode );
00385         Abc_ObjRegular(pNode)->fMarkB = 1;
00386         return 0;
00387     }
00388     assert( !Abc_ObjIsComplement(pNode) );
00389     assert( Abc_ObjIsNode(pNode) );
00390     // go through the branches
00391     RetValue1 = Abc_NtkCollectSupergate_rec( Abc_ObjChild0(pNode), vSuper, 0, fStopAtMux );
00392     RetValue2 = Abc_NtkCollectSupergate_rec( Abc_ObjChild1(pNode), vSuper, 0, fStopAtMux );
00393     if ( RetValue1 == -1 || RetValue2 == -1 )
00394         return -1;
00395     // return 1 if at least one branch has a duplicate
00396     return RetValue1 || RetValue2;
00397 }

Vec_Int_t * Abc_NtkGetCiSatVarNums ( Abc_Ntk_t *  pNtk  ) 

Function*************************************************************

Synopsis [Returns the array of CI IDs.]

Description []

SideEffects []

SeeAlso []

Definition at line 147 of file abcSat.c.

00148 {
00149     Vec_Int_t * vCiIds;
00150     Abc_Obj_t * pObj;
00151     int i;
00152     vCiIds = Vec_IntAlloc( Abc_NtkCiNum(pNtk) );
00153     Abc_NtkForEachCi( pNtk, pObj, i )
00154         Vec_IntPush( vCiIds, (int)pObj->pCopy );
00155     return vCiIds;
00156 }

int Abc_NtkMiterSat ( Abc_Ntk_t *  pNtk,
sint64  nConfLimit,
sint64  nInsLimit,
int  fVerbose,
sint64 *  pNumConfs,
sint64 *  pNumInspects 
)

FUNCTION DEFINITIONS ///Function*************************************************************

Synopsis [Attempts to solve the miter using an internal SAT sat_solver.]

Description [Returns -1 if timed out; 0 if SAT; 1 if UNSAT.]

SideEffects []

SeeAlso []

Definition at line 47 of file abcSat.c.

00048 {
00049     sat_solver * pSat;
00050     lbool   status;
00051     int RetValue, clk;
00052  
00053     if ( pNumConfs )
00054         *pNumConfs = 0;
00055     if ( pNumInspects )
00056         *pNumInspects = 0;
00057 
00058     assert( Abc_NtkLatchNum(pNtk) == 0 );
00059 
00060 //    if ( Abc_NtkPoNum(pNtk) > 1 )
00061 //        fprintf( stdout, "Warning: The miter has %d outputs. SAT will try to prove all of them.\n", Abc_NtkPoNum(pNtk) );
00062 
00063     // load clauses into the sat_solver
00064     clk = clock();
00065     pSat = Abc_NtkMiterSatCreate( pNtk, 0 );
00066     if ( pSat == NULL )
00067         return 1;
00068 //printf( "%d \n", pSat->clauses.size );
00069 //sat_solver_delete( pSat );
00070 //return 1;
00071 
00072 //    printf( "Created SAT problem with %d variable and %d clauses. ", sat_solver_nvars(pSat), sat_solver_nclauses(pSat) );
00073 //    PRT( "Time", clock() - clk );
00074 
00075     // simplify the problem
00076     clk = clock();
00077     status = sat_solver_simplify(pSat);
00078 //    printf( "Simplified the problem to %d variables and %d clauses. ", sat_solver_nvars(pSat), sat_solver_nclauses(pSat) );
00079 //    PRT( "Time", clock() - clk );
00080     if ( status == 0 )
00081     {
00082         sat_solver_delete( pSat );
00083 //        printf( "The problem is UNSATISFIABLE after simplification.\n" );
00084         return 1;
00085     }
00086 
00087     // solve the miter
00088     clk = clock();
00089     if ( fVerbose )
00090         pSat->verbosity = 1;
00091     status = sat_solver_solve( pSat, NULL, NULL, (sint64)nConfLimit, (sint64)nInsLimit, (sint64)0, (sint64)0 );
00092     if ( status == l_Undef )
00093     {
00094 //        printf( "The problem timed out.\n" );
00095         RetValue = -1;
00096     }
00097     else if ( status == l_True )
00098     {
00099 //        printf( "The problem is SATISFIABLE.\n" );
00100         RetValue = 0;
00101     }
00102     else if ( status == l_False )
00103     {
00104 //        printf( "The problem is UNSATISFIABLE.\n" );
00105         RetValue = 1;
00106     }
00107     else
00108         assert( 0 );
00109 //    PRT( "SAT sat_solver time", clock() - clk );
00110 //    printf( "The number of conflicts = %d.\n", (int)pSat->sat_solver_stats.conflicts );
00111 
00112     // if the problem is SAT, get the counterexample
00113     if ( status == l_True )
00114     {
00115 //        Vec_Int_t * vCiIds = Abc_NtkGetCiIds( pNtk );
00116         Vec_Int_t * vCiIds = Abc_NtkGetCiSatVarNums( pNtk );
00117         pNtk->pModel = Sat_SolverGetModel( pSat, vCiIds->pArray, vCiIds->nSize );
00118         Vec_IntFree( vCiIds );
00119     }
00120     // free the sat_solver
00121     if ( fVerbose )
00122         Sat_SolverPrintStats( stdout, pSat );
00123 
00124     if ( pNumConfs )
00125         *pNumConfs = (int)pSat->stats.conflicts;
00126     if ( pNumInspects )
00127         *pNumInspects = (int)pSat->stats.inspects;
00128 
00129 sat_solver_store_write( pSat, "trace.cnf" );
00130 sat_solver_store_free( pSat );
00131 
00132     sat_solver_delete( pSat );
00133     return RetValue;
00134 }

void* Abc_NtkMiterSatCreate ( Abc_Ntk_t *  pNtk,
int  fAllPrimes 
)

Function*************************************************************

Synopsis [Sets up the SAT sat_solver.]

Description []

SideEffects []

SeeAlso []

Definition at line 614 of file abcSat.c.

00615 {
00616     sat_solver * pSat;
00617     Abc_Obj_t * pNode;
00618     int RetValue, i, clk = clock();
00619 
00620     assert( Abc_NtkIsStrash(pNtk) || Abc_NtkIsBddLogic(pNtk) );
00621     if ( Abc_NtkIsBddLogic(pNtk) )
00622         return Abc_NtkMiterSatCreateLogic(pNtk, fAllPrimes);
00623 
00624     nMuxes = 0;
00625     pSat = sat_solver_new();
00626 //sat_solver_store_alloc( pSat );
00627     RetValue = Abc_NtkMiterSatCreateInt( pSat, pNtk );
00628 sat_solver_store_mark_roots( pSat );
00629 
00630     Abc_NtkForEachObj( pNtk, pNode, i )
00631         pNode->fMarkA = 0;
00632 //    ASat_SolverWriteDimacs( pSat, "temp_sat.cnf", NULL, NULL, 1 );
00633     if ( RetValue == 0 )
00634     {
00635         sat_solver_delete(pSat);
00636         return NULL;
00637     }
00638 //    printf( "Ands = %6d.  Muxes = %6d (%5.2f %%).  ", Abc_NtkNodeNum(pNtk), nMuxes, 300.0*nMuxes/Abc_NtkNodeNum(pNtk) );
00639 //    PRT( "Creating sat_solver", clock() - clk );
00640     return pSat;
00641 }

int Abc_NtkMiterSatCreateInt ( sat_solver *  pSat,
Abc_Ntk_t *  pNtk 
)

Function*************************************************************

Synopsis [Sets up the SAT sat_solver.]

Description []

SideEffects []

SeeAlso []

Definition at line 459 of file abcSat.c.

00460 {
00461     Abc_Obj_t * pNode, * pFanin, * pNodeC, * pNodeT, * pNodeE;
00462     Vec_Ptr_t * vNodes, * vSuper;
00463     Vec_Int_t * vVars;
00464     int i, k, fUseMuxes = 1;
00465     int clk1 = clock();
00466 //    int fOrderCiVarsFirst = 0;
00467     int nLevelsMax = Abc_AigLevel(pNtk);
00468     int RetValue = 0;
00469 
00470     assert( Abc_NtkIsStrash(pNtk) );
00471 
00472     // clean the CI node pointers
00473     Abc_NtkForEachCi( pNtk, pNode, i )
00474         pNode->pCopy = NULL;
00475 
00476     // start the data structures
00477     vNodes  = Vec_PtrAlloc( 1000 );   // the nodes corresponding to vars in the sat_solver
00478     vSuper  = Vec_PtrAlloc( 100 );    // the nodes belonging to the given implication supergate
00479     vVars   = Vec_IntAlloc( 100 );    // the temporary array for variables in the clause
00480 
00481     // add the clause for the constant node
00482     pNode = Abc_AigConst1(pNtk);
00483     pNode->fMarkA = 1;
00484     pNode->pCopy = (Abc_Obj_t *)vNodes->nSize;
00485     Vec_PtrPush( vNodes, pNode );
00486     Abc_NtkClauseTriv( pSat, pNode, vVars );
00487 /*
00488     // add the PI variables first
00489     Abc_NtkForEachCi( pNtk, pNode, i )
00490     {
00491         pNode->fMarkA = 1;
00492         pNode->pCopy = (Abc_Obj_t *)vNodes->nSize;
00493         Vec_PtrPush( vNodes, pNode );
00494     }
00495 */
00496     // collect the nodes that need clauses and top-level assignments
00497     Vec_PtrClear( vSuper );
00498     Abc_NtkForEachCo( pNtk, pNode, i )
00499     {
00500         // get the fanin
00501         pFanin = Abc_ObjFanin0(pNode);
00502         // create the node's variable
00503         if ( pFanin->fMarkA == 0 )
00504         {
00505             pFanin->fMarkA = 1;
00506             pFanin->pCopy = (Abc_Obj_t *)vNodes->nSize;
00507             Vec_PtrPush( vNodes, pFanin );
00508         }
00509         // add the trivial clause
00510         Vec_PtrPush( vSuper, Abc_ObjChild0(pNode) );
00511     }
00512     if ( !Abc_NtkClauseTop( pSat, vSuper, vVars ) )
00513         goto Quits;
00514 
00515 
00516     // add the clauses
00517     Vec_PtrForEachEntry( vNodes, pNode, i )
00518     {
00519         assert( !Abc_ObjIsComplement(pNode) );
00520         if ( !Abc_AigNodeIsAnd(pNode) )
00521             continue;
00522 //printf( "%d ", pNode->Id );
00523 
00524         // add the clauses
00525         if ( fUseMuxes && Abc_NodeIsMuxType(pNode) )
00526         {
00527             nMuxes++;
00528 
00529             pNodeC = Abc_NodeRecognizeMux( pNode, &pNodeT, &pNodeE );
00530             Vec_PtrClear( vSuper );
00531             Vec_PtrPush( vSuper, pNodeC );
00532             Vec_PtrPush( vSuper, pNodeT );
00533             Vec_PtrPush( vSuper, pNodeE );
00534             // add the fanin nodes to explore
00535             Vec_PtrForEachEntry( vSuper, pFanin, k )
00536             {
00537                 pFanin = Abc_ObjRegular(pFanin);
00538                 if ( pFanin->fMarkA == 0 )
00539                 {
00540                     pFanin->fMarkA = 1;
00541                     pFanin->pCopy = (Abc_Obj_t *)vNodes->nSize;
00542                     Vec_PtrPush( vNodes, pFanin );
00543                 }
00544             }
00545             // add the clauses
00546             if ( !Abc_NtkClauseMux( pSat, pNode, pNodeC, pNodeT, pNodeE, vVars ) )
00547                 goto Quits;
00548         }
00549         else
00550         {
00551             // get the supergate
00552             Abc_NtkCollectSupergate( pNode, fUseMuxes, vSuper );
00553             // add the fanin nodes to explore
00554             Vec_PtrForEachEntry( vSuper, pFanin, k )
00555             {
00556                 pFanin = Abc_ObjRegular(pFanin);
00557                 if ( pFanin->fMarkA == 0 )
00558                 {
00559                     pFanin->fMarkA = 1;
00560                     pFanin->pCopy = (Abc_Obj_t *)vNodes->nSize;
00561                     Vec_PtrPush( vNodes, pFanin );
00562                 }
00563             }
00564             // add the clauses
00565             if ( vSuper->nSize == 0 )
00566             {
00567                 if ( !Abc_NtkClauseTriv( pSat, Abc_ObjNot(pNode), vVars ) )
00568 //                if ( !Abc_NtkClauseTriv( pSat, pNode, vVars ) )
00569                     goto Quits;
00570             }
00571             else
00572             {
00573                 if ( !Abc_NtkClauseAnd( pSat, pNode, vSuper, vVars ) )
00574                     goto Quits;
00575             }
00576         }
00577     }
00578 /*
00579     // set preferred variables
00580     if ( fOrderCiVarsFirst )
00581     {
00582         int * pPrefVars = ALLOC( int, Abc_NtkCiNum(pNtk) );
00583         int nVars = 0;
00584         Abc_NtkForEachCi( pNtk, pNode, i )
00585         {
00586             if ( pNode->fMarkA == 0 )
00587                 continue;
00588             pPrefVars[nVars++] = (int)pNode->pCopy;
00589         }
00590         nVars = ABC_MIN( nVars, 10 );
00591         ASat_SolverSetPrefVars( pSat, pPrefVars, nVars );
00592     }
00593 */
00594     RetValue = 1;
00595 Quits :
00596     // delete
00597     Vec_IntFree( vVars );
00598     Vec_PtrFree( vNodes );
00599     Vec_PtrFree( vSuper );
00600     return RetValue;
00601 }

sat_solver * Abc_NtkMiterSatCreateLogic ( Abc_Ntk_t *  pNtk,
int  fAllPrimes 
) [static]

CFile****************************************************************

FileName [abcSat.c]

SystemName [ABC: Logic synthesis and verification system.]

PackageName [Network and node package.]

Synopsis [Procedures to solve the miter using the internal SAT sat_solver.]

Author [Alan Mishchenko]

Affiliation [UC Berkeley]

Date [Ver. 1.0. Started - June 20, 2005.]

Revision [

Id
abcSat.c,v 1.00 2005/06/20 00:00:00 alanmi Exp

] DECLARATIONS ///

Function*************************************************************

Synopsis [Sets up the SAT sat_solver.]

Description []

SideEffects []

SeeAlso []

Definition at line 821 of file abcSat.c.

00822 {
00823     sat_solver * pSat;
00824     Extra_MmFlex_t * pMmFlex;
00825     Abc_Obj_t * pNode;
00826     Vec_Str_t * vCube;
00827     Vec_Int_t * vVars;
00828     char * pSop0, * pSop1;
00829     int i;
00830 
00831     assert( Abc_NtkIsBddLogic(pNtk) );
00832 
00833     // transfer the IDs to the copy field
00834     Abc_NtkForEachPi( pNtk, pNode, i )
00835         pNode->pCopy = (void *)pNode->Id;
00836 
00837     // start the data structures
00838     pSat    = sat_solver_new();
00839 sat_solver_store_alloc( pSat );
00840     pMmFlex = Extra_MmFlexStart();
00841     vCube   = Vec_StrAlloc( 100 );
00842     vVars   = Vec_IntAlloc( 100 );
00843 
00844     // add clauses for each internal nodes
00845     Abc_NtkForEachNode( pNtk, pNode, i )
00846     {
00847         // derive SOPs for both phases of the node
00848         Abc_NodeBddToCnf( pNode, pMmFlex, vCube, fAllPrimes, &pSop0, &pSop1 );
00849         // add the clauses to the sat_solver
00850         if ( !Abc_NodeAddClauses( pSat, pSop0, pSop1, pNode, vVars ) )
00851         {
00852             sat_solver_delete( pSat );
00853             pSat = NULL;
00854             goto finish;
00855         }
00856     }
00857     // add clauses for each PO
00858     Abc_NtkForEachPo( pNtk, pNode, i )
00859     {
00860         if ( !Abc_NodeAddClausesTop( pSat, pNode, vVars ) )
00861         {
00862             sat_solver_delete( pSat );
00863             pSat = NULL;
00864             goto finish;
00865         }
00866     }
00867 sat_solver_store_mark_roots( pSat );
00868 
00869 finish:
00870     // delete
00871     Vec_StrFree( vCube );
00872     Vec_IntFree( vVars );
00873     Extra_MmFlexStop( pMmFlex );
00874     return pSat;
00875 }

int Abc_NtkNodeFactor ( Abc_Obj_t *  pObj,
int  nLevelMax 
)

Function*************************************************************

Synopsis [Computes the factor of the node.]

Description []

SideEffects []

SeeAlso []

Definition at line 439 of file abcSat.c.

00440 {
00441 //  nLevelMax = ((nLevelMax)/2)*3;
00442     assert( (int)pObj->Level <= nLevelMax );
00443 //    return (int)(100000000.0 * pow(0.999, nLevelMax - pObj->Level));
00444     return (int)(100000000.0 * (1 + 0.01 * pObj->Level));
00445 //    return (int)(100000000.0 / ((nLevelMax)/2)*3 - pObj->Level);
00446 }

Variable Documentation

nMuxes [static]

Definition at line 30 of file abcSat.c.

Generated on Tue Jan 5 12:18:42 2010 for abc70930 by  doxygen 1.6.1