Local Linear Smoothing (LLS)
Matlab functions implementing non-parametric local linear smoothing (LLS) for
one-dimensional curve fitting: yi = f(xi) +
ei for i = 1, 2, ..., n. The toolbox contains: (i) the usual LLS estimator, see e.g. [1]; (ii) a
jump-preserving (two-sided) LLS estimator proposed in [2]; (iii) a
modified version of the two-sided LLS proposed in [3].
I/O:
Input: predictor vector x, response vector y, kernel option (see the code comments for details), bandwidth h,
and a set of points z of x in [0,1] whose responses are to be
predicted by the fitted curve.
Output: predicted values of f(z).
Example:
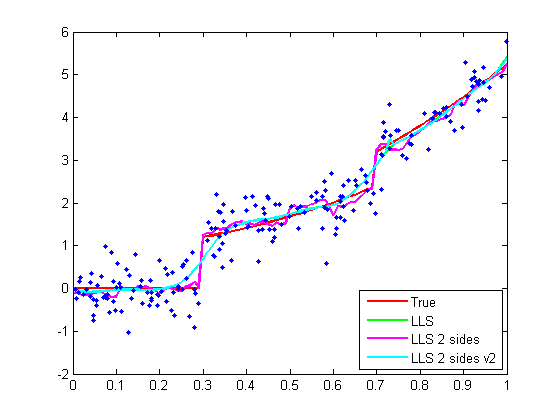
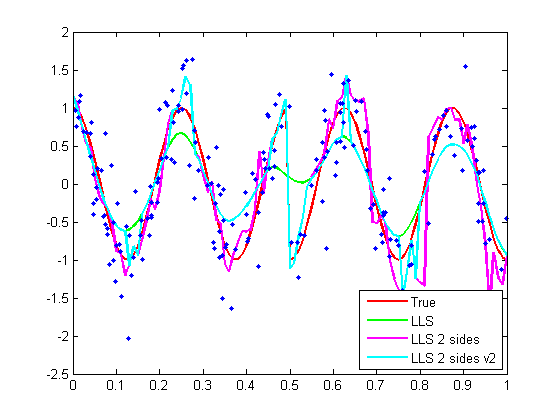
200 data are simulated for each of three mean functions (see the
function reg_mean_fun.m). The fitted curves and data are shown below.
Bandwidth and other related parameters are determined by 5-fold
cross-validation.
- True mean functions are shown in red.
- Usual LLS curves are in green. [1]
- Two-sided jump-preserving LLS curves are in magenta. [2]
- A modified version of the two-sided LLS curves (to stabilize the noise in
continuous regions) are shown in cyan. [3]
Several things can be observed in these
examples:
1. Usual LLS is not consistent at jump points.
2. The two-sided LLS is jump-preserving; however, it is pretty noisy in
continuous regions of true mean functions.
3. The modified version of the two-sided LLS procedure can accurately detect
jumps and reduce the noise of two-sided LLS in continuous regions.

Download .m files:
local_linear_smoothing.zip
Remark:
1. All points of x are normalized in the interval [0,1].
2. This toolbox is
self-contained and therefore can be run standalone. Extract the zipped file and
then run demo to reproduce above plots and get a flavor!
References:
[1] Fan (1993) Local linear regression smoothers and their minimax efficiencies.
Annals of Statistics.
[2] Qiu (2003) A jump-preserving curve fitting procedure based on local
piecewise linear kernel estimation. Journal of Nonparametric Statistics.
[3] Gijbels, Lambert, Qiu (2007) Jump-preserving regression and smoothing using
local linear fitting: a compromise. Annals of the Institute of Statistical
Mathematics.
Back to
Homepage


