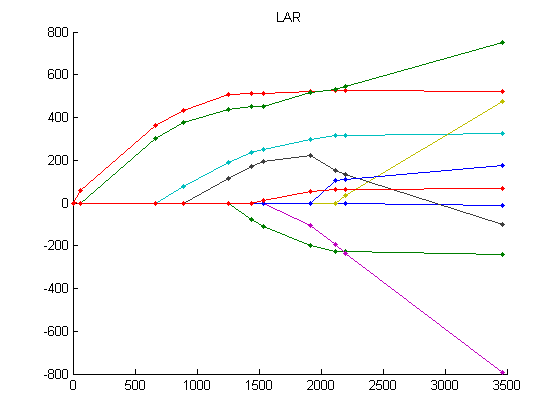
LARS and Lasso whole paths for the diabetes data set used in [1].

Least Angle Regression (LARS)
Matlab code for the LARS algorithm [1], which computes the whole optimal path, by a homotopy approach, for the LAR and Lasso problem in constrained form.
I/O:
Input: a design matrix X, a response vector Y, option = lar or lasso, and
an (optional) constraint parameter.
Output: the estimated coefficient vector and its support index, the
estimated mean vector, and the current correlation and its maximal magnitude in
the final step, and the history of step lengths during the LARS iterations. For
details, see the function documentation.
Example:
LARS and Lasso whole paths for the
diabetes data set used in [1].


Remark: There are two options using LARS function: one is standardized data (default) and the other is non-standardized. Standardized version of LARS centers Y and normalizes each columns of X to zero-mean and unit Euclidean length. To switch from standardized version to non-standardized one, simply setting the function parameter standardize = false.
Download .m files:
LARS.m
References:
[1] Efron Brad, et al. (2004) Least angle regression. Annals of Statistics,
32(2):407-499.