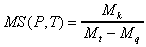Abstract

1. Introduction

2. Strong Mutation Testing

(1)

where	P is the test program;
	T is the set of test data;
	Mk is the number of mutants killed by T;
	Mt is the total number of mutants generated for the program;
	Mq is the number of equivalent mutants for the program.

A set of test data is mutation-adequate if its mutation score is 100%.

2.1 Mutation Operators

Table1. Mothra Mutation Operators

Type	Description
aar	array for array replacement
abs	absolute value insertion
acr	array constant replacement
aor	arithmetic operator replacement
asr	array for variable replacement
car	constant for array replacement
cnr	comparable array replacement
csr	constant for scalar replacement
der	DO statement end replacement
lcr	logical connector replacement
ror	relational operator replacement
sar	scalar for array replacement
scr	scalar for constant replacement
svr	scalar variable replacement
crp	constant replacement
dsa	data statement alterations
glr	goto label replacement
rsr	return statement replacement
san	statement analysis
sdl	statement deletion
src	source constant replacement
uoi	unary operation insertion

Consider an example used in [4] and [6], which determines the index of the first occurrence of a maximum element in a single-dimensioned array. The C version of the program is given in Fig 1.

int max(int* input, int size)
{
int j, result;
result = 0;
for (j =1; j < size; j++) {
if (input[j] > input[result])
result = j;
}
return result;
}

Fig 1. C Program "max"

Test sets for the original "max" program are shown in Table 2.

Table 2. Initial Test Sets for "max"

Data Set #	input(0)	input(1)	input(2)	Expected result
Data set 1	1	2	3	3
Data set 2	3	1	2	1
Data set 3	1	3	2	2

A relational mutation operator (ror) is applied to the "max" program. The resulting mutant is shown in Fig 2.

int max(int* input, int size)
{
int j, result;
result = input[0];
for (j =1; j < size; j++) {
if (input[j] >= input[result])
result = j;
}
return result;
}

Fig 2. C Program "max" with Relational Operator Replacement.

The test set in Table 2 is applied to the rationally mutated program. The result obtained are stated in Table 3 below.

Table 3. Outputs Obtained from Mutated "max" Using Initial Test Data.

Data Set #	input(0)	input(1)	input(2)	Output of mutated "max"	Expected result
Data set 1	1	2	3	3	3
Data set 2	3	1	2	1	1
Data set 3	1	3	2	2	2

From Table 3, the initial set of test data cannot kill the mutant. The set of test data is enhanced (Table 4) to kill the live mutant.

Table 4. An Enhanced Test Set for "max"

Data Set #	input(0)	input(1)	input(2)	Output of mutated "max"	Expected result
Data set 1	1	2	3	3	3
Data set 2	3	1	2	1	1
Data set 3	1	3	2	2	2
Data set 4	1	2	2	3	2

A functionally equivalent mutant of "max" is illustrated in Fig 3. The equivalent mutant cannot be killed by any set of data.

int max(int* input, int size)
{
int j, result;
result = input[0];
for (j =0; j < size; j++) {
if (input[j] > input[result])
result = j;
}
return result;
}

Fig 3. An Equivalent Mutant (CRP) to "max".

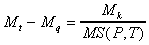2.2 The Cost of Strong Mutation Testing

(2)

Since the number of live mutants in an example is usually low, M_t - M_q gives a good indication of the number of mutants generated. Thus, the 11 line BUBBLE has about three hundred mutants generated; the 29 line CALENDAR has around 2600 mutants; FIND has about 950 mutants; GCD has around 4750 mutants. Each mutant must be executed at least once; many are executed more than once. Thus, the number of computations for a test set is huge. Methods have been proposed to improve the performance of strong mutation testing. Mathur [10] suggested the use of parallel computers. He had attempted to exploit difference architectures such as vector machines, SIMD machines, and MIMD machines. Programs that have fast compile time compared to their execution time benefit from the use of parallel machines. A different approach, known as Compiler Integrated testing (CIT), integrates testing methods into a compiler. This approach takes advantage of the compiler's ability to generate mutants efficiently, thereby, increasing the parallel machine's utilization. Besides using better hardware, variations of mutation testing have been introduced to the reduce the number of mutants generated while maintaining a reasonably good test coverage. Three better known variations of strong mutation testing are weak mutation, firm mutation, and selective mutation.

2.3 Effectiveness of Strong Mutation Testing

Mutation testing has been empirically found to be one of the most effective testing methods in finding faults: it is effective in finding faults of omissions and faults of commissions [7]. The notion of effectiveness in testing has been defined in several ways. Goodenough and Gerhart defined effectiveness in terms of reliability and validity. A test is reliable for an error if its use is guaranteed to detect the presence of the error [8]. According to Weyuker and Ostrand [9], a test set is effective if the test set reveals all errors that are represented by the difference between a function and a mutated version of the function. Weyuker and Ostrand's definition of effectiveness can be measured by mutation scores.

Table 5 and Table 6 summarize the averaged results of strong mutation testing done in [4] and [5] respectively. Data were collected over five different test sets. The tables describe the number of test cases generated, the number of mutants killed, and the mutation score of various programs.

Table 5. Results of Tests Done in [4]					Table 6. Results of Tests Done in [5]
Program	Number of Test Cases	Number of Mutants killed	Mutation Score		Program	Number of Test Cases	Number of Mutants killed	Mutation Score
BUBBLE	6.4	304	1.00		BANKER	57.4	2765	1.000
CALENAR	83.8	2624	.95		BUBBLE	7.2	338	1.000
FIND	11.6	953	.99		CALENDAR	50.0	3010	1.000
GCD	65	4747	.99		EUCLID	3.8	196	1.000
TRITYP	107.2	959	.997		FIND	14.6	1019	0.9994
					INSERT	3.8	460	1.000
					MID	25.2	183	1.000
					QUAD	12.2	359	1.000
					TRITYP	44.6	950	0.9998
					WARSHALL	7.2	305	1.000

Observing the results in Table 5 and 6, one can conclude that strong mutation testing indeed is effective: the mutation scores of various programs range from 95% to 100%. The test cases generated using strong mutation testing can kill almost all of the non-equivalent mutants.

3. Weak Mutation Testing

Strong mutation testing is a powerful unit-testing technique, but it suffers from expensive computational cost. Howden [7] proposed a modification known as weak mutation testing. Weak mutation testing is computationally more efficient because it provides a less stringent test. Weak mutation testing can be described as follows:

Given a program P and a simple component C of P. C' is a mutated version of C, and P' is the mutant of P containing C'. A test set is adequate for weak mutation testing if it causes C' to compute a different value from the value computed by C on at least one of execution of C'. Note that even though C' may produce a different value from C, P' may still produce the result as P. Weak mutation requires a less stringent test set because it only requires C and C' to produce different outputs [7].

3.1 Definition of a Component

When Howden first proposed weak mutation testing, he did not define what a component is. Instead, he listed five types of program components that he considered:

1. variable reference
2. variable assignment
3. arithmetic expression
4. relational expression
5. boolean expression

Offutt and Lee [2], later in their Leonardo weak mutation system, defined component as the location of the program at which the states of the original and the mutated program are compared. They varied the location for comparison in order to determine the best comparison point. Using their terminology, the variants that they used are:

1. EXpression-WEAK/1. EX-WEAK/1 compares the states after the execution of the innermost expression with the mutation operator.
2. STatement-WEAK/1. ST-WEAK/1 compares the state after the first execution of the mutated statement.
3. Basic-Block-WEAK/1. BB-WEAK/1 compares the state after the first execution of the basic mutated block.
4. Basic-Block-WEAK/N. BB-WEAK/N compares the state after the Nth execution of the basic mutated block.

Lets return to the "max" example. "Max" with a constant for array replacement (CAR) mutation operator applied is shown in Fig 4.

1	int max(int* input, int size)
2	{
3	int j, result;
4	result = input[0];
5	for (j =1; j < size; j++) {
6	if (input[j] > result)
7	result = j;
8	}
9	return result;
10	}

Fig 4. C Program "max" with a Constant for Array Replacement

The CAR mutation operator changes the array element, input[result], to a constant, result, in line 6. Under EX-WEAK/1, the value of the expression (result) will be compared with the expression (input[result]). Under ST-WEAK/1, the predicate (input[j] > result) will be compared with (input[j] > input[result]). Under BB-WEAK/1, the program state at line 8 will be compared. Under BB-WEAK/N, the program state will be compared every time line 8 is reached. The points of comparison for the four variants are shown in Fig. 5.

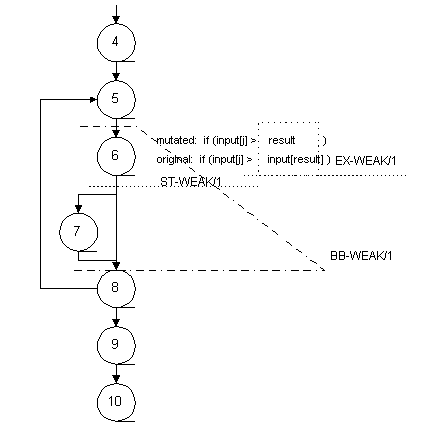
Fig 5. Locations of Comparisons for Weak Mutation Variants

3.2 The Cost of Weak Mutation Testing

Table7. Number of Test Cases Generated by Weak Mutation Testing

Program	EX-WEAK/1	ST-WEAK/1	BB-WEAK/1	BB-WEAK/N
BUB	7	11	10	7
CAL	13	25	25	20
EUCLID	4	5	4	3
FIND	11	15	14	7
INSERT	5	7	7	4
PAT	8	11	10	12
WARSHALL	5	9	9	3

Comparing the values above with the ones from Table 5 and Table 6, the number of test cases generated for weak mutation testing decrease drastically. Thus, the cost of weak mutation testing is less than that of strong mutation testing.

3.3 Effectiveness of Weak Mutation Testing

According to Offutt and Lee [2], if the same set of test data is applied to both strong mutation testing and weak mutation testing, the adequate score of weak mutation testing will usually be as high as the adequate score of strong mutation testing. Weak mutation scores better than strong mutation most of the time. It is not because weak mutation is better, but weak mutation requires a less stringent test. Thus, the test set created by weak mutation is weaker than the ones by strong mutation. In one of Offutt and Lee's experiment, they created 100% adequate test sets for all four variants of weak mutation testing on 11 programs. The 100% adequate test sets were then applied to strong mutation testing. The resulting adequate scores are compared and shown in Fig 6.

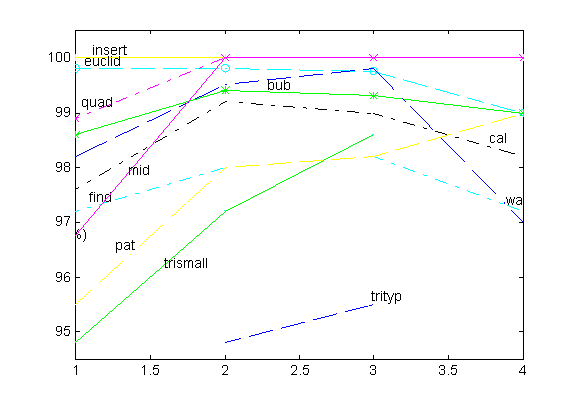
Fig 6. Strong Mutation Score on Weak Mutation Test Sets [2]

As seen from Fig 6, test sets from EX-WEAK/1 tend to be weaker than those of the other variants. Test sets from ST-WEAK and BB-WEAJ/1 tend to be the strongest, giving strong mutation scores ranged from 94.8% to 100%. The test set for BB-WEAK/N performs better than BB-WEAK/1 in only one case. That is, the state of the mutated block does not change at the end of the first iteration, but it changes at least once in the next N-1 iteration. The 100% adequate weak mutation test sets do not give rise to 100% strong mutation test scores in most of the cases. Even though test sets from weak mutation testing may cause a mutated program to produce different values for a component, the program may still output a correct result. Therefore, test sets from weak mutation testing are effective only at the component level.

4. Firm Mutation Testing

Firm mutation testing is actually an extension to weak mutation testing. In weak mutation testing, the state of the program is compared after every execution of the component. In strong mutation testing, the output of the program is compared at the end of the program execution. Firm mutation compares the state of the program at some time slice of the program execution that is at least as long as the execution of the mutated statement [13]. The exact component for comparison in firm mutation will be of the user's choices. As described by Woodward and Halewood [13], firm mutation offers users a great degree of control in the following ways:

1. code selection. The user-selectable section of a program can be any program structure or sequence of structures. The possible code selections for the "max" example are shown in Table 8.

   Table 8. Possible Code Selections for "max"

   1.	j
   2.	if (j > input[result]) result = j;
   3.	for (j =1; j < size; j++) { if (input[j] > input[result]) result = j; }
   4.	result = 0; for (j =1; j < size; j++) { if (input[j] > input[result]) result = j; }
   5.	int max(int* input, int size) { int j, result; result = 0; for (j =1; j < size; j++) { if (input[j] > input[result]) result = j; } return result; }

2. result comparison. Any object that is either defined, or referenced and defined in the selected region, can be used for result comparison [13]. Table 9 shows some of the possible variables for each possible code selection shown in Table 8 that can be used for comparisons.

   Table 9. Possible Result Comparisons for "max".

   Code selection #	Possible result comparisons
   1	j
   2	result,input[result],j
   3	result,input[result],input[j],j,size
   4	result,input[result],input[j],j,size
   5	result,input[result],input[j],j,input,size

3. mutant operator selection. Any mutation operator specified in Table 1 can be applied to the selection of codes.

The biggest advantage of firm mutation testing is that users can specify the part of codes to be tested, the variables for comparisons, and the mutant operator to be used in the test. That is, the users have great control in determining what criteria needed to kill a mutant.

Some combinations of choices for firm mutation testing are listed in Table 10.

Table 10. Possible Combinations of Code Selections, Result Comparisons, and Mutation Operators

	Code Selection	Result Comparison	Mutation Operator	Effects
1	for (j =1; j < size; j++) { if (input[j] > input[result]) result = j; }	result	ACR on j: result = j; --> result = input[j];	Compare the value of "result" at the end of the for loop execution
2	if (j > input[result]) result = j;	result	ROR on >: > --> <	compare the value of "result" after every execution of the result = j; statement

Firm mutation testing is computation less expensive than strong mutation testing since it can select a part of the program for execution. It gives more control to users since it allows users to specify the section of codes to be tested, the point of comparison, and the type of mutation. If the changes made to the program can be reversed in the program execution, several test cases can be combined in to one single test. More computational expenses can be saved.

5. Selective Mutation Testing

5.1 The Cost of Selective Mutation Testing

Table 11. Saving Obtained by Selective Mutation

Program	No. of Strong Mutants	No. of 2-Selective Mutants	Percentage Saved by 2-Selective Mutation	No. of 4-Selective Mutants	Percentage Saved by 4-Selective Mutation	No. of 6-Selective Mutants	Percentage Saved by 6-Selective Mutation
Banker	2765	1944	29.69	1546	44.09	1186	57.11
Bub	338	277	18.05	224	33.73	197	41.71
Cal	3010	2472	17.87	1804	33.72	738	75.48
Euclid	196	142	27.56	119	40.07	119	40.07
Find	1022	622	39.15	525	39.29	505	50.59
Insert	460	352	23.48	276	48.63	206	55.22
Mid	183	133	27.32	133	27.32	133	27.32
Quad	359	1279	22.28	212	40.95	200	44.29
Trityp	951	810	14.83	579	39.12	533	43.95
Warshall	305	259	15.08	205	32.79	162	46.89
Total	9589	7290	23.98	5623	41.36	3782	60.56

2-selective mutation obtained an average saving of 23.98% and the highest saving at 39.15% for FIND. 4-selective mutation obtained an average saving of 41.36%. The highest saving was 48.63% from INSERT. 6-selective mutation obtained an average saving of 60.56%. The highest saving was 75.48% from CAL. Since selective mutation testing can achieve a saving that exceeds 60% without affecting the effectiveness of test sets, it seems to be a very good alternative to strong mutation testing.

5.2 Effectiveness of Selective Mutation Testing

Fig 7. Distribution of Mutation Operators [5]

In Offutt et al's experiment, they generated test sets that are 100% mutation adequate for 2-selective mutation. The test sets were later applied to strong mutation testing. The averaged results from 5 different test sets are shown in Table 12.

Table 12. Strong Mutation Scores Achieved by 2-Selective Mutation Test Sets

Program	Test Cases	Number of Live Mutants	Strong Mutation Score
Banker	57.4	0	1.00
Bub	7.2	0	1.00
Cal	50.0	0	1.00
Euclid	3.8	0	1.00
Find	14.6	0.6	0.9994
Insert	3.8	0	1.00
Mid	25.2	0	1.00
Quad	12.2	0	1.00
Trityp	44.6	0.2	0.9998
Warshall	7.2	0	1.00
Average	22.6	0.1	0.9999

The test sets that were 100% adequate for 2-selective mutation were almost 100% adequate for strong mutation. In fact, eight out of the ten 2-selective test sets were 100% adequate for strong mutation. The 2-selective mutation test sets achieve high scores on strong mutation testing because the mutants generated by the two operators omitted can be easily killed by tests from other types of mutants [5]. Offutt further extended the experiment by performing 4-selective and 6-selective mutation testing. The four operators omitted in 4-selective mutation testing were SVR, ASR, CSR, and SCR. The six mutation operators omitted in 6-selective mutation testing were ASR, CSR, SCR, SVR, ARC, and ACR. The averaged results from 5 different test sets are shown in Table 13 and Table 14.

Table 13. Strong Mutation Scores Achieved by 4-Selective Mutation Test Sets

Program	Test Cases	Number of Live Mutants	Strong Mutation Score
Banker	38.4	0.2	0.9999
Bub	606	0	1.00
Cal	31.4	0.8	0.9997
Euclid	2.4	2.2	0.9872
Find	13.2	0	1.00
Insert	5.0	0	1.00
Mid	24.8	0	1.00
Quad	10.2	0	1.00
Trityp	44.8	2.0	0.9976
Warshall	7.4	0	1.00
Average	18.4	0.5	0.9984

Table 14. Strong Mutation Scores Achieved by 6-Selective Mutation Test Sets

Program	Test Cases	Number of Live Mutants	Strong Mutation Score
Banker	28.4	1.2	0.9996
Bub	6.6	0	1.00
Cal	26.0	5.2	0.9981
Euclid	2.8	1.8	0.9895
Find	13.4	2.2	0.9977
Insert	4.0	0	1.00
Mid	24.8	0	1.00
Quad	10.0	2.0	0.9939
Trityp	39.8	0	1.00
Warshall	4.2	2.0	0.9926
Average	160	1.4	0.9971

The 2-selective test sets had an average of 99.99%; the 4-selective mutation test sets had an average of 99.84%; the 6-selective test sets had 99.71%. The lowest score for 2-selective was 99.94%; the lowest for 4-selective was 99.72%; the lowest for 6-selective was 98.95%. The results from the three selective mutation test sets were not significantly different. However, they reduced the cost by a wide margin.

6. Conclusion

Mutation testing is a powerful error-based testing technique. Test sets, generated by applying simple syntactic modifications to a program, guarantee those simple errors are absent from the program up to certain confidence level. The confidence level is quantified by the mutation score. Mutation testing has several advantages that cannot be compared by other testing methods: it offers more test coverage; it detects more faults [3]; it can be applied to non-procedural programs, as well as a wide variety of programming languages and styles [6]. However, mutation testing suffers from expensive computational cost. Variations such as weak mutation, firm mutation, and selective mutation testing, have been proposed to combat the problem. Strong, weak, firm, and selective mutation testing are studied in this paper. The effectiveness of the variations is compared in terms of mutation score. The savings are compared in terms of the number of mutants or test cases generated. A summary of their performances is presented in Table 15 and Table 16.

Table 15. Strong Mutation Scores of Various Mutation Testing Methods

	Weak Mutation				Selective Mutation
	EX-WEAK/1	ST-WEAK/1	BB-WEAK/1	BB-WEAK/N	2-Selective	4- elective	6-Selective
Banker	-	-	-	-	1.00	0.9999	0.9996
Bub	0.986	0.994	0.993	0.99	1.00	1.00	1.00
Cal	0.976	0.992	0.99	0.982	1.00	0.9997	0.9981
Euclid	0.998	0.998	0.9975	0.99	1.00	0.9872	0.9895
Find	0.972	0.98	0.982	0.972	0.9994	1.00	0.9977
Insert	1.00	1.00	1.00	1.00	1.00	1.00	1.00
Mid	0.9675	1.00	1.00	1.00	1.00	1.00	1.00
Quad	0.989	1.00	1.00	1.00	1.00	1.00	0.9939
Trityp	-	0.948	0.955	-	0.9998	0.9976	1.00
Warshall	-	-	-	-	1.00	1.00	0.9926
Average	0.984	0.99	0.99	0.99	0.9999	0.9984	0.9971

Table 16. The Number of Mutants Generated for Various Mutation Methods

	Strong	Weak	Selective Mutation
	Mutation	Mutation	2-Selective	4-Selective	6-Selective
Banker	2765	-	1944	1546	1186
Bub	338	338	277	224	197
Cal	3010	3009	2472	1804	738
Euclid	196	195	142	119	119
Find	1022	1022	622	525	505
Insert	460	460	352	276	206
Mid	183	183	133	133	133
Quad	359	359	1279	212	200
Trityp	951	951	810	579	533
Warshall	305	305	259	205	162

Firm mutation testing can be seen as an extension of weak mutation testing. Its cost and effectiveness have yet to be determined empirically. From Table 15 and 16, selective mutation testing is found to perform better than weak mutation testing in terms of both mutation scores and computational savings. Of the four weak mutation methods, ST-WEAK/1 seemed to achieve the highest mutation score but had the highest computational cost. 2-selective mutation gives the best mutation scores of the three selective mutation methods, but it has the least computational saving. A trade off exists between effectiveness and computational saving. Testers can choose the most appropriate method for a program according their desired confidence level and the available resources.

7. References

1. R. A. DeMillo, R. J. Lipton, and F. G. Sayward. Hints on Test Data Selection: Help for the Practicing Programmer. IEEE Computer, 11(4):34-41, April 1978.
2. A. J. Offutt, and Ss. D. Lee. An Empirical Evaluation of Weak Mutation. IEEE Transactions on Software Engineering, vol. 20, no. 5, 337-344, May 1994.
3. A. J. Offutt, J. Pan, K. Tewary, and T. Zhang. An Experimental Evaluation of Data Flow and Mutation Testing. Software-Practice and Experience, vol. 26(2): 165-176, February 1996.
4. R. A. DeMillo, D. S. Guindi, W. M. McCracken, A. J. Offutt, and K. N. King. An Extended Overview of the Mothra Software Testing Environment. IEEE Proceedings of Second Workshop on Software Testing, Verification, and Analysis, 142-151, July 1988.
5. A. J. Offutt, G. Rothermel, and C. Zapf. An Experimental Evaluation of Selective Mutation. International Conference on Software Engineering, 1993. 100-107. 1993.
6. M. R. Woodward. Mutation Testing - An Evolving Technique. IEE Colloquium on Software Testing for Critical Systems. No. 108. 3/1-3/6. 1990.
7. W. E. Howden. Weak Mutation Testing and Completeness of Test Sets. IEEE Transactions of Software Engineering, vol. SE-8, No. 4, 371-379, July 1982.
8. W. E. Howden. Reliability of the Path Analysis Testing Strategy. IEEE Transactions of Software Engineering, vol. SE-2, 1976.
9. E. J. Weyuker and T. J. Ostrand. Theories of Program Tesing and the Application of Revealing Subdomains. IEEE Transactios of Software Engineering, vol. SE-6, 1980.
10. A. P. Mathur. Performance, Effectiveness, and Reliability Issues in Software Testing. IEEE Proceedings of 15^th Annual International Computer Software & Application Conference. 604-605, 1991.
11. T. A. Budd. Mutation Analysis of Program Test Data. PhD thesis, Yale University, New Haven CT, 1980.
12. A. T. Acree, T. A. Budd, R. A. DeMillo, R. J. Lipton, and F. G. Sayward. Mutation Analysis. Technical report GIT-ICS-79/08, School of Information and Computer Science, Georgia Institute of Technology, Atlanta GA, September 1979.
13. M. R. Woodward, K. Halewood. From Weak To Strong, Dead Or Alive?? An Analysis of Some Mutation Testing Issues. IEEE Proceedings of Second Workshop on Software Testing, Verification, and Analysis, 152-158, July 1988.
14. A. J. Offutt. Investigations of the Software Testing Coupling Effect. ACM Transactions on Software Engineering and Methodology, Vol. 1, No. 1, 5-20, January 1992.